הבדלים בין גרסאות בדף "אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות"
(←שאלה - o, גבולות) |
(←שאלות) |
||
| שורה 69: | שורה 69: | ||
ולכן הטענה נכונה. | ולכן הטענה נכונה. | ||
| + | ==שאלה בתרגיל 3 1== | ||
| + | האם שטח מינימלי יכול להיות 0? זאת אומרת שהמשולש יהיה בעצם נקודה. | ||
גרסה מ־17:47, 22 במרץ 2010
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
ארכיון
שאלות
שאלות
היי, (הוספתי שאלה למעלה באחד הדיונים מדוע המונה - Rn(x)- שואף ל0 לאחר גזירות מסוימות..)
- ונתנה לכך תשובה, תסתכל בארכיון.
- אבל ניתנה תשובה רק לשלב הראשון. הסתבכתי קצת עם הגזירה הראשונה. תוכל בבקשה להראות רק את השלב של הגזירה הראשונה ולהסביר למה עדיין יוצא שהמונה שואף ל0?
תשובה
השארית הינה:
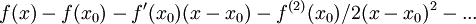 ולכן הנגזרת של זה הינה
ולכן הנגזרת של זה הינה
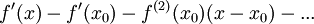
והטענה דומה
- למה בגזירה, כתבת את הנגזרת השניה של x-x0 ולא את הנגזרת השניה של X?
- שגיאת דפוס.... תיקנתי.
- רגע, אבל זה לא ביטוי מורכב? כלומר, f'(x) כפול ביטוי שהוא x-x0? לא אמור לגזור את זה לפי (u*g)' = u'+g' ?
- שגיאת דפוס.... תיקנתי.
- למה בגזירה, כתבת את הנגזרת השניה של x-x0 ולא את הנגזרת השניה של X?
- לא,
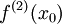 הוא קבוע כי
הוא קבוע כי  קבוע!. x הינו משתנה, ואנחנו גוזרים לפיו.
קבוע!. x הינו משתנה, ואנחנו גוזרים לפיו.
- (סליחה על החפירה), לא ממש הצלחתי להבין.. יש לנו את הביטוי f'(x0)*(x-x0), אם f'(x0) הוא קבוע אז למה בגזירה הביטוי הופך לf(2)(x0)? ולמה x-x0 נשאר כמו שהוא?
- לא,
זה לא מה שקרה. את 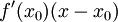 גזרנו לפי x (זה לא ביטוי קבוע) וקיבלנו
גזרנו לפי x (זה לא ביטוי קבוע) וקיבלנו 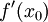 שזה המקדם של x.
שזה המקדם של x.
את 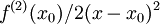 גזרנו לקבל
גזרנו לקבל 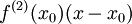
תחשוב, איך היית גוזר את הפונקציה 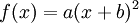 ?
?
- הבנתי, תודה רבה.
שאלה
יש לי שאלה נוספת. בהגדרה של קמירות כלפי מטה ומעלה, האם מדובר על סביבה מנוקבת של x0? כי בהגדרה אצלנו יש אי שיוויון ממש של h(x)>f(x) או h(x)<f(X), כלומר לא כוללים את x0 בסביבה, נכון? (אחרת זה לא היה גדול ממש או קטן ממש, אלא גדול שווה/קטן שווה.)
- אני חושב שאתה צודק. המטרה של האי שיוויון היא שנקודה בפונקציה קבועה לא תהיה נקודת פיתול (אבל היא כן נקודת קיצון)
תרגיל 2 - שאלה 3a
האם מותר לי להגדיר פונקצייה חדשה שהיא ההפרש בין שתי הפונקציות, ולפתח אותה לפי טיילור סביב הנק' x0, ואז להראות שאני יכול לבחור כל x שגדול מ- כדי לקבל שערך הפונקצייה החדשה חיובי תמיד (ומכאן להסיק שאחת מהפונקציות גדולה מהשנייה)? כלומר, שלכל
כדי לקבל שערך הפונקצייה החדשה חיובי תמיד (ומכאן להסיק שאחת מהפונקציות גדולה מהשנייה)? כלומר, שלכל 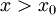 שאני אבחר קיים c מתאים שעבורו זה מתקיים, לכן זה מתקיים לכל x כזה. האם מותר לי לומר את זה?
שאני אבחר קיים c מתאים שעבורו זה מתקיים, לכן זה מתקיים לכל x כזה. האם מותר לי לומר את זה?
- לא מבין את מטרת השאלה.
- האם הרעיון לפתרון התרגיל, ואופן הביצוע שלו נכון (כפי שתיארתי כאן)? כי שמעתי מהרבה שהם עשו את התרגיל בדרך שונה לגמרי.
- כל דרך שאכן מוכיחה היא טובה, על מנת לדעת אם התשובה היא טובה יש בדיקת תרגילים ופרסום פתרונות. בגדול מה שרשמת זה אכן נכון, כמובן נדרש פירוט מדוייק...
- תודה רבה :) !!
שאלה - o, גבולות
1. הביטוי 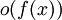 כש-x שואף לערך מסוים בעצם מסמל ביטוי שזניח ביחס ל-
כש-x שואף לערך מסוים בעצם מסמל ביטוי שזניח ביחס ל- , במילים אחרות, נכון?
, במילים אחרות, נכון?
2. נניח שיש לי ביטוי שעבור x ששואף לערך מסוים הוא 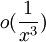 , ואני כופל אותו ב-
, ואני כופל אותו ב- , האם הוא הופך להיות
, האם הוא הופך להיות 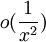 ?
?
תשובה
1. כן
2. קל לבדוק לפי ההגדרה. נניח f הינה 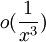 . ולכן לפי הגדרה:
. ולכן לפי הגדרה:
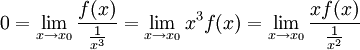
ולכן הטענה נכונה.
שאלה בתרגיל 3 1
האם שטח מינימלי יכול להיות 0? זאת אומרת שהמשולש יהיה בעצם נקודה.