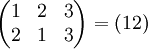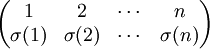הבדלים בין גרסאות בדף "תמורה"
מתוך Math-Wiki
| שורה 1: | שורה 1: | ||
| + | ==הגדרה== | ||
תהי <math>A=\{1,2,...,n\}</math> '''תמורה''' הינה פונקציה חח"ע ועל מA לA | תהי <math>A=\{1,2,...,n\}</math> '''תמורה''' הינה פונקציה חח"ע ועל מA לA | ||
| + | |||
| + | '''מחזור''' <math>\sigma=(a_1 a_2 ... a_n)</math> הוא תמורה המקיימת: | ||
| + | :לכל <math>i<k</math> מתקיים <math>\sigma(a_i)=a_{i+1}</math> | ||
| + | :<math>\sigma(a_k)=a_1</math> | ||
| + | :לכל <math>n\in A</math> כך שלכל i <math>n\neq a_i</math> אזי <math>\sigma(n)=n</math> | ||
| + | |||
| + | |||
| + | נהוג לסמן תמורה באופן הבא, או כהרכבה של מחזורים. | ||
| + | |||
| + | :<math>\begin{pmatrix} 1 & 2 & \cdots & n \\ \sigma(1) & \sigma(2) & \cdots & \sigma(n)\end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==דוגמאות== | ||
| + | ניקח <math>A=\{1,2,3\}</math>, והאת התמורה המחליפה בין 1 לבין 2. ניתן לסמן אותה באופנים הבאים: | ||
| + | |||
| + | <math>\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3\end{pmatrix}=(1 2)</math> | ||
גרסה מ־19:13, 5 באפריל 2012
הגדרה
תהי  תמורה הינה פונקציה חח"ע ועל מA לA
תמורה הינה פונקציה חח"ע ועל מA לA
מחזור 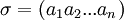 הוא תמורה המקיימת:
הוא תמורה המקיימת:
- לכל
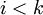 מתקיים
מתקיים 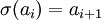
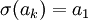
- לכל
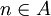 כך שלכל i
כך שלכל i 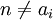 אזי
אזי 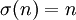
נהוג לסמן תמורה באופן הבא, או כהרכבה של מחזורים.
דוגמאות
ניקח 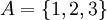 , והאת התמורה המחליפה בין 1 לבין 2. ניתן לסמן אותה באופנים הבאים:
, והאת התמורה המחליפה בין 1 לבין 2. ניתן לסמן אותה באופנים הבאים: