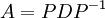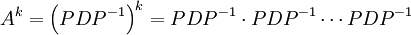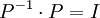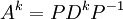הבדלים בין גרסאות בדף "לכסון מטריצה"
מתוך Math-Wiki
(יצירת דף עם התוכן "'''הגדרה:''' תהי A מטריצה ריבועית. אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה...") |
|||
| שורה 2: | שורה 2: | ||
אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה]] למטריצה אלכסונית | אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה]] למטריצה אלכסונית | ||
| + | |||
| + | |||
| + | '''משפט.''' | ||
| + | |||
| + | תהי <math>A\in\mathbb{F}^{n\times n}</math> מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב <math>\mathbb{F}^n</math> כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A. | ||
| + | |||
| + | |||
| + | '''הוכחה.''' | ||
| + | |||
| + | |||
==דוגמא חשובה לשימוש בלכסינות== | ==דוגמא חשובה לשימוש בלכסינות== | ||
גרסה מ־11:48, 25 באוקטובר 2012
הגדרה: תהי A מטריצה ריבועית.
אומרים כי A מטריצה לכסינה אם היא דומה למטריצה אלכסונית
משפט.
תהי 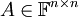 מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב
מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב 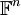 כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A.
כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A.
הוכחה.
דוגמא חשובה לשימוש בלכסינות
באמצעות לכסון ניתן למצוא חזקות גבוהות של מטריצות באופן הבא. נניח A מטריצה לכסינה, לכן קיימת מטריצה אלכסונית D ומטריצה הפיכה P כך שמתקיים:
ולכן
אבל
לכן סה"כ אנחנו מקבלים
כאשר להעלות מטריצה אלכסונית בחזקה זה קל מאד.