הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/תרגילים/תרגיל 1"
מתוך Math-Wiki
עופר בוסאני (שיחה | תרומות) |
|||
| שורה 4: | שורה 4: | ||
הוכיחו: <math>m^*(aE+b)=|a| m^*(E)</math> | הוכיחו: <math>m^*(aE+b)=|a| m^*(E)</math> | ||
== שאלה 2 == | == שאלה 2 == | ||
| − | + | הוכיחו כי כל קבוצה קומפקטית הינה מדידה. | |
| − | + | ||
| − | + | ||
| − | + | ||
== שאלה 3 == | == שאלה 3 == | ||
'''הגדרה:''' נאמר שקבוצה <math>G \subseteq \mathbb{R}</math> היא מטיפוס <math>G_\delta</math> אם ניתן להציג אותה כחיתוך בן-מנייה של קבוצות פתוחות. | '''הגדרה:''' נאמר שקבוצה <math>G \subseteq \mathbb{R}</math> היא מטיפוס <math>G_\delta</math> אם ניתן להציג אותה כחיתוך בן-מנייה של קבוצות פתוחות. | ||
גרסה מ־08:32, 20 באוקטובר 2013
שאלה 1
לכל קבוצה 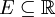 ומספרים
ומספרים 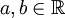 מגדירים
מגדירים 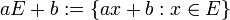 (ז"א ש-
(ז"א ש-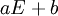 היא תמונת
היא תמונת  תחת הפונקציה הלינארית
תחת הפונקציה הלינארית 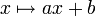 ).
).
הוכיחו: 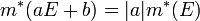
שאלה 2
הוכיחו כי כל קבוצה קומפקטית הינה מדידה.
שאלה 3
הגדרה: נאמר שקבוצה 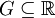 היא מטיפוס
היא מטיפוס 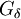 אם ניתן להציג אותה כחיתוך בן-מנייה של קבוצות פתוחות.
אם ניתן להציג אותה כחיתוך בן-מנייה של קבוצות פתוחות.
תהי 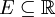 הוכיחו שקיימת קבוצה
הוכיחו שקיימת קבוצה 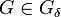 המקיימת
המקיימת 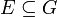 וכן
וכן 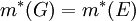
הדרכה: עקבו אחרי השלבים הבאים:
א. הוכיחו שלכל קבוצה 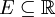 ולכל
ולכל  קיימת קבוצה פתוחה
קיימת קבוצה פתוחה 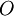 , המקיימת
, המקיימת 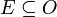 וכן
וכן
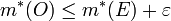
ב. בנו סדרה של קבוצות פתוחות מתאימות ע"פ א' וחיתכו אותן.
בהצלחה!