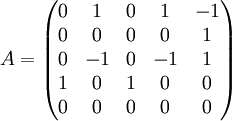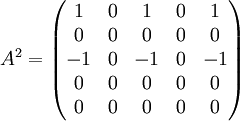הבדלים בין גרסאות בדף "משפט ז'ורדן"
מתוך Math-Wiki
(←דוגמאות) |
(←דוגמאות) |
||
| שורה 38: | שורה 38: | ||
*שנית, נמצא את הפולינום המינימלי <math>m_A(x)=x^3</math>, בפרט המטריצה ניליפוטנטית מסדר 3 | *שנית, נמצא את הפולינום המינימלי <math>m_A(x)=x^3</math>, בפרט המטריצה ניליפוטנטית מסדר 3 | ||
| − | *כעת נמצא בסיס ל <math> | + | *כעת נמצא בסיס ל <math>C(A^{3-1})</math> מהצורה <math>A^2v_1,A^2v_2,...,A^2v_k</math> באופן הבא: |
| + | **נבחר עמודות של המטריצה <math>A^2</math> המהוות בסיס ל- <math>C(A^2)</math> | ||
| + | **כל עמודה i שבחרנו ניתן להציג כ- <math>A^2e_i</math> | ||
| שורה 50: | שורה 52: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | לכן בסיס למרחב העמודות הינו <math>A^2e_1</math> | ||
| + | |||
| + | *כעת המסלול <math>A^2e_1,Ae_1,e_1</math> הוא חלק של הבסיס המז'רדן '''משמאל לימין'''. שימו לב שסדר הוקטורים בבסיס המז'רדן חשוב מאד. | ||
גרסה מ־12:22, 3 בדצמבר 2012
תוכן עניינים
בלוק ז'ורדן
בלוק ז'ורדן הינו מטריצה ריבועית מהצורה
לדוגמא,
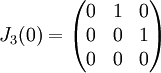 ,
, 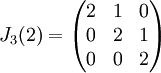
נזכר בסימון של סכום ישר של מטריצות, לדוגמא:
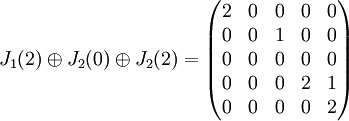
משפט ז'ורדן
תהי A מטריצה ריבועית, כך שהפולינום האופייני שלה מתפרק לגורמים לינאריים. אזי A דומה למטריצה אלכסונית בלוקים, כאשר כל בלוקיה הם בצורת ג'ורדן. בנוסף, צורה זו יחידה עד כדי סדר הבלוקים.
הוכחה ומציאת מטריצה מז'רדנת
סיכום בנושא משפט ז'ורדן על ידי דר' בועז צבאן
דוגמאות
מצא בסיס מז'רדן למטריצה הבאה:
- ראשית, נחשב את הפולינום האופייני
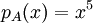 , כלומר זוהי מטריצה ניליפוטנטית
, כלומר זוהי מטריצה ניליפוטנטית
- שנית, נמצא את הפולינום המינימלי
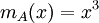 , בפרט המטריצה ניליפוטנטית מסדר 3
, בפרט המטריצה ניליפוטנטית מסדר 3
- כעת נמצא בסיס ל
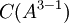 מהצורה
מהצורה 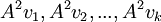 באופן הבא:
באופן הבא:
- נבחר עמודות של המטריצה
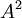 המהוות בסיס ל-
המהוות בסיס ל- 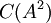
- כל עמודה i שבחרנו ניתן להציג כ-
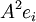
- נבחר עמודות של המטריצה
לכן בסיס למרחב העמודות הינו 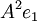
- כעת המסלול
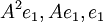 הוא חלק של הבסיס המז'רדן משמאל לימין. שימו לב שסדר הוקטורים בבסיס המז'רדן חשוב מאד.
הוא חלק של הבסיס המז'רדן משמאל לימין. שימו לב שסדר הוקטורים בבסיס המז'רדן חשוב מאד.