הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/תרגילים/תרגיל 6"
(יצירת דף עם התוכן "== שאלה 0 (לא להגשה) == קראו בויקיפדיה על [http://he.wikipedia.org/wiki/%D7%A4%D7%95%D7%A0%D7%A7%D7%A6%D7%99%D7%99%D7%AA_%D7%A7%D7%A0%D7%9...") |
(←שאלה 1) |
||
| שורה 6: | שורה 6: | ||
יהי <math>(X,\mathcal{S},\mu)</math> ממ"ח, <math>f:X \to [0,\infty]</math> מדידה ואי-שלילית, ומקיימת <math>\int_X f \, d\mu=c</math> באשר <math>0<c<\infty</math>. יהי <math>\alpha>0</math> קבוע. | יהי <math>(X,\mathcal{S},\mu)</math> ממ"ח, <math>f:X \to [0,\infty]</math> מדידה ואי-שלילית, ומקיימת <math>\int_X f \, d\mu=c</math> באשר <math>0<c<\infty</math>. יהי <math>\alpha>0</math> קבוע. | ||
| − | הוכיחו כי מתקיים <math>\lim_{n \to \infty} \int_X {n \log \left[ 1+\left( \frac{f}{n} \right)^\alpha \right]}=\begin{cases} \infty & 0<\alpha<1 \\ c & \alpha=1\\ 0 & 1<\alpha <\infty \end{cases}</math> | + | הוכיחו כי מתקיים <math>\lim_{n \to \infty} \int_X {n \log \left[ 1+\left( \frac{f}{n} \right)^\alpha \right]} \, d\mu=\begin{cases} \infty & 0<\alpha<1 \\ c & \alpha=1\\ 0 & 1<\alpha <\infty \end{cases}</math> |
'''רמז:''' אם <math>\alpha \ge 1</math>, האינטגרנדים נשלטים ע"י <math>\alpha f</math>, | '''רמז:''' אם <math>\alpha \ge 1</math>, האינטגרנדים נשלטים ע"י <math>\alpha f</math>, | ||
ואם <math>\alpha<1</math> ניתן להפעיל את למת פאטו. | ואם <math>\alpha<1</math> ניתן להפעיל את למת פאטו. | ||
| − | |||
== שאלה 2 == | == שאלה 2 == | ||
גרסה אחרונה מ־21:53, 6 בדצמבר 2012
תוכן עניינים
שאלה 0 (לא להגשה)
קראו בויקיפדיה על פונקציית קנטור, ועל הדרך שבעזרתה בונים קבוצת לבג שאיננה קבוצת בורל (ובעצם מוכיחים ש-  ).
).
שאלה 1
יהי 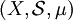 ממ"ח,
ממ"ח, ![f:X \to [0,\infty]](/images/math/2/f/b/2fb58d8cc01c5a0e217aedffdc6507b3.png) מדידה ואי-שלילית, ומקיימת
מדידה ואי-שלילית, ומקיימת 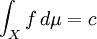 באשר
באשר 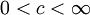 . יהי
. יהי 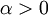 קבוע.
קבוע.
הוכיחו כי מתקיים ![\lim_{n \to \infty} \int_X {n \log \left[ 1+\left( \frac{f}{n} \right)^\alpha \right]} \, d\mu=\begin{cases} \infty & 0<\alpha<1 \\ c & \alpha=1\\ 0 & 1<\alpha <\infty \end{cases}](/images/math/0/2/e/02e28db407c9a0af4e41a5b429207631.png)
רמז: אם 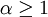 , האינטגרנדים נשלטים ע"י
, האינטגרנדים נשלטים ע"י 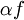 ,
,
ואם 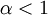 ניתן להפעיל את למת פאטו.
ניתן להפעיל את למת פאטו.
שאלה 2
יהי 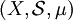 ממ"ח, ותהי
ממ"ח, ותהי ![f:X \to [0,\infty]](/images/math/2/f/b/2fb58d8cc01c5a0e217aedffdc6507b3.png) מדידה
מדידה 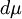 . עבור
. עבור  נגדיר
נגדיר 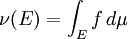 . הוכחנו בהרצאה כי
. הוכחנו בהרצאה כי 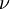 היא מידה.
היא מידה.
א. הוכיחו כי לכל ![g:X \to [0,\infty]](/images/math/2/a/e/2aeb42da80af17a04ac2498d65581937.png) מדידה
מדידה 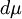 מתקיים
מתקיים 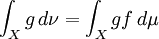 .
.
(הדרכה: הראו זאת בשלבים כמו בתרגיל הקודם - התחילו מפונקציית אינדיקטור, וסיימו בפונקציה אי-שלילית כללית)
ב. באיזה תנאי פונקציה  אינטגרבילית
אינטגרבילית 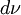 ?
?
שאלה 3
יהי  ממ"ח בו
ממ"ח בו 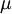 היא מידת הספירה. פונקציות
היא מידת הספירה. פונקציות  הן בעצם סדרות של מספרים ממשיים.
הן בעצם סדרות של מספרים ממשיים.
א. תהיינה  הפונקציות המוגדרות ע"י
הפונקציות המוגדרות ע"י  . מי מהן מדידה? מי מהן אינטגרבילית? חשבו את האינטגרל של האינטגרבילית מביניהן.
. מי מהן מדידה? מי מהן אינטגרבילית? חשבו את האינטגרל של האינטגרבילית מביניהן.
ב. תנו אפיון (תנאי הכרחי ומספיק) של הפונקציות המדידות 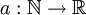 .
.
ג. כנ"ל עבור הפונקציות האינטגרביליות.
ד. מצאו ביטוי לאינטגרל של פונקציה אינטגרבילית 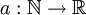 .
.
(שימו לב שתאריך ההגשה הוא בשבוע שלאחר חנוכה)
בהצלחה!