הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5"
אחיה בר-און (שיחה | תרומות) (←עיקרון הסדר הטוב) |
אחיה בר-און (שיחה | תרומות) (←עיקרון הסדר הטוב) |
||
| שורה 68: | שורה 68: | ||
אזי אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר מינימום בקבוצה. | אזי אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר מינימום בקבוצה. | ||
| + | |||
| + | |||
| + | דוגמא נוספת: | ||
| + | |||
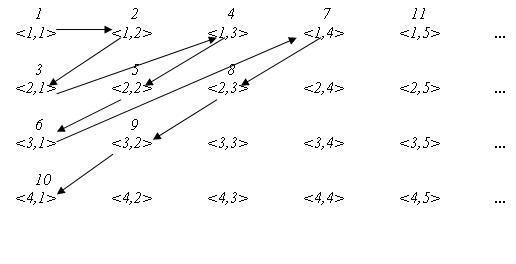
| + | ניתן להגדיר אל <math>\mathbb{Q}_+</math> יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות) | ||
| + | |||
| + | [[קובץ:NutualSquareEqNutural.jpeg]] | ||
| + | |||
| + | התבוננו והשתכנעו שזה גם סדר טוב. | ||
| + | |||
| + | הערה: זה בניגוד לסדר "קטן שווה" הרגיל על השברים שאינו סדר טוב כי לקבוצה | ||
| + | <math>\{x\in \mathbb{Q}_+ | x<\sqrt{2}\}</math> אין איבר מינימום. | ||
==הכללות== | ==הכללות== | ||
גרסה מ־12:26, 17 ביולי 2014
תוכן עניינים
רעיון בסיסי - אינדוקציה על הטבעיים
בשביל להוכיח שטענה מסוימת 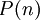 נכונה עבור כל מספר טבעי
(למשל
נכונה עבור כל מספר טבעי
(למשל 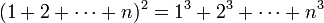 ) מספיק להוכיח את הבאים:
) מספיק להוכיח את הבאים:
- (בסיס האינדוקציה) הטענה מתקיימת עבור
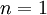 כלומר
כלומר 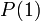 מתקיים
מתקיים - (צעד האינדוקציה)אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
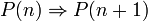 .
.
למה זה מספיק?
בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור 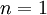 כלומר
כלומר 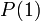 מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור
מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור 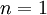 (שזה אכן כך) אז הטענה נכונה גם עבור
(שזה אכן כך) אז הטענה נכונה גם עבור 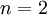 כלומר
כלומר 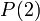 . אה! אז עכשיו זה נכון עבור
. אה! אז עכשיו זה נכון עבור 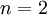 אז לפי אותה טענה זה נכון גם עבור
אז לפי אותה טענה זה נכון גם עבור 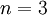 ! ומה עכשיו? אם זה נכון עבור
! ומה עכשיו? אם זה נכון עבור 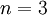 זה נכון עבור
זה נכון עבור 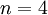 . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר
. וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר 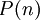 נכון לכל
נכון לכל 
דוגמא:
נוכיח באינדוקציה כי הטענה 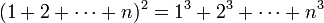 נכונה לכל
נכונה לכל 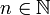 טבעי
טבעי
הוכחה:
עבור 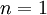 אכן מתקיים כי
אכן מתקיים כי 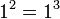
כעת נניח כי הטענה עבור  כלשהוא, כלומר מתקיים
כלשהוא, כלומר מתקיים
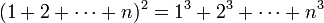 ונוכיח כי הטענה נכונה עבור
ונוכיח כי הטענה נכונה עבור 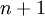 , כלומר
, כלומר
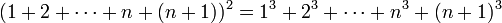
נוכיח
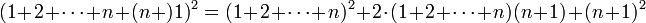
לפי הנחת האינדוקציה אפשר להמשיך הלאה
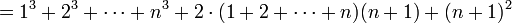
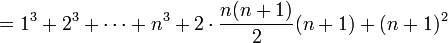
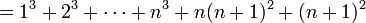
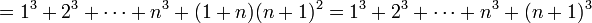
וסיימנו
דוגמא נוספת:
הוכח כי לכל מספר טבעי  מתקיים כי
מתקיים כי 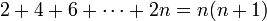
פתרון:
עבור 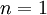 אכן מתקיים
אכן מתקיים 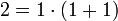
כעת נניח שהטענה נכונה עבור  ונוכיח את הטענה עבור
ונוכיח את הטענה עבור 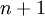
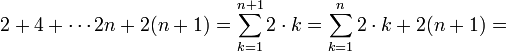
לפי הנחת האינדוקציה ניתן להמשיך
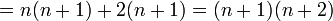
שזה הטענה עבור 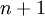 וסיימנו.
וסיימנו.
עיקרון הסדר הטוב
הגדרה:
תהא  קבוצה עם יחס סדר חלקי
קבוצה עם יחס סדר חלקי 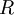 על
על  .
.
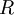 יקרא סדר טוב אם לכל
יקרא סדר טוב אם לכל 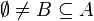 קיים איבר מינימום/הכי קטן/ראשון ב
קיים איבר מינימום/הכי קטן/ראשון ב  .
.
דוגמא (אינטואיטיבית):
נסתכל על 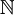 קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי.
קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי.
אזי אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר מינימום בקבוצה.
דוגמא נוספת:
ניתן להגדיר אל 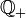 יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות)
יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות)
התבוננו והשתכנעו שזה גם סדר טוב.
הערה: זה בניגוד לסדר "קטן שווה" הרגיל על השברים שאינו סדר טוב כי לקבוצה
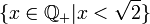 אין איבר מינימום.
אין איבר מינימום.
הכללות
הכללה פשוטה 1
הכללה ישירה מתבצעת כך (החלפה רק של הטענה הראשונה): אם נוכיח עבור טענה 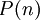 ש:
ש:
- הטענה מתקיימת עבור
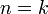 מסוים כלומר
מסוים כלומר 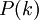 מתקיים
מתקיים - אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
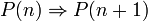 .
.
אז באופן דומה הטענה נכונה 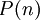 נכונה עבור
נכונה עבור 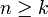
כלומר - במקום להוכיח עבור 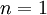 ואז הטענה מתקיים החל מ-1 ניתן להוכיח עבור
ואז הטענה מתקיים החל מ-1 ניתן להוכיח עבור 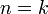 ואז הטענה מתקיים החל מ-k
ואז הטענה מתקיים החל מ-k
דוגמא:
הוכח כי לכל 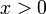 מתקיים
מתקיים 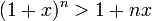 לכל
לכל 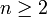
פתרון:
עבור 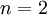 נקבל
נקבל 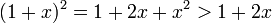 כי
כי 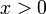
כעת נניח כי הטענה נכונה עבור  כלשהוא, כלומר מתקיים
כלשהוא, כלומר מתקיים 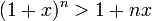
נוכיח עבור 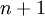 מהנחת האינדוקציה נקבל כי
מהנחת האינדוקציה נקבל כי
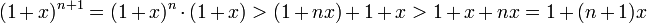
וסיימנו
הכללה פשוטה 2
אם נוכיח עבור טענה 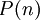 ש:
ש:
- הטענה מתקיימת עבור
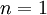 מסוים כלומר
מסוים כלומר 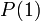 מתקיים
מתקיים - אם הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים
 (כלומר מתקיים
(כלומר מתקיים 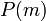 עבור
עבור 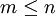 ) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר
) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר 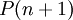 מתקיים).
מתקיים).
אז באופן דומה הטענה נכונה 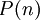 נכונה עבור
נכונה עבור 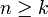
כלומר - אפשר להחליף את ההנחה שמתקיים עבור  ולהוכיח עבור
ולהוכיח עבור 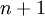 בהנחה שמתקיים עבור כל מי שקטן שווה
בהנחה שמתקיים עבור כל מי שקטן שווה  ולהוכיח עבור
ולהוכיח עבור 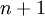
דוגמא:
כל מספר טבעי 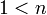 ניתן להציגו כמכפלה של מספרים ראשוניים
ניתן להציגו כמכפלה של מספרים ראשוניים
הוכחה:
עבור 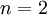 זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
כעת נניח שהטענה נכונה לכל 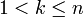 ונוכיח עבור
ונוכיח עבור 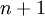
אם 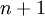 ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
אחרת 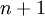 מתפרק למכפלה
מתפרק למכפלה 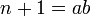 כאשר
כאשר 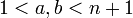 לפי הנחת האינדוקציה
לפי הנחת האינדוקציה 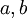 מתפרקים למכפלה של מספרים ראשוניים
מתפרקים למכפלה של מספרים ראשוניים
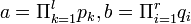 כאשר
כאשר 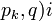 ראשוניים
ראשוניים
ואז 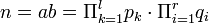
וסיימנו
הכללה מעמיקה
תהא  קבוצה סדורה היטב בת מניה אז אפשר לעשות שם אינדוקציה
קבוצה סדורה היטב בת מניה אז אפשר לעשות שם אינדוקציה
הערה: אפשר לעשות אינדוקציה טרנספניטית על קבוצות כלשהן (לאו דווקא בנות מניה) הערה: קיום סדר טוב על הטבעיים שקול לקיומה של אינדוקציה על הטבעיים.
תרגילים יותר מעניינים
כפל n מטריצות הפרש סימטרי של n קבוצות