הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 11"
מתוך Math-Wiki
אחיה בר-און (שיחה | תרומות) (←הגדרות בסיסיות) |
אחיה בר-און (שיחה | תרומות) (←הגדרות בסיסיות) |
||
| שורה 9: | שורה 9: | ||
| − | דוגמא: <math>V=\{1,2,3\}, E=\ | + | דוגמא: <math>V=\{1,2,3\}, E=\Big\{\{1,2\},\{2,3\},\{1,3\}\Big\}</math> מייצג משולש. |
| − | + | ||
| − | מייצג משולש. | + | |
'''הגדרה''' הסדר של גרף <math>G=(V,E)</math> הוא <math>|V|</math>. גרף יקרא סופי אם הסדר שלו סופי (וגם <math>E</math> סופית) | '''הגדרה''' הסדר של גרף <math>G=(V,E)</math> הוא <math>|V|</math>. גרף יקרא סופי אם הסדר שלו סופי (וגם <math>E</math> סופית) | ||
גרסה מ־08:27, 14 באוגוסט 2014
הגדרות בסיסיות
הגדרה יהיה  קבוצה לא ריקה. יהא
קבוצה לא ריקה. יהא  קבוצה המכילה זוגות לא סדורים מאיברי
קבוצה המכילה זוגות לא סדורים מאיברי  אזי
אזי  נקרא גרף לא מכוון.
נקרא גרף לא מכוון.
חושבים על  כקודקודים של הגרף ועל
כקודקודים של הגרף ועל  כקשתות/צלעות של הגרף. את האיברים ב
כקשתות/צלעות של הגרף. את האיברים ב  נהוג לרשום כקבוצה
נהוג לרשום כקבוצה 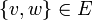 (בגלל שזה זוגות לא סדורים)
(בגלל שזה זוגות לא סדורים)
דוגמא: 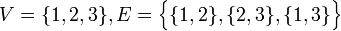 מייצג משולש.
מייצג משולש.
הגדרה הסדר של גרף  הוא
הוא 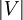 . גרף יקרא סופי אם הסדר שלו סופי (וגם
. גרף יקרא סופי אם הסדר שלו סופי (וגם  סופית)
סופית)
אנחנו נעסוק בגרפים לא מכוונים בלי לולאות כלומר המקיימים 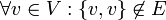
הגדרה יהיה  נאמר כי
נאמר כי 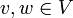 שכנים אם
שכנים אם 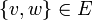 .
.
במקרה זה נאמר כי הצלע 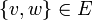 חלה ב
חלה ב 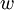 (או חלה ב
(או חלה ב 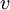 )
)