הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 11"
אחיה בר-און (שיחה | תרומות) (←הגדרות בסיסיות) |
אחיה בר-און (שיחה | תרומות) (←הגדרות בסיסיות) |
||
| שורה 43: | שורה 43: | ||
מעגל הוא מסלול פשוט המקיים <math>v_0=v_n</math> | מעגל הוא מסלול פשוט המקיים <math>v_0=v_n</math> | ||
| − | אורך המסלול <math>(v_0,v_1,\dots,v_n</math> הוא <math>n</math> | + | אורך המסלול <math>(v_0,v_1,\dots,v_n)</math> הוא <math>n</math> |
<math>(v_0,v_1,\dots,v_n)</math> הינו מסלול מ <math>v_0</math> ל <math>v_n</math> | <math>(v_0,v_1,\dots,v_n)</math> הינו מסלול מ <math>v_0</math> ל <math>v_n</math> | ||
גרסה מ־06:49, 18 באוגוסט 2014
הגדרות בסיסיות
הגדרה יהיה  קבוצה לא ריקה. יהא
קבוצה לא ריקה. יהא  קבוצה המכילה זוגות לא סדורים מאיברי
קבוצה המכילה זוגות לא סדורים מאיברי  אזי
אזי  נקרא גרף לא מכוון.
נקרא גרף לא מכוון.
חושבים על  כקודקודים של הגרף ועל
כקודקודים של הגרף ועל  כקשתות/צלעות של הגרף. את האיברים ב
כקשתות/צלעות של הגרף. את האיברים ב  נהוג לרשום כקבוצה
נהוג לרשום כקבוצה 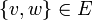 (בגלל שזה זוגות לא סדורים)
(בגלל שזה זוגות לא סדורים)
דוגמא: 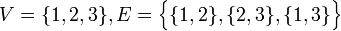 מייצג משולש.
מייצג משולש.
הגדרה הסדר של גרף  הוא
הוא 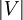 . גרף יקרא סופי אם הסדר שלו סופי (וגם
. גרף יקרא סופי אם הסדר שלו סופי (וגם  סופית)
סופית)
אנחנו נעסוק בגרפים לא מכוונים בלי לולאות כלומר המקיימים 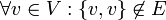 ובלי צלעות כפולות, כלומר לא מופיע פעמיים
ובלי צלעות כפולות, כלומר לא מופיע פעמיים 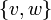 ב
ב  . בנוסף הגרפים שלנו יהיו סופיים.
. בנוסף הגרפים שלנו יהיו סופיים.
הגדרה יהיה  נאמר כי
נאמר כי 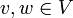 שכנים אם
שכנים אם 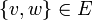 .
.
במקרה זה נאמר כי הצלע 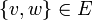 חלה ב
חלה ב 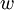 (או חלה ב
(או חלה ב 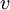 )
)
את קבוצת השכנים של 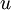 מסמנים כ
מסמנים כ 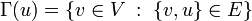
הדרגה של 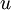 (סימון:
(סימון: 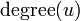 )היא מספר הצלעות החלות ב
)היא מספר הצלעות החלות ב 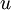 או לחילופין
או לחילופין 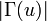
בדוגמא של המשולש - כל 2 קודקודים שכנים. כל קודקוד מדרגה 2. השכנים של קודקוד מספר 1 הוא קודקוד 2 + קודקוד 3.
משפט (לחיצת הידיים)
יהי  גרף לא מכוון. אזי
גרף לא מכוון. אזי 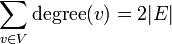 .
.
עוד הגדרות:
יהי  גרף לא מכוון. סדרת קודקודים (סדורה)
גרף לא מכוון. סדרת קודקודים (סדורה) 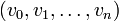 נקראת מסלול אם
נקראת מסלול אם
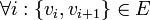 וגם כל הצלעות שונות - כלומר לכל
וגם כל הצלעות שונות - כלומר לכל 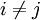 מתקיים כי
מתקיים כי 
מסלול יקרא פשוט אם כל הקודקודים 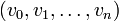 שונים זה מזה, פרט אולי ל
שונים זה מזה, פרט אולי ל 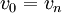
מעגל הוא מסלול פשוט המקיים 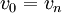
אורך המסלול 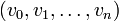 הוא
הוא 
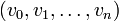 הינו מסלול מ
הינו מסלול מ 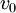 ל
ל 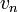
הגדרה
המרחק בין 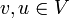 הוא המסלול עם אורך מינמאלי בין הקודקודים. (סימון
הוא המסלול עם אורך מינמאלי בין הקודקודים. (סימון 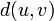 או
או 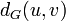 ).
).
אם אין מסלול בין 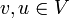 נסמן
נסמן 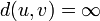
הקוטר של גרף  מוגדר כמרחק המקסימאלי בין 2 קודקודים . כלומר
מוגדר כמרחק המקסימאלי בין 2 קודקודים . כלומר 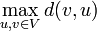
בניה
עבור גרף לא מכוון  נגדיר יחס שקילות
נגדיר יחס שקילות 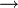 על
על  כך:
כך:
לכל 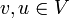 מתקיים
מתקיים 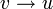 אמ"מ קיים מסלול מ
אמ"מ קיים מסלול מ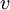 ל
ל 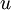 (כלומר
(כלומר 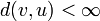 )
)
תרגיל: הוכח כי זהו יחס שקילות
הגדרה מחלקות השקילות של יחס זה נקראים רכיבי קשירות.
תרגילים
תרגיל: יהי גרף לא מכוון  בעל
בעל 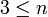 קודקודים.
אם בגרף
קודקודים.
אם בגרף 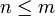 צלעות אזי בגרף יש מעגל.
צלעות אזי בגרף יש מעגל.
הוכחה: באינדוקציה.
עבור 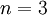 אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 קודקודים) ואכן מתקיים כי יש מעגל.
אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 קודקודים) ואכן מתקיים כי יש מעגל.
נניח כי הטכנה נכונה עבור  ונוכיח עבור
ונוכיח עבור 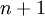 .
יהי יהי גרף לא מכוון
.
יהי יהי גרף לא מכוון  בעל
בעל 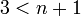 קודקודים ו-
קודקודים ו- 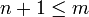 צלעות.
צלעות.
אפשרות 1: קיים 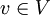 מדרגה 1. נוריד את הקודקוד הזה (ואת כל הצלעות שחלות בו) ונקבל גרף חדש עם
מדרגה 1. נוריד את הקודקוד הזה (ואת כל הצלעות שחלות בו) ונקבל גרף חדש עם  קודקודים ו
קודקודים ו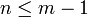 צלעות. לפי הנחת האינדוקציה קיים בו מעגל. מעגל זה קיים גם בגרף בו התחלנו.
צלעות. לפי הנחת האינדוקציה קיים בו מעגל. מעגל זה קיים גם בגרף בו התחלנו.
אפשרות 2: לכל קודקוד יש דרגה גדולה שווה 2. נבחר 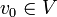 ונצא ממנו לאחד משכניו. מפה נמשיך למסלול רנדומאלי כך שאם הולכים מ
ונצא ממנו לאחד משכניו. מפה נמשיך למסלול רנדומאלי כך שאם הולכים מ 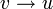 הצעד הבא לא יהיה
הצעד הבא לא יהיה 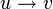 (זה אפשרי כי כל קודקוד יש לפחות 2 שכנים אז אם נכנסים אליו משכן א ניתן לצאת משכן ב). כיוון שיש מספר סופי של קודקודים נקבל חזרה על קודקוד בשלב כלשהוא. בפעם הראשונה שנקבל חזרה קיבלנו מעגל!
(זה אפשרי כי כל קודקוד יש לפחות 2 שכנים אז אם נכנסים אליו משכן א ניתן לצאת משכן ב). כיוון שיש מספר סופי של קודקודים נקבל חזרה על קודקוד בשלב כלשהוא. בפעם הראשונה שנקבל חזרה קיבלנו מעגל!
תרגיל:
יהי גרף לא מכוון  . הוכח כי אם
. הוכח כי אם 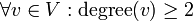 אז בגרף יש מעגל.
אז בגרף יש מעגל.
הוכחה: בגרף יש יותר מ 2 קודקודים (אחרת לא יהיה להם 2 שכנים).
לפי משפט לחיצת הידיים מתקיים 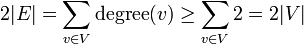 ולכן מספר הצלעות גדול שווה ממספר הקודקודים. לפי משפט קודם קיים מעגל בגרף.
ולכן מספר הצלעות גדול שווה ממספר הקודקודים. לפי משפט קודם קיים מעגל בגרף.
תרגיל:
יהי גרף לא מכוון  ללא מעגלים עם
ללא מעגלים עם 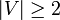 . הוכח כי קיימים
. הוכח כי קיימים 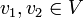 כך שדרגתם לכל היותר 1.
כך שדרגתם לכל היותר 1.
הוכחה: לפי תרגיל קודם קיים 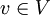 כך שדרגתו לכל היותר 1 (אחרת לכל הקודקודים יש דרגה לפחות 2 ואז יש מעגל לפי תרגיל קודם. סתירה!).
כך שדרגתו לכל היותר 1 (אחרת לכל הקודקודים יש דרגה לפחות 2 ואז יש מעגל לפי תרגיל קודם. סתירה!).
נמשיך באינדוקציה על  מספר הקודקודים בגרף.
מספר הקודקודים בגרף.
אם 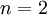 אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1.
אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1.
כעת נניח כי הטענה נכונה עבור 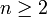 . נוכיח את הטענה עבור
. נוכיח את הטענה עבור 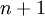 .
.
נבחר את הקודקוד 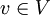 שדרגתו לכל היותר 1. נוריד אותו ואת הצלע שחלה בו אזי נקבל גרף עם
שדרגתו לכל היותר 1. נוריד אותו ואת הצלע שחלה בו אזי נקבל גרף עם  קודקודים. לפי הנחת האינדוקציה יש בו 2 קודקודים
קודקודים. לפי הנחת האינדוקציה יש בו 2 קודקודים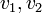 בעלי דרגה 1 לכל היותר. כעת נשוב לגרף המקורי (הכולל את
בעלי דרגה 1 לכל היותר. כעת נשוב לגרף המקורי (הכולל את 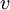 שהשמטנו).
שהשמטנו).
אם 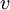 שכן של
שכן של 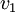 אזי
אזי 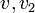 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
אם 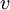 שכן של
שכן של 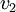 אזי
אזי 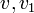 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
אם 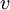 שכן של
שכן של 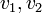 - סתירה כי הדרגה של
- סתירה כי הדרגה של 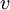 היא 1 לכל היותר.
היא 1 לכל היותר.
אם 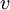 לא שכן של
לא שכן של 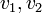 אזי
אזי 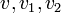 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
בכל מקרה קיבלנו כי קיימים 2 קודקודים בעלי דרגה 1 לכל היותר!.