הבדלים בין גרסאות בדף "לינארית 1 לתיכוניסטים תש"ע - שאלות ותשובות"
(←תרגיל 11.2) |
(←תשובה) |
||
| שורה 22: | שורה 22: | ||
===תשובה=== | ===תשובה=== | ||
הכוונה היא שb וx שניהם וקטורי עמודה (כלומר מגודל nx1 כפי שציינת) | הכוונה היא שb וx שניהם וקטורי עמודה (כלומר מגודל nx1 כפי שציינת) | ||
| + | :תודה! | ||
| + | :ועוד שאלה: כאשר נתון ש-<math>V</math> הוא מרחב העמודות של <math>A</math>, האם אני יכולה פשוט בלי להסביר כלום לכתוב ש: {<math>V=span{v_1,v_2,...,v_n}</math> כאשר <math>v_1,v_2,...v_n</math> הם וקטורי העמודות של <math>A</math>? | ||
| + | :דרך אגב, איך עושים סוגריים מסולסלים בתוך math? | ||
==בסיס== | ==בסיס== | ||
גרסה מ־01:04, 26 באוגוסט 2010
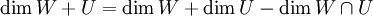
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)
ארכיון
ארכיון 1 - תרגיל 1
ארכיון 2 - תרגיל 2
ארכיון 3 - בוחן + תרגיל 3
ארכיון 4 - תרגיל 3
ארכיון 5 - תרגיל 4
שאלות
תרגיל 11.2
האם x הוא בהכרח וקטור מסדר n*1 או שהוא יכול להיות מטריצה?
תשובה
הכוונה היא שb וx שניהם וקטורי עמודה (כלומר מגודל nx1 כפי שציינת)
- תודה!
- ועוד שאלה: כאשר נתון ש-
הוא מרחב העמודות של 
, האם אני יכולה פשוט בלי להסביר כלום לכתוב ש: {
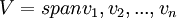כאשר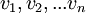 
הם וקטורי העמודות של ? - דרך אגב, איך עושים סוגריים מסולסלים בתוך math?
בסיס
הוצאתי חוברת לינארית מהספרייה, ובספר כתוב שכדי לוודא שוקטורים מסויימים a1,a2,...ak בת"ל, צריך לשים את הוקטורים כעמודות של מטריצה הומוגנית, ואז לצטט את שני המשפטים הבאים: במטריצה המורכבת מהעמודות a1,a2,...,ak,b (כך שכל עמודה היא וקטור), הוקטור b הוא צירוף לינארי של a1,...,ak כך שהמקדם של ai לכל i הוא xi אם"ם (x1,...xk) הוא פתרון של המערכת שלמעלה. בנוסף ידוע כי מטריצת מקדמים מצומצמת (כלומר מקדמים של מערכת משוואות לינאריות הומוגניות) היא שקולה למטריצת היחידה אם"ם אין למערכת פתרון לא טריוויאלי. כלומר נוכיח שהמטריצה שהרכבנו מהעמודות a1,...,ak,b שקולה למטריצת היחידה עפ"י פעולות שורה אלמנטריות, ולפי זה פתרון המערכת x1,...,xk הוא טריוויאלי כלומר 0=(x1,...,xk) ולכן ל- 0=x1a1+x2a2+...+xkak יש רק פתרון טריוויאלי לכן לפי הגדרה הווקטורים a1,...,ak בת"ל.
השאלה שלי היא האם מספיק לנמק: ידוע שאם מטריצה שקולה למטריצת היחידה אז כל עמודותיה בת"ל? נימוק כזה קצר יכול לחסוך המון זמן וכאב ראש...
תשובה
למדנו את התיאור הראשון בתרגיל - וגם השתמשנו בזה בפתרון תרגיל 3 (בקובץ המצורף). כמו כן למדנו שניתן לדרג את המטריצה ולראות האם שורות התאפסו לנו. אלה שתי שיטות שונות ושתיהן נכונות.
חשוב לשים לב ששקילות למטריצה היחידה היא רלוונטית רק כאשר מדובר על מטריצה ריבועית. וקטורים יכולים להיות בת"ל גם אם תשים אותם בעמודות מטריצה והיא תהיה לא ריבועית.
חשוב לזכור שכאשר אנו שמים וקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב הפתרונות. כאשר אנו שמים את הוקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב השורות.
11.10
המטריצות A B הן שתיהן מגודל MXN?ובהוכחה אני אמורה להניח שהשורות הן בת"ל ושהדרגה שווה למס' השורות? אם שתי המטריצות הן מגודל MXN אז מה הדרגה?
תשובה
לעולם לא מניחים דברים שלא כתובים בנתון. הגדלים של המטריצות נתונים - וזה נכון.
השורות לא חייבות להיות בת"ל בכלל.
שאלה לתשובה
תודה על התשובה אבל לא כ"כ עזרת לי, ברור לי שאי אפשר להניח משהו שהוא לא נתון, השאלה שלי היתה האם כדי להוכיח את מה שרצו אני מניחה שהם בת"ל,הרי במקרה כללי אני חייבת להניח את זה..לא?ובנוסף לא ענית לי מהי הדרגה של מטריצה(כללית, כלומר שלא יודעם את אבריה) MXN?מימד מרחב השורות/העמודות?
תשובה
זה כמו לשאול: האם x זוגי? התשובה המתבקשת כמובן היא תלוי מהו x.
אי אפשר להניח ששורות המטריצה בת"ל, הרי בוודאי יש מטריצות ששורותיהן תלויות לינארית. למה שתניחי דבר שהוא לא בהכרח נכון?
אין כזה דבר דרגה של מטריצת כללית. שוב, הדבר דומה לשאלה מהם הגורמים הראשוניים של מספר כללי x.
כאשר מנסים לפתור תרגיל כזה צריך לגשת אליו בצורה טכנית. לתת שמות לשורות המטריצות A,B ואז לראות מהן שורות המטריצה A+B, ואז לראות איך אפשר לחשב את הדרגה כפונקציה של השורות האלה וככה לנסות לפתור את התרגיל.
באופן כללי יש משפט לפיו דרגת המטריצה = מימד מרחב העמודות = מימד מרחב השורות = מספר המשתנים התלויים במערכת ההומוגנית = מספר השורות השונות מאפס בצורה המדורגת של המטריצה
תרגיל 2.8
מה הכוונה ב(א) שכתוב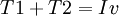 
? כלומר מה הכוונה בחיבור העתקות ליניאריות? תודה רבה... XD
תשובה
כמו שלמדנו בהרצאה ובתרגיל על המרחב הוקטורי של העתקות לינאריות -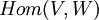 
:
יהיו 2 העתקות לינאריות T,S. נגדיר את ההעתקה הלינארית שהיא החיבור שלהן D=T+S, על ידי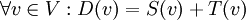 
תשובה לתשובה
תודה רבה XD :P :) :D
מרחב עמודות ***עוד שאלה***
איך מחשבים את הדרגה של A, כלומר את מספר האיברים בבסיס של מרחב העמודות של A? איך מוצאים את הבסיס? מהי הדרגה של מטריצת האפס? למה? תודה.
תשובה
- הדרגה של המטריצה היא מספר השורות השונות מאפס בצורה המדורגת שלה.
- אפשר למצוא בסיס למרחב העמודות על ידי:
- שחלוף המטריצה A
- דירוג המטריצה המשוחלפת
- שורות הצורה המדורגת של המטריצה המשוחלפת השונות מאפס, מהוות בסיס למרחב העמודות (כאשר מסתכלים עליהן כעמודות כמובן)
- מטריצה האפס היא בצורה מדורגת, אין שורות שונות מאפס ולכן הדרגה היא אפס.
- תודה, אבל נראה לי (לפי הגיון) שהדרגה של מטריצה היא מספר השורות שגם לא תלויות אחת בשניה (בת"ל), לא? נגיד המטריצה
1 2
2 4
הדרגה שלה היא 1 או 2? תודה.
- הדרגה היא אחד. המושג הכללי שאתה מאתר (מספר השורות שלא תלויות אחת בשנייה) מוגדר במדויק - הוא נקרא מימד. מימד הוא מספר האיברים בבסיס. ואם תביא את המטריצה הזו לצורה מדורגת תראה בקלות שיש רק שורה אחת שונה מאפס בצורה המדורגת, והיא מהווה בסיס למרחב השורות.
תרגיל 11.2ב
מהי המטריצה A|b?
- המטריצה A שהוסיפו לה מימין את העמודה b.
סכום ישר
לא הבנתי עד הסוף את הנושא של הסכום הישר! אתה יכול לתת דוגמא?
גם היתה דוג' בהרצאה שלא ממש הבנתי,
V=R^3 u=sp{(1,1,1)}, w={(x1,x2,x3)|x1+x2+x3=0, x1,x2,x3 in R טענה- v=u+w
צ"ל :
1. U+W מוכל בV.
2.V תת מרחב של U+W
3.U חיתוך W שווה 0.
למה צריך להוכיח את 2??
תשובה
הביטוי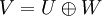 
אומר את שני הדברים הבאים לפי הגדרה:
א. V=U+W
ב.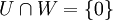 
על מנת להוכיח את א, צריך להוכיח את 1+2 שלך (זו סה"כ הכלה דו כיוונית שמוכיחה שיוויון).
ב' הוא בדיוק 3 שלך.
