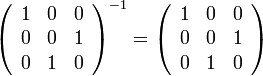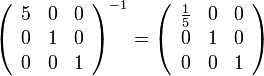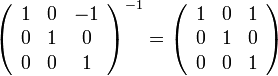הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/3"

גרסה מ־07:59, 9 ביולי 2015

תוכן עניינים

1 מטריצות הפיכות
- 1.1 תרגיל 6.1 וחצי
  - 1.1.1 פתרון
2 מציאת הופכית והצגה כמכפלה של מטריצות אלמנטריות
- 2.1 מטריצות אלמנטריות
- 2.2 מסקנה - אלגוריתם למציאת מטריצה הופכית

מטריצות הפיכות

הגדרה: מטריצה 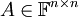$A\in \mathbb{F}^{n\times n}$ נקראת הפיכה אם קיימת מטריצה B כך ש 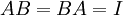$AB=BA=I$ . במקרה זה, מטריצה B נקראת ההופכית של A ומסומנת $B=A^{-1}$ .

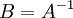הערות

מטריצה הפיכה היא בהכרח ריבועית
המטריצה ההופכית 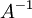$A^{-1}$ היא יחידה.

דוגמא:

ההופכית של המטריצה 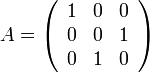$A=\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)$ היא $A$ עצמה.

נבדוק, אכן מתקיים ש 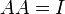$AA=I$ (קל לראות בעזרת כפל שורה-שורה)

משפט: אם A ריבועית ו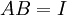 $AB=I$ אזי גם 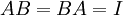$AB=BA=I$ וB הינה ההופכית של A. כלומר מטריצה שהפיכה מצד אחד הפיכה משני צדדים.

תרגיל: הוכח כי 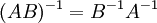$(AB)^{-1}=B^{-1}A^{-1}$

פתרון: מספיק להוכיח רק כי 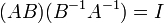$(AB)(B^{-1}A^{-1})=I$ (לפי משפט ממוקדם)

ואכן, בגלל קיבוציות כפל מטריצות + הגדרת הופכית, נקבל כי 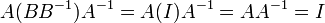$A(BB^{-1})A^{-1}=A(I)A^{-1}=AA^{-1}=I$

תרגיל (הכללה): יהיו עיבוד הנוסחה נכשל (שגיאת לקסינג): Aֹ_1,A_2,\dots A_k

מטריצות אזי

המכפלה 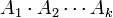$A_1\cdot A_2\cdots A_k$ הפיכה אמ"מ לכל 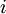$i$ מתקיים 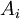$A_i$ הפיכה (כל המטריצות הפיכות). במקרה זה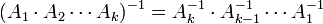 $(A_1\cdot A_2\cdots A_k)^{-1} = A_k^{-1} \cdot A_{k-1}^{-1}\cdots A_1^{-1}$

הוכחה (חלקית): כיוון ראשון (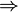 $\Rightarrow$ ) : בדיקה ישירה כי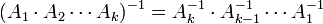 $(A_1\cdot A_2\cdots A_k)^{-1} = A_k^{-1} \cdot A_{k-1}^{-1}\cdots A_1^{-1}$

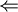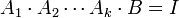כיוון שני ( $\Leftarrow$ ) : נתון שהמכפלה הפיכה. צריך להוכיח שכל אחת מהמטריצות הפיכה. נסמן את ההופכית של המכפלה ב $B$ אזי מתקיים לפי הגדרה כי $A_1\cdot A_2\cdots A_k\cdot B=I$ ומכאן רואים ישירות כי $A_1^{-1}=A_2\cdots A_k\cdot B$ .

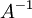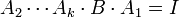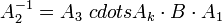כעת נכפיל ב $A^{-1}$ משמאל וב $A$ מימין ונקבל כי $A_2\cdots A_k\cdot B\cdot A_1=I$ ומכאן ש $A_2^{-1}= A_3\ cdots A_k\cdot B\cdot A_1$ וכן על זאת הדרך...

תרגיל 6.1 וחצי

הוכח שאם A הפיכה אזי גם המשוחלפת שלה הפיכה ומתקיים 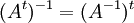$(A^t)^{-1}=(A^{-1})^t$ . הסק שאם A הפיכה וסמטרית אזי גם ההופכית שלה סימטרית.

פתרון

נניח A הפיכה, אזי קיימת לה הופכית כך ש 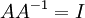$AA^{-1}=I$ . נשחלף את שני האגפים ונקבל 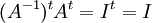$(A^{-1})^tA^t=I^t=I$ ומכאן המש"ל כיוון שA ריבועית וכך גם המשוחלפת שלה.

אם A הפיכה וסימטרית מתקיים 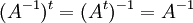$(A^{-1})^t=(A^t)^{-1}=A^{-1}$ כלומר ההופכית גם סימטרית.

מציאת הופכית והצגה כמכפלה של מטריצות אלמנטריות

דיברנו כבר על פעולות שורה אלמנטריות כאשר דיברנו על פעולות שלא משנות את מרחב הפתרונות של המערכת המתאימה למטריצה. נזכיר מהן פעולות השורה האלמנטריות:

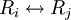
$R_i \leftrightarrow R_j$
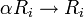$\alpha R_i \rightarrow R_i$ , כאשר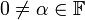 $0\neq\alpha\in\mathbb{F}$
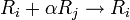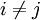
$R_i +\alpha R_j \rightarrow R_i$ כאשר $i\neq j$

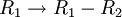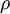את הפעולות הללו ביצענו על מטריצות (ככה דירגנו אותם). למשל נסמן את פעולת השורה $R_1\rightarrow R_1-R_2$ באות $\rho$ אזי מתקיים לדוגמא:

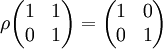
$\rho\begin{pmatrix}1 & 1 \\ 0 & 1\end{pmatrix}=\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$

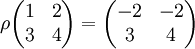
$\rho\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}=\begin{pmatrix}-2 & -2 \\ 3 & 4\end{pmatrix}$

כעת נרצה להחליף את ביצוע הפעולה בכפל במטריצה המכונה מטריצה אלמנטרית.

מטריצות אלמנטריות

מטריצת (שורה) אלמנטרית היא מטריצה המתקבלת מהפעלת פעולת שורה אלמנטרית על מטריצת היחידה.

דוגמאות (ב 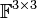$\mathbb{F}^{3\times3}$ ):

החלפת שורות 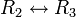$R_{2}\leftrightarrow R_{3}$ מתאים למטירצה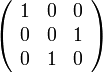 $\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)$
הכפלת שורה 1 ב-5 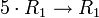$5\cdot R_{1}\rightarrow R_{1}$ מתאים למטריצה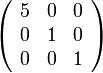 $\left(\begin{array}{ccc} 5 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)$
החסרת שורה 3 משורה 1 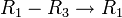$R_{1}-R_{3}\rightarrow R_{1}$ מתאים למטריצה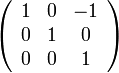 $\left(\begin{array}{ccc} 1 & 0 & -1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)$

משפט: לכל מטריצה A מתקיים 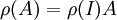$\rho(A) = \rho(I)A$ .

כלומר, הפעלת פעולת שורה אלמנטרית שקולה לכפל במטריצת השורה האלמנטרית המתאימה.

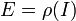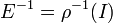משפט: מטריצה אלמנטרית $E=\rho(I)$ היא הפיכה ומתקיים $E^{-1}=\rho^{-1}(I)$ .

דוגמא: נמצא את ההופכית של המטריצות ממקודם:

$\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)^{-1}=\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)$
$\left(\begin{array}{ccc} 5 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)^{-1}=\left(\begin{array}{ccc} \frac{1}{5} & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)$
$\left(\begin{array}{ccc} 1 & 0 & -1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)^{-1}=\left(\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)$

יש משפט והגדרה דומים עבור מטריצות עמודה אלמנטריות עם כפל בצד השני. כמו כן, כל מטריצת שורה אלמנטרית הינה מטריצת עמודה אלמנטרית עבור פעולה מתאימה. מטריצות אלה נקראות ביחד מטריצות אלמנטריות.

מסקנה - אלגוריתם למציאת מטריצה הופכית

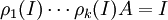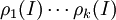דירוג מטריצה שקול לכפל במטריצות אלמנטריות המתאימות לפעולות הדירוג. לכן, אם דירגנו מטריצה ריבועית לצורת מטריצה היחידה קיבלנו $\rho_1(I)\cdots\rho_k(I)A=I$ ולפיכך מתקיים שהמטריצה A הפיכה וההופכית שלה הינה $\rho_1(I)\cdots\rho_k(I)$ .

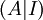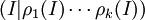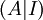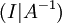אם נדרג קנונית את מטריצת הבלוקים $(A|I)$ נקבל מטריצה מהצורה $(I|\rho_1(I)\cdots\rho_k(I))$ (שכן לפי כפל מטריצת בלוקים, כפל במטריצה האלמנטרית מופעל במקביל על כל אחד מהבלוקים). לכן כאשר אנחנו מדרגים את $(A|I)$ עד שנקבל את מטריצת היחידה משמאל, מימין נקבל את המטריצה ההופכית $(I|A^{-1})$ .

@@ שורה 29: / שורה 29: @@
 ואכן, בגלל קיבוציות כפל מטריצות + הגדרת הופכית, נקבל כי <math>A(BB^{-1})A^{-1}=A(I)A^{-1}=AA^{-1}=I</math>
-תרגיל (הכללה): יהיו <math>Aֹ_1,A_2,\dots A_k</math> מטריצות אזי
+תרגיל (הכללה): יהיו <math>Aֹ_1,A_2,\dots A_k</math>
+מטריצות אזי
 המכפלה <math>A_1\cdot A_2\cdots A_k </math> הפיכה אמ"מ לכל <math>i</math> מתקיים <math>A_i</math> הפיכה (כל המטריצות הפיכות). במקרה זה <math>(A_1\cdot A_2\cdots A_k)^{-1} = A_k^{-1} \cdot A_{k-1}^{-1}\cdots A_1^{-1} </math>
 הוכחה (חלקית):
-כיוון ראשון (<math>\Leftarrow</math>) : בדיקה ישירה כי <math>(A_1\cdot A_2\cdots A_k)^{-1} = A_k^{-1} \cdot A_{k-1}^{-1}\cdots A_1^{-1} </math>
+כיוון ראשון  (<math>\Rightarrow</math>) : בדיקה ישירה כי <math>(A_1\cdot A_2\cdots A_k)^{-1} = A_k^{-1} \cdot A_{k-1}^{-1}\cdots A_1^{-1} </math>
-כיוון שני (<math>\Rightarrow</math>) : נתון שהמכפלה הפיכה. צריך להוכיח שכל אחת מהמטריצות הפיכה. נסמן את ההופכית של המכפלה ב <math>B</math> אזי מתקיים לפי הגדרה כי <math>A_1\cdot A_2\cdots A_k\cdot B=I </math> ומכאן רואים ישירות כי <math>A_1^{-1}=A_2\cdots A_k\cdot B </math>.
+כיוון שני (<math>\Leftarrow</math>) : נתון שהמכפלה הפיכה. צריך להוכיח שכל אחת מהמטריצות הפיכה. נסמן את ההופכית של המכפלה ב <math>B</math> אזי מתקיים לפי הגדרה כי <math>A_1\cdot A_2\cdots A_k\cdot B=I </math> ומכאן רואים ישירות כי <math>A_1^{-1}=A_2\cdots A_k\cdot B </math>.
 כעת נכפיל ב <math>A^{-1}</math> משמאל וב <math>A</math> מימין ונקבל כי <math> A_2\cdots A_k\cdot B\cdot A_1=I </math>

הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/3"

גרסה מ־07:59, 9 ביולי 2015

תוכן עניינים

מטריצות הפיכות

תרגיל 6.1 וחצי

פתרון

מציאת הופכית והצגה כמכפלה של מטריצות אלמנטריות

מטריצות אלמנטריות

מסקנה - אלגוריתם למציאת מטריצה הופכית

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים