הבדלים בין גרסאות בדף "אסימפטוטה משופעת"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) מ |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 3: | שורה 3: | ||
==הגדרה== | ==הגדרה== | ||
אומרים כי לפונקציה ממשית <math>f</math> קיימת אסימפטוטה משופעת באינסוף אם קיימים קבועים <math>a,b</math> כך ש: | אומרים כי לפונקציה ממשית <math>f</math> קיימת אסימפטוטה משופעת באינסוף אם קיימים קבועים <math>a,b</math> כך ש: | ||
| − | + | :<math>\lim\limits_{x\to\infty}\big[f(x)-ax-b\big]=0</math> | |
במקרה זה האסימפטוטה המשופעת באינסוף הנה <math>y=ax+b</math> . | במקרה זה האסימפטוטה המשופעת באינסוף הנה <math>y=ax+b</math> . | ||
באופן דומה, לפונקציה <math>f</math> קיימת אסימפטוטה משופעת במינוס אינסוף אם קיימים קבועים <math>a,b</math> כך ש: | באופן דומה, לפונקציה <math>f</math> קיימת אסימפטוטה משופעת במינוס אינסוף אם קיימים קבועים <math>a,b</math> כך ש: | ||
| − | :<math>\ | + | :<math>\lim\limits_{x\to-\infty}\big[f(x)-ax-b\big]=0</math> |
==מציאת אסימפטוטה משופעת== | ==מציאת אסימפטוטה משופעת== | ||
| − | נניח וקיימת אסימפוטטה משופעת, אזי | + | נניח וקיימת אסימפוטטה משופעת, אזי |
| − | :<math>\ | + | :<math>\lim\limits_{x\to\infty}\big[f(x)-ax-b\big]=0</math> |
לכן | לכן | ||
| − | :<math>\ | + | :<math>\lim\limits_{x\to\infty}\left[\dfrac{f(x)-ax-b}{x}\right]=0</math> |
ולכן | ולכן | ||
| − | :<math>\ | + | :<math>\lim\limits_{x\to\infty}\dfrac{f(x)}{x}=a</math> |
כלומר: | כלומר: | ||
| − | *'''שלב ראשון:''' שיפוע האסימפטוטה המשופעת הנו <math>a=\ | + | *'''שלב ראשון:''' שיפוע האסימפטוטה המשופעת הנו <math>a=\lim\limits_{x\to\infty}\dfrac{f(x)}{x}</math> . אם הגבול אינו קיים אין אסימפטוטה משופעת. |
| − | *'''שלב שני:''' חיתוך האסימפטוטה עם ציר <math>y</math> הנו <math>b=\ | + | *'''שלב שני:''' חיתוך האסימפטוטה עם ציר <math>y</math> הנו <math>b=\lim\limits_{x\to\infty}\big[f(x)-ax\big]</math> . אם הגבול אינו קיים אין אסימפטוטה משופעת. |
עבור <math>-\infty</math> התהליך דומה. | עבור <math>-\infty</math> התהליך דומה. | ||
גרסה אחרונה מ־06:27, 14 בפברואר 2017
פונקציה בעלת אסימפטוטה משופעת הנה פונקציה ששואפת להיות קו ישר באינסוף. פונקציה בעלת גבול סופי באינסוף שואפת לקו ישר מאוזן, אך ישנן פונקציה השואפות לקו ישר משופע.
הגדרה
אומרים כי לפונקציה ממשית  קיימת אסימפטוטה משופעת באינסוף אם קיימים קבועים
קיימת אסימפטוטה משופעת באינסוף אם קיימים קבועים 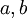 כך ש:
כך ש:
במקרה זה האסימפטוטה המשופעת באינסוף הנה 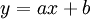 .
.
באופן דומה, לפונקציה  קיימת אסימפטוטה משופעת במינוס אינסוף אם קיימים קבועים
קיימת אסימפטוטה משופעת במינוס אינסוף אם קיימים קבועים 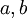 כך ש:
כך ש:
מציאת אסימפטוטה משופעת
נניח וקיימת אסימפוטטה משופעת, אזי
לכן
ולכן
כלומר:
- שלב ראשון: שיפוע האסימפטוטה המשופעת הנו
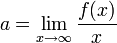 . אם הגבול אינו קיים אין אסימפטוטה משופעת.
. אם הגבול אינו קיים אין אסימפטוטה משופעת. - שלב שני: חיתוך האסימפטוטה עם ציר
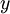 הנו
הנו ![b=\lim\limits_{x\to\infty}\big[f(x)-ax\big]](/images/math/e/3/a/e3afbef07df28812ce2b3deac4eb992b.png) . אם הגבול אינו קיים אין אסימפטוטה משופעת.
. אם הגבול אינו קיים אין אסימפטוטה משופעת.
עבור 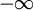 התהליך דומה.
התהליך דומה.
![\lim\limits_{x\to\infty}\big[f(x)-ax-b\big]=0](/images/math/8/4/6/8463b1681e5d7c7a13ca65c8f71087a8.png)
![\lim\limits_{x\to-\infty}\big[f(x)-ax-b\big]=0](/images/math/3/4/f/34f7dcccdb0485134ab6e70122b5e62b.png)
![\lim\limits_{x\to\infty}\left[\dfrac{f(x)-ax-b}{x}\right]=0](/images/math/d/c/7/dc7e1db4d9ceffbf7c8a82baf497ee9b.png)