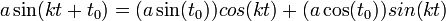הבדלים בין גרסאות בדף "אנליזת פורייה - ארז שיינר"
מתוך Math-Wiki
(←גלים) |
(←גלים) |
||
| שורה 33: | שורה 33: | ||
**לגל החדש יש פאזה שאינה אפס. | **לגל החדש יש פאזה שאינה אפס. | ||
**האפליטודה של הגל החדש היא <math>r=\sqrt{a^2+b^2}</math>. | **האפליטודה של הגל החדש היא <math>r=\sqrt{a^2+b^2}</math>. | ||
| + | |||
| + | |||
| + | *האם כל פונקציה היא סכום של גלים? | ||
| + | *בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה? | ||
| + | *האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים). | ||
| + | *למה בכלל מעניין אותנו לפרק פונקציה לגלים? | ||
| + | *במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו. | ||
==טורי פורייה== | ==טורי פורייה== | ||
גרסה מ־08:09, 19 בפברואר 2019
תוכן עניינים
מבחנים לדוגמא
תקציר ההרצאות
הקדמה
גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה
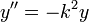 שהפתרון הכללי שלה הוא
שהפתרון הכללי שלה הוא 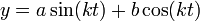 .
. - הקבוע
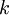 קובע את התדר של כל גל.
קובע את התדר של כל גל. - הקבועים
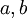 קובעים את האמפליטודה של כל גל.
קובעים את האמפליטודה של כל גל. - מה לגבי הפאזה?
- בפונקציה
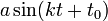 , הקבוע
, הקבוע 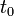 קובע את הפאזה.
קובע את הפאזה. - ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- בפונקציה
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי
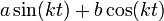 ניתן להציג כגל יחיד?
ניתן להציג כגל יחיד? - תשובה: כן.
- הוכחה:
- נסמן
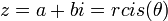
- כלומר
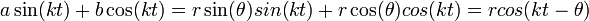
- נסמן
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא
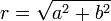 .
.
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.