גרסה מ־17:15, 7 בדצמבר 2010

חזרה לדף הקורס

גלול לתחתית העמוד

תוכן עניינים

1 הוספת שאלה חדשה
2 ארכיון
3 שאלות

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

שאלות

כמה שאלות עם החומר שנלמד לאחרונה

שלום, החומר שנלמד לאחרונה, על מכפלה פנימית, בסיסים אורתונורמליים וכדומה לא יושב אצלי טוב. גיליתי שמאוד עוזר אם מבינים מה המקבילים של המושגים שלמדנו במרחב (כמו ניצבות, מכפלה פנימית=מכפלה סקלרית וכו'). אך לכמה לא מצאתי מקבילים ולכן קשה לי להבין בדיוק מה הם אומרים או למה הם משמשים. דבר ראשון, האם יש מקביל לבסיס אורתוגונלי או אורתונורמלי במרחב, ואם כן למה צריך אותו? ודבר שני, למה, או האם יש מקביל במרחב, לכך שההיטל של וקטור (על תת מרחב, ביחס לבסיס אורתונורמלי B={w1,..,wk} ) הוא 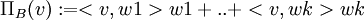$\Pi _B(v):=<v,w1>w1+..+<v,wk>wk$ ? תודה!

אני לא בטוחה למה אתה מתכוון מקביל במרחב אבל בסיס אורתוגונלי במרחב יושב על הצירים או על כל הזזה שלהם בו ללא הזזה שלהם אחד ביחס לשני. "צריך" אורתוג' כי יותר נוח לעבוד איתו מבחינה של זוית ואורתונ' כי יותר נוח לעבוד איתו מבחינה של אורך (בשניהם "יותר נוח" הכוונה במכפלה הפנימית). לגבי החלק השני : כי אתה יוצר צרוף לנארי שלו מההטלה שלו לכל תת מרחב שכל וקטור בסיס יוצר. ראה אילוסטרציה מאת דר' צבאן בעמוד הראשי.

עוד שאלה

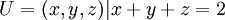תודה רבה, אבל לא הבנתי את התשובה לחלק השני, אשמח להסבר. וגם יש לי עוד שאלה: במרחב (R^3), ישר ומישור הם תתי מרחבים? אם כן, איך מציגים אותם בצורת תת מרחב? (כלומר למישור בצורה $U={u\in U| u...}$ ? אפשר ככה $U={(x,y,z)|x+y+z=2}$ לדוגמה? ואיך לישר?) אם כן, אז המרחב הניצב לישר/מישור הוא ישר, מישור, או משהו אחר? תודה!!

תרגיל האתגר

במידה ונצליח לפתור את תרגיל האתגר, מה בדיוק צריך לעשות עם הפתרון? האם לשלוח אותו למרצה? ואם כן אז איך בדיוק? -לידור.א.- 21:43, 4 בדצמבר 2010 (IST)

אתה יכול לשלוח אימייל לד"ר צבאן, הכתובת רשומה באתר שלו http://u.cs.biu.ac.il/~tsaban/ . דורון פרלמן 22:20, 4 בדצמבר 2010 (IST)

האם צריך להוכיח

לגבי שתי הטענות הבאות: -לכל מרחב ממימד סופי יש בסיס; -כל בסיס אפשר להפוך לבסיס א"נ ע"י תהליך גראם שמידט- האם ניתן להגיד "כפי שעשינו בהרצאה" או "על פי משפט" וכו', או שצריך להוכיח אותן (מחדש)? תודה!

איפה? אם זה חלק מהוכחה כללית יותר ניתן להשתמש,אם זה מהות כל השאלה (כמו בדף 8, 4.16א) אז צריך להוכיח.

גם את העובדה שלכל מרחב סופי יש בסיס?? זה ממש מסובך, כשחיפשתי את זה מצאתי שכדי להוכיח את זה צריך להסתמך על הלמה של צורן..

אני חוזרת לאותה תשובה: איפה?

בשאלה 4.16

אתה יכול להשתמש בקיום בסיס ללא הוכחה

שאלה קטנה (שנתקלתי בה בזמן הוכחה תהליך ג"ש)

האם אני תמיד יכול להגיד ש 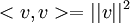$<v,v>=||v||^2$ ? זה נכון ממהגדרה כשהנורמה היא נורמה שמושרית מהמ"פ, אבל יכול להיות שכשהנורמה לא מושרית אז זה לא נכון? (אני חייב שזה יהיה נכון כדי להוכיח את נכונות תהליך ג"ש)...

לעניות דעתי בתהליך גראם-שמידט מדובר בנורמה המושרית -לידור.א.- 23:25, 5 בדצמבר 2010 (IST)

עוד שאלה קטנה, על מ"פ

אם ידוע ש 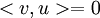$<v,u>=0$ , ו-u שונה מוקטור האפס, אזי בטוח v שווה לוקטור האפס או לא בהכרח? תודה!

בטח שלא, המכפלה הפנימית של כל שני וקטורים מאונכים היא אפס.

אה נכון התבלבלתי לגמרי. תודה

עבודת ההגשה

בעבודת ההגשה תרגיל 1 סעיף ב' מה זה lcm ?

קרא כאן:

כפולה משותפת מינימלית

(אופיר ר.)

מימד של חיתוך/איחוד

האם ידועים המימדים של חיתוך ו/או איחוד של תתי מרחבים (כלומר האם המימד של חיתוך של 2 תתי מרחבים שווה למינימלי מבין המימדים של 2 המרחבים, או פונקציה כלשהי אחרת של 2 המימדים של 2 תתי המרחבים וכנ"ל באיחוד)? תודה!

תשובה

לגבי איחוד - לא כל איחוד של שני תתי מרחבים ייתן תת מרחב, לגבי מה יהיה המימד במידה ונקבל תת מרחב - אינני יודע. לגבי חיתוך - בוודאי שזה לא המינימלי - דוגמה נגדית: $V=Sp(1,0)\ \ \ U=Sp(0,1)$ . המימד של כל אחד מהם הוא אחד, אבל החיתוך ביניהם הוא מרחב האפס ומימדו הוא אפס.

מקווה שהצלחתי לעזור, גל א.

שאלה על האתגר

מה אומר ה-ker של T-kI בחזקת n? זה העתקה בחזקת n (אם כן, הכוונה היא להעתקה T-ki אן פעמים?) או ker בחזקת n (ואז הכוונה היא n-יה סדורה של איברים מהker?) תודה!

מדובר בגרעין של ההעתקה

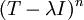(T - \lambda I)^n

, כלומר מרחב הפתרונות של

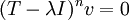{(T - \lambda I)^n}v = 0

-לידור.א.- 16:22, 6 בדצמבר 2010 (IST)

העתקה צמודה

האם ההעתקה הצמודה היא בחומר, ואם כן אז מהי? תודה! לא. זה הנושא הבא

מכפלה פנימית

האם אפשר להגדיר על כל מרחב וקטורי ממימד סופי מכפלה פנימית? ואם כן צריך להוכיח את זה?

שאלה ממבחן (דחוף לבוחן)

שלום, במבחן 2003 מועד א' (http://u.cs.biu.ac.il/~tsaban/Pdf/lin2a63.pdf), חלק אמריקאי שאלה 4, על מכפלות פנימיות- בתשובות כתבו שהתשובה הנכונה היא 1, שתי ה'מ"פ' הנתונות הן לא מ"פ. 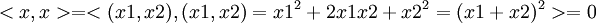אבל לדעתי התשובה הנכונה היא 4, שA היא מ"פ וB לא- כי שתי הפונקציות מקיימות לינארית ברכיב הראשון, הפונקציה B לא מקיימת סימטריה (מעל R ולא C) ולא אי שליליות, אבל A כן מקיימת את הכל, כי היא גם סימטרית, בקלות לפי חילופיות הכפל, והיא אי שלילית, מכיוון ש $<x,x>=<(x1,x2),(x1,x2)=x1^2+2x1x2+x2^2=(x1+x2)^2>=0$ (ו0 כשx=0 כמובן). איפה אני טועה? תודה!

@@ שורה 93: / שורה 93: @@
 שלום,
 במבחן 2003 מועד א' (http://u.cs.biu.ac.il/~tsaban/Pdf/lin2a63.pdf), חלק אמריקאי שאלה 4, על מכפלות פנימיות- בתשובות כתבו שהתשובה הנכונה היא 1, שתי ה'מ"פ' הנתונות הן לא מ"פ. אבל לדעתי התשובה הנכונה היא 4, שA היא מ"פ וB לא- כי שתי הפונקציות מקיימות לינארית ברכיב הראשון, הפונקציה B לא מקיימת סימטריה (מעל R ולא C) ולא אי שליליות, אבל A כן מקיימת את הכל, כי היא גם סימטרית, בקלות לפי חילופיות הכפל, והיא אי שלילית, מכיוון ש
-<math><x,x>=<(x1,x2),(x1,x2)=x1^2+x1x2+x2^2=(x1+x2)^2>=0</math> (ו0 כשx=0 כמובן). איפה אני טועה? תודה!
+<math><x,x>=<(x1,x2),(x1,x2)=x1^2+2x1x2+x2^2=(x1+x2)^2>=0</math> (ו0 כשx=0 כמובן). איפה אני טועה? תודה!

הבדלים בין גרסאות בדף "שיחה:88-113 סמסטר א' תשעא/קבוצת דיון-עדי ניב"

גרסה מ־17:15, 7 בדצמבר 2010

תוכן עניינים

הוספת שאלה חדשה

ארכיון

שאלות

כמה שאלות עם החומר שנלמד לאחרונה

עוד שאלה

תרגיל האתגר

האם צריך להוכיח

שאלה קטנה (שנתקלתי בה בזמן הוכחה תהליך ג"ש)

עוד שאלה קטנה, על מ"פ

עבודת ההגשה

מימד של חיתוך/איחוד

תשובה

שאלה על האתגר

העתקה צמודה

מכפלה פנימית

שאלה ממבחן (דחוף לבוחן)

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים