גרסה מ־11:19, 2 במאי 2011

תוכן עניינים

1 מבוא לאינטגרציה נומרית (המשך)
- 1.1 דוגמה
2 אינטגרל לא אמיתי, סוג I
- 2.1 דוגמאות

מבוא לאינטגרציה נומרית (המשך)

בהרצאה הקודמת הצגנו את כלל סימפסון לקירוב האינטגרל המסויים והראנו שהטעות בחישוב בקטע $[a,b]$ חסומה ע"י $\max_{x\in[a,b]}\left|f^{(4)}(x)\right|\frac{h^4(b-a)}{45}$ כאשר h המרחק בין שתי נקודות סמוכות בחלוקה שבחרנו. ניתן גישה אחרת למציאת הטעות, שהיא יותר קצרה ונותנת ערך יותר קטן לחסם של הטעות, אבל היא פחות אינטואיטיבית:

ע"י נירמול מספיק לחשב בקירוב

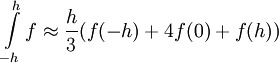\int\limits_{-h}^h f\approx\frac h3(f(-h)+4f(0)+f(h))

כאשר f גזירה 4 פעמים בסביבת 0. נגדיר פונקציה חדשה

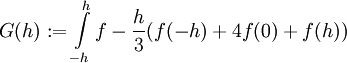G(h):=\int\limits_{-h}^h f-\frac h3(f(-h)+4f(0)+f(h))

. G מוגדרת ורציפה בסביבה של 0 וגם (לפי הצבה)

G(0)=0

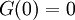. עבור F קדומה ל-f מתקיים (לפי המשפט היסודי)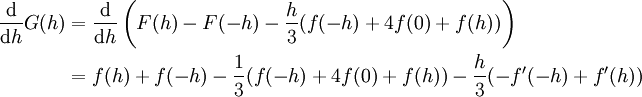

\begin{align}\frac\mathrm d{\mathrm dh}G(h)&=\frac\mathrm d{\mathrm dh}\left(F(h)-F(-h)-\frac h3(f(-h)+4f(0)+f(h))\right)\\&=f(h)+f(-h)-\frac13(f(-h)+4f(0)+f(h))-\frac h3(-f'(-h)+f'(h))\end{align}

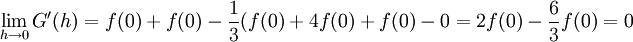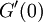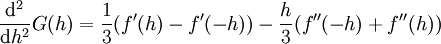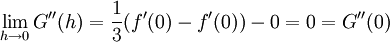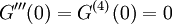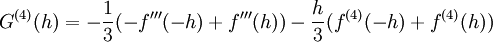לכן $\lim_{h\to0}G'(h)=f(0)+f(0)-\frac13(f(0)+4f(0)+f(0)-0=2f(0)-\frac63f(0)=0$ . ע"פ הלמה השנייה בהרצאה הקודמת $G'(0)$ קיים ושווה ל-0. נגזור שוב את G ונקבל $\frac{\mathrm d^2}{\mathrm dh^2}G(h)=\frac13(f'(h)-f'(-h))-\frac h3(f''(-h)+f''(h))$ . מכאן ש- $\lim_{h\to0}G''(h)=\frac13(f'(0)-f'(0))-0=0=G''(0)$ . נמשיך לגזור פעמיים נוספות ונקבל $G'''(0)=G^{(4)}(0)=0$ וגם $G^{(4)}(h)=-\frac13(-f'''(-h)+f'''(h))-\frac h3(f^{(4)}(-h)+f^{(4)}(h))$ . עתה:

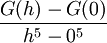
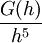
	$\frac{G(h)-G(0)}{h^5-0^5}$	$=$	$\frac{G(h)}{h^5}$
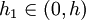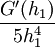
לפי משפט קושי קיים $h_1\in(0,h)$ עבורו:	$\frac{G'(h_1)}{5h_1^4}$	$=$
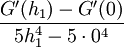
	$\frac{G'(h_1)-G'(0)}{5h_1^4-5\cdot0^4}$	$=$
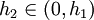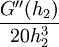
קיים $h_2\in(0,h_1)$ עבורו:	$\frac{G''(h_2)}{20h_2^3}$	$=$
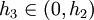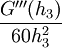
קיים $h_3\in(0,h_2)$ עבורו:	$\frac{G'''(h_3)}{60h_3^2}$	$=$
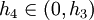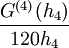
קיים $h_4\in(0,h_3)$ עבורו:	$\frac{G^{(4)}(h_4)}{120h_4}$	$=$

כעת נגדיר

M:=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|

. לפי משפט לגראנז' קיים

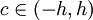c\in(-h,h)

כך ש-

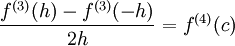\frac{f^{(3)}(h)-f^{(3)}(-h)}{2h}=f^{(4)}(c)

ולכן

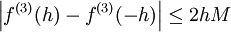\left|f^{(3)}(h)-f^{(3)}(-h)\right|\le2hM

. מכל זה נובע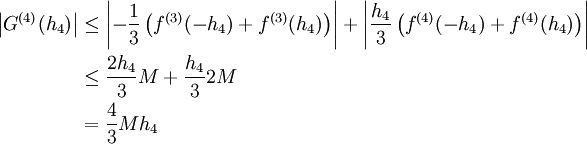

\begin{align}\left|G^{(4)}(h_4)\right|&\le\left|-\frac13\left(f^{(3)}(-h_4)+f^{(3)}(h_4)\right)\right|+\left|\frac{h_4}3\left(f^{(4)}(-h_4)+f^{(4)}(h_4)\right)\right|\\&\le\frac{2h_4}3M+\frac{h_4}32M\\&=\frac43Mh_4\end{align}

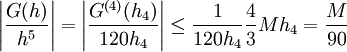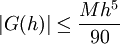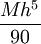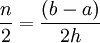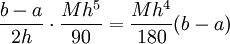עתה $\left|\frac{G(h)}{h^5}\right|=\left|\frac{G^{(4)}(h_4)}{120h_4}\right|\le\frac1{120h_4}\frac43Mh_4=\frac M{90}$ וקיבלנו ש- $|G(h)|\le\frac{Mh^5}{90}$ , כלומר הטעות בכל קטע מהסוג $[x_{k-1},x_{k+1}]$ חסומה ע"י $\frac{Mh^5}{90}$ . ב- $[a,b]$ יש $\frac n2=\frac{(b-a)}{2h}$ ולפיכך הטעות חסומה ע"י $\frac{b-a}{2h}\cdot\frac{Mh^5}{90}=\frac{Mh^4}{180}(b-a)$ . $\blacksquare$

דוגמה

נקרב 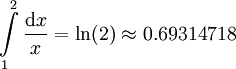$\int\limits_1^2\frac{\mathrm dx}x=\ln(2)\approx0.69314718$ . נבחר 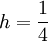$h=\frac14$ . נציב:

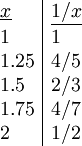
\begin{array}{l|l}\underline x&\underline{1/x}\\1&1\\1.25&4/5\\1.5&2/3\\1.75&4/7\\2&1/2\end{array}

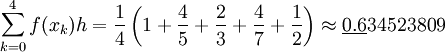הקירוב לפי סכום רימן הוא $\sum_{k=0}^4f(x_k)h=\frac14\left(1+\frac45+\frac23+\frac47+\frac12\right)\approx\underline{0.6}34523809$ .
כעת נעשה קירוב בשיטת הטרפזים:
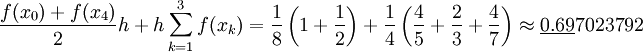
$\frac{f(x_0)+f(x_4)}2h+h\sum_{k=1}^3f(x_k)=\frac18\left(1+\frac12\right)+\frac14\left(\frac45+\frac23+\frac47\right)\approx\underline{0.69}7023792$
ולפי סימפסון:
$\begin{array}{l}\frac h3\left(f(x_0)+4\sum_{k=1}^{2}f(x_{2k-1})+2\sum_{k=1}^{1}f(x_{2k})+f(x_4)\right)\\=\frac1{12}\left(1+4\frac45+2\frac23+4\frac47+\frac12\right)\\\approx\underline{0.693}253968\end{array}$
נחשב את סדר הגודל של הטעות בקירוב סימפסון:
$f'(x)=-x^{-2}\implies f''(x)=2x^{-3}\implies f^{(3)}(x)=-6x^{-4}\implies f^{(4)}(x)=24x^{-5}$
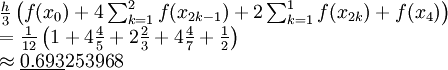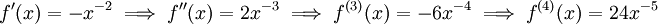
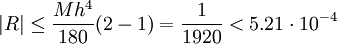
ולכן $M=\max_{x\in[1,2]}\left|24x^{-5}\right|=24$ והטעות R בקירוב מקיימת $|R|\le\frac{Mh^4}{180}(2-1)=\frac1{1920}<5.21\cdot10^{-4}$

אינטגרל לא אמיתי, סוג I

עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי" (improper integral).

אינטגרלים של קטעים אינסופיים מהסוג 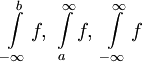$\int\limits_{-\infty}^b f,\ \int\limits_a^\infty f,\ \int\limits_{-\infty}^\infty f$ .

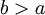הגדרה: תהי f פונקציה מוגדרת בקטע מהסוג $[a,\infty)$ . נאמר ש-f אינטגרבילית מקומית (locally integrable) בקטע זה אם לכל $b>a$ f אינטגרבילית בקטע $[a,b]$ .

למשל, אם f רציפה למקוטעין אז היא אינטגרבילית מקומית.

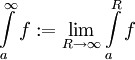הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב- $[a,\infty)$ נגדיר $\int\limits_a^\infty f:=\lim_{R\to\infty}\int\limits_a^R f$ . אם הגבול קיים נאמר שהאינטגרל מתכנס, אחרת הוא מתבדר.

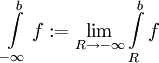אינטגביליות מקומית מוגדרת באופן דומה עבור קטע מהצורה $(-\infty,b]$ ואם f אינטגרבילית מקומית שם נגדיר $\int\limits_{-\infty}^b f:=\lim_{R\to-\infty}\int\limits_R^b f$ .

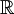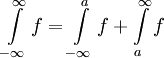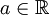עבור f מוגדרת בכל $\mathbb R$ נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית מקומית בכל קטע סופי, ואם כן נגדיר $\int\limits_{-\infty}^\infty f=\int\limits_{-\infty}^a f+\int\limits_a^\infty f$ עבור $a\in\mathbb R$ כרצוננו עבורו שני האינטגרלים באגף ימין מתכנסים.

דוגמאות

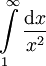$\int\limits_1^\infty\frac{\mathrm dx}{x^2}$ . נחשב:
$\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R\frac{\mathrm dx}{x^2}\\&=\lim_{R\to\infty}\left[-\frac1x\right]_{x=1}^R\\&=\lim_{R\to\infty}\left(-\frac1R+1\right)\\&=1\end{align}$
ניתן גם לכתוב בקיצור: $\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\left[-\frac1x\right]_{x=1}^\infty=0-(-1)=1$ .
$\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\ln(\infty)-0=\infty$ , כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב).
שאלה מארה"ב מלפני הרבה שנים: חצוצרה אינסופית תתקבל מסיבוב הגרף 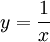$y=\frac1x$ סביב ציר ה-x ב- 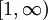$[1,\infty)$ . איך צובעים אותו מבפנים?
פתרון: לכאורה זה בלתי אפשרי, כי שטח הפנים של החצוצרה הוא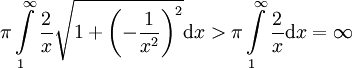 $\pi\int\limits_1^\infty\frac2x\sqrt{1+\left(-\frac1{x^2}\right)^2}\mathrm dx>\pi\int\limits_1^\infty\frac2x\mathrm dx=\infty$ , כלומר אין מספיק צבע בעולם. אך מכיוון שכמות הצבע נמדדת ביחידות נפח ולא שטח, ומכיוון שהנפח בתוך החצוצרה הוא 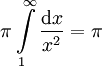$\pi\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\pi$ , יספיקו לנו 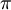$\pi$ יחידות מעוקבות של צבע ואפילו ישאר לנו עודף.

שאלה: האם התכנסות האינטגרל 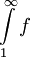$\int\limits_1^\infty f$ גוררת ש- 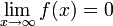$\lim_{x\to\infty} f(x)=0$ (בדומה לטורים)?

תשובה: לא. נגדיר פונקציה f שהגרף שלה הוא

אזי

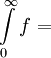\int\limits_0^\infty f=

השטח שמתחת לגרף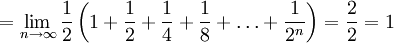

=\lim_{n\to\infty}\frac12\left(1+\frac12+\frac14+\frac18+\dots+\frac1{2^n}\right)=\frac22=1

כלומר האינטגרל מתכנס, אבל 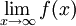$\lim_{x\to\infty} f(x)$ לא קיים.

@@ שורה 32: / שורה 32: @@
 * ולפי סימפסון: {{left|<math>\begin{array}{l}\frac h3\left(f(x_0)+4\sum_{k=1}^{2}f(x_{2k-1})+2\sum_{k=1}^{1}f(x_{2k})+f(x_4)\right)\\=\frac1{12}\left(1+4\frac45+2\frac23+4\frac47+\frac12\right)\\\approx\underline{0.693}253968\end{array}</math>}} נחשב את סדר הגודל של הטעות בקירוב סימפסון: {{left|<math>f'(x)=-x^{-2}\implies f''(x)=2x^{-3}\implies f^{(3)}(x)=-6x^{-4}\implies f^{(4)}(x)=24x^{-5}</math>}} ולכן <math>M=\max_{x\in[1,2]}\left|24x^{-5}\right|=24</math> והטעות R בקירוב מקיימת <math>|R|\le\frac{Mh^4}{180}(2-1)=\frac1{1920}<5.21\cdot10^{-4}</math>
-=אינטגרל לא אמיתי {{הערה|(improper integral)}}=
+=אינטגרל לא אמיתי, סוג I=
-עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי".
+עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי" (improper integral).
-==סוג א==
 אינטגרלים של קטעים אינסופיים מהסוג <math>\int\limits_{-\infty}^b f,\ \int\limits_a^\infty f,\ \int\limits_{-\infty}^\infty f</math>.
@@ שורה 47: / שורה 47: @@
 עבור f מוגדרת בכל <math>\mathbb R</math> נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית מקומית בכל קטע סופי, ואם כן נגדיר <math>\int\limits_{-\infty}^\infty f=\int\limits_{-\infty}^a f+\int\limits_a^\infty f</math> עבור <math>a\in\mathbb R</math> כרצוננו עבורו שני האינטגרלים באגף ימין מתכנסים.
-===דוגמאות===
+==דוגמאות==
 # <math>\int\limits_1^\infty\frac{\mathrm dx}{x^2}</math>. נחשב: {{left|<math>\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R\frac{\mathrm dx}{x^2}\\&=\lim_{R\to\infty}\left[-\frac1x\right]_{x=1}^R\\&=\lim_{R\to\infty}\left(-\frac1R+1\right)\\&=1\end{align}</math>}} ניתן גם לכתוב בקיצור: <math>\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\left[-\frac1x\right]_{x=1}^\infty=0-(-1)=1</math>.
 # <math>\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\ln(\infty)-0=\infty</math>, כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב).

הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/3.4.11"

גרסה מ־11:19, 2 במאי 2011

תוכן עניינים

מבוא לאינטגרציה נומרית (המשך)

דוגמה

אינטגרל לא אמיתי, סוג I

דוגמאות

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים