הבדלים בין גרסאות בדף "שיחה:88-112 לינארית 1 תיכוניסטים קיץ תשעא"
(←6.20 ??????) |
|||
| שורה 1: | שורה 1: | ||
{{הוראות דף שיחה}} | {{הוראות דף שיחה}} | ||
| + | |||
| + | =ארכיון= | ||
| + | [[88-112 לינארית 1 תיכוניסטים קיץ תשעא/ארכיון 1|ארכיון 1]] | ||
=שאלות= | =שאלות= | ||
| + | |||
==מטריצות== | ==מטריצות== | ||
גרסה מ־18:51, 26 ביולי 2011
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 ארכיון
- 3 שאלות
- 3.1 מטריצות
- 3.2 הוכחת שדה
- 3.3 כתיבת שיעורי הבית
- 3.4 ניסוח בשאלה 2.3
- 3.5 לא הבנתי את חוק הקיבוץ
- 3.6 וגם למרות שזה לא בשיעורים
- 3.7 תרגיל 2.3 ד-שאלה עם הסימנים
- 3.8 הגדרת קב׳ השלמים
- 3.9 סימון סכום
- 3.10 שדות
- 3.11 3.1 סעיף ב
- 3.12 ??????????????????
- 3.13 אוסף שורשי היחיחדה
- 3.14 בעמוד 12 שאלה 1.6 (מז"א אסור להשתמש בחילוק אבל מותר צמצום?)
- 3.15 1.7
- 3.16 שאלה 3.1
- 3.17 שאלה 4.6 סעיף ב
- 3.18 הוכחה ש C הוא שדה
- 3.19 בענין של שדה בן 4 איברים
- 3.20 תודה לאוהד נ.ב יש לי עוד שאלה
- 3.21 בנוגע לשאלה 3.1 סעיף א
- 3.22 בקשר לשלוש משוואות עם שלושה נעלמים
- 3.23 שאלה
- 3.24 בקשר לתרגיל 1.8 עם ערכי a
- 3.25 בקשר ל4.6 אם אני עושה אינדוקציה אני מוכיח בעקרון רק עבור
- 3.26 4.6 סעיף ג'
- 3.27 ש"ב לשיעור שני בליניארית?
- 3.28 בקשר לשאלה 4.6
- 3.29 בקשר לשאלה 4.6
- 3.30 3.11 א
- 3.31 מאפיין ראשוני
- 3.32 2 שדות בעלי מאפיינים שווים אז השדה בעל מספר האיברים הגדול יותר מכיל את השני????
- 3.33 שיעורי בית
- 3.34 האם תרגילים 3+4 זה מה שיתנו בראשון ה- 24/07 או שזה שיעורים ליום שלישי?
- 3.35 תרגיל 2 שאלה 5.16
- 3.36 שאלה 3.2 עמוד 15
- 3.37 שאלה מתרגיל 2
- 3.38 בקשר לתרגיל 3.2
- 3.39 תרגיל 5.3
- 3.40 שאלה מתרגיל 3
- 3.41 6.20 ??????
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
מטריצות
בשאלה 1.7 בעמ 12 מבקשים מאיתנו למצוא מערכת משוואת עם כמות מסויימת של פתרונות,לא עברנו על כך בשיעור האם מישהו יוכל לעוזר לי בבקשה . איך אנו בודקים\מבקרים על כמות הפתרונות של מערכת משוואות ?
- כמות הפתרונות של מערכת משוואות הינה מספר האיברים בשדה בחזקת מספר המשתנים החופשיים. זה נכון מכיוון שכל משתנה חופשי יכול לקבל כל איבר מהשדה באופן בלתי תלוי באחרים. זה כמו לשאול כמה אפשרויות קיימות למצב 3 נורות כאשר כל אחד יכולה להיות דולקת או כבוייה (התשובה היא 2 בחזקת שלוש במקרה זה...) --ארז שיינר 20:35, 18 ביולי 2011 (IDT)
- לא מצויין גם באיזה שדה הפתרונות צריכים להיות, ולא מצויין סוג מערכת המשוואות. אתה יכול להגדיר פולינום כמו x^49 = 1 שיש לו 49 פתרונות במרוכבים, או שני פולינומים שיש לכל אחד 7 פתרונות. יש כמובן עוד הרבה דרכים (יש גם מערכות לינאריות בעלות 49 פתרונות).
- הכוונה בשאלה הינה למערכת משוואות לינאריות בלבד --ארז שיינר 18:21, 20 ביולי 2011 (IDT)
הוכחת שדה
לא הבנתי איך מוכיחים ששדה קיים. הבעיה צצה בתרגיל 3.1 אבל אשמח גם להסבר בכלליות.
גניה שנדלוב
תשובה: (לא מתרגל), למדת את התנאים שחייבים להתקיים בשדה, תעברי תנאי אחרי תנאי ותוכיחי שכולם מתקיימים.
שאומרים להוכיח שקבוצה מסויימת לא שדה מספיק להביא דוגמא נגדית אחת שקיימת? בקשר לשאלה 2.3 סעיף ב
תשובה: (לא מתרגל), דוגמא נגדית + הסבר ראוי יעשה את העבודה.
שאלה: נראה לי שהוא התכוון מה זה R*R לא למדנו מכפלה של שדות איך אני מכפיל שדה אחד בשני???
תשובה: (לא מתרגל), הכוונה בטח ל- RxR וזוהי מכפלה קרטזית שיוצרת זוגות סדורים. אתה לא מכפיל שדות אל מכפיל קבוצות. לדוגמה: אם קבוצה X מכילה 13 איברים של ערכי קלפים { A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 } וקבוצה Y מכילה 4 איברים של סוג הקלף {♠, ♥, ♦, ♣}, אזי המכפלה הקרטזית של שתי הקבוצות היא קבוצת קלפי המשחק המוכרת לנו, בעלת 52 האיברים { (♣ ,A, ♠), (K, ♠), ..., (2, ♠), (A, ♥), ..., (3, ♣), (2) }.
כן אבל מה זה אומר על התרגיל עצמו איך אני משתמש בזה על קבוצות שלא נתון לי אף איבר בהם????
תשובה: (לא מתרגל), אני חושב שאתה מדבר על שאלה 3.1. הכוונה היא להגדיר מספר מרוכב כזוג סדור. אנו הרי מכירים את המספר המרוכב כ- a+bi אז בשאלה רוצים שתציג זאת כ- (a,b), זו הבנתי...
כן אבל היתכוונתי ל בת FxF את א הבנתי לבד
- אני לא בטוח מה השאלה, אבל אני אנסה להגיב. לא מוכיחים ששדה הוא קיים. ניתן להוכיח האם קבוצה מסויימת עם פעולות כפל וחיבור מסוימות היא אכן שדה. היא אכן שדה אם כל תכונות השדה מתקיימות. --ארז שיינר 20:41, 18 ביולי 2011 (IDT)
כתיבת שיעורי הבית
מה צריך לכתוב כאשר מגישים את שיעורי הבית? האם יש צורך לכתוב כל תרגיל בעמוד נפרד? או שרק להפריד ביניהם?
בשאלה 2.3 סעיף ד, הכוונה שם שזה הקטע עם mod או קבוצת השלמים 0,1,2,3? תודה
- אין צורך לכתוב כל תרגיל בדף נפרד, אך תקפידו להפריד בין התרגילים ולציין את מספר התרגיל.
- בשאלה 2.3: הפעולות הן מודולו 3. --לואי פולב 15:06, 18 ביולי 2011 (IDT)
ניסוח בשאלה 2.3
לא הבנתי את ניסוח הנתונים בסעיף ד שאלה 2.3 - אפשר להסביר אותו? תודה
תשובה: אני לא מתרגל, אבל למיטב הבנתי, נותנים לך איזשהו מערך ריק ומגדירים בו חלקים משדה z3, תסתכל
איזו השמה בוצעה לכל איבר במערך ותחליט האם ניתן להגדיר את המערך החדש כשדה או לא.
תודה לך אבל בעיקרון את הנקודה הזו הבנתי, השאלה שלי היא מה הסימון F:=Z3 אומר? האם ש ב F מספר איברים כמו ב z3 ? או זו אותה קבוצה? למה לא עברנו על סימונים כאלו בתירגולים?
תודה מראש
תשובה: (לא מתרגל) כמדומני הסימון אומר: "מעתה,F הוא Z3" (על כל המשתמע מכך), שים לב לשאר ההשמות וצור לעצמך את המערך החדש שהתקבל.
תודה רבה תשובתך עזרה לי מאוד!
לא הבנתי את חוק הקיבוץ
ואם הפשר לדעת מה זה מאפיין CHAR תודה
- מה יש לא להבין בחוק? לא הבנת את הכתב? תכתוב אותו פה, ותגיד מה לא מובן ונוכל לעזור. מאפיין של שדה הינו המספר הקטן ביותר של אחדות שסכומם הוא אפס. למשל, אם 1+1=0 אזי המאפיין של השדה הוא 2. --ארז שיינר 20:36, 18 ביולי 2011 (IDT)
וגם למרות שזה לא בשיעורים
אם משהו יכול להסביר מדוע כשCHAR שונה מ0 אז CHAR(F( הוא ראשוני תודה
תשובה: (לא מתרגל), אנסה לענות לשאלתך, ושוב, איני מתרגל אז קח את זה בערבון מוגבל.
char=מאפיין, המאפיין הוא בעצם כמה פעמים אני צריך להוסיף 1 על מנת להגיע לאפס. לדוגמא: בשדה z5 על מנת להגיע לאפס אני צריך להוסיף את הספרה 1 חמש פעמים: 1+1+1+1+1=0. תנסה ותראה שכל תוספת של 5 תיתן לך את האפס. ולכן המאפיין הוא 5. וזה תופס כמובן לכל מספר ראשוני אחר.
אנחנו נקבל שהמאפיין שווה לאפס במידה ומדובר במספר אינסופי של איברי הקבוצה. למשל בקבוצת הרציונליים, ככל שנוסיף אחדות רק נתרחק מהאפס.ולכן המאפיין הוא- אפס. יש מצב שהניסוח קצת לוקה, אבל זה הרעיון...
- אני כן מתרגל. התשובה לא מסבירה מדוע בכל שדה המאפיין הוא ראשוני, אלא רק למה הוא כזה במקרה של השדות שלמדנו. כמדומני שהוכחתם מדוע מאפיין הוא תמיד ראשוני בהרצאה (אני לא מתחמק מהשאלה, אני פשוט לא בטוח שאני יודע בעצמי). --ארז שיינר 20:38, 18 ביולי 2011 (IDT)
אתה צודק הוכחנו בהרצאה ועכשיו לשאלה אם המאפיין לא יהיה ראישוני אז יהיו מחלקי אפס בשדה
- אני חושב שיש לי מושג למה: באחד התרגילים התבקשנו להוכיח שבשדה עם מאפיין p ישנו תת שדה שאיזומורפי (בעל אותן תכונות) ל Zp. בהוכחה* אני לא השתמשתי בעובדה ש p ראשוני. אז אם נניח שלשדה F יש מאפיין פריק n, אזי קיים תת שדה בF שאיזומורפי למבנה Zn. וכמובן Zn יש מחלקי אפס ולכן ב F יש מחלקי אפס. (סתירה להנחה,
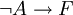 ולכן המאפיין חייב להיות ראשוני)
ולכן המאפיין חייב להיות ראשוני)
(*תסתכל על הקבוצה 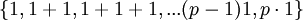 ותוכיח שהחיבור והכפל שלה זהים לשל Zp)
ותוכיח שהחיבור והכפל שלה זהים לשל Zp)
בפרט, אני רואה שמספיק(זה חלק מהפעולה שהיה צריך לעשות קודם) להוכיח שעבור כל m,n טבעיים מתקיים 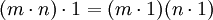 לכן אם המאפיין הוא m*n אז או שאחד מהגורמים שווה 0, וזה אומר שקיים מאפיין קטן יותר (סתירה), או שקיימים מחלקי 0 (סתירה) ולכן המאפיין לא יכול להיות פריק. --Ohadklein 18:09, 20 ביולי 2011 (IDT)
לכן אם המאפיין הוא m*n אז או שאחד מהגורמים שווה 0, וזה אומר שקיים מאפיין קטן יותר (סתירה), או שקיימים מחלקי 0 (סתירה) ולכן המאפיין לא יכול להיות פריק. --Ohadklein 18:09, 20 ביולי 2011 (IDT)
(לא מתרגל) חשבתי על זה ובהנחה שהמאפיין סופי ופריק, אפשר להוכיח שקיים מאפיין ראשוני קטן יותר לאותו שדה. כשאחזור אני אפרט את ההוכחה שלי.
תרגיל 2.3 ד-שאלה עם הסימנים
לא הבנתי מה זה אומר הסימנים 1F:=2Z3 0F=1Z3 לפי מה שאני הבנתי זה אומר ש2Z3 אמור לתפקד כאיבר ניטרלי בכפל ו1Z3 בחיבור אבל 2*2=4mod3=1 ו1+1=2 אז הם לא מתפקדים כמו מה שאני חושב אם מישהו יודע מה משמעות הסימונים שיגיד
- הם אמורים לתפקד באופן מסויים אם זה אכן שדה. לא קובעים לך את העובדה שזה שדה אלא שואלים אותך. --ארז שיינר 20:38, 18 ביולי 2011 (IDT)
הגדרת קב׳ השלמים
בשאלה 2.3 ב, איך אנחנו אמורים להוכיח שההופכי של 2 (לדוגמא) הוא לא שלם, אם בכלל לא הגדרנו את קבוצת השלמים? (אפשר לוותר על הפורמליות שם?)--22:45, 18 ביולי 2011 (IDT)
תשובה: (לא מתרגל), אני חושב שאפשר לעשות דבר כזה:
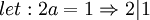 וזה כמובן לא נכון.
אפשר גם להסתכל על זה mod 2 ובטח לא מושג שוויון. --Ohadklein 00:19, 19 ביולי 2011 (IDT)
וזה כמובן לא נכון.
אפשר גם להסתכל על זה mod 2 ובטח לא מושג שוויון. --Ohadklein 00:19, 19 ביולי 2011 (IDT)
- לא הבנתי את מה שעשית, ונראה לי שאסור להשתמש בmod כי הכוונה היא לשדה עם הפעולות הרגילות.
תשובה: (לא מתרגל), mod זו פעולה ב Z, ב Zp היא פועלת אוטומטית. אולי אפשר להגיד גם שמכיוון ש a*2 מונוטונית אז מספיק לבדוק את ערכי הפונקציה עבור a = 0,1 ולראות שהיא לא שווה 1.
סימון סכום
אם יש לי את הקבוצה A, האם ניתן לסמן (Σ(A כסכום כל האיברים ב A, או שאני חייב להגדיר אינדקס שרץ מ 1 עד גודל הקבוצה?
- חייבים להגדיר אינדקס, אנחנו נלמד בעתיד שעבור קבוצות אינסופיות הסימון הזה יהיה מאד בעייתי. כלומר
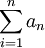 כאשר
כאשר 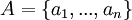 --ארז שיינר 07:19, 19 ביולי 2011 (IDT)
--ארז שיינר 07:19, 19 ביולי 2011 (IDT)
יש לי הערה: בסיכום http://www.math-wiki.com/index.php?title=88-101_%D7%97%D7%A9%D7%99%D7%91%D7%94_%D7%9E%D7%AA%D7%9E%D7%98%D7%99%D7%AA יש משפט "אומרים שקבוצת וקטורים...", אם אני לא טועה זו הגדרה של קבוצה שאינה תלויה לינארית.
- צודק, תוקן. --ארז שיינר 06:50, 19 ביולי 2011 (IDT)
שדות
לא הבנתי מה צריך להוכיח בשאלה 3.11 סעיף א'.
- להוכיח שקיים שורש יחידה (
![\sqrt[n]{1}](/images/math/a/5/a/a5a1bedf31964af3498c3ed01de7177c.png) ) כך שכל החזקות שלו נותנות את כל שורשי היחידה מסדר n. --ארז שיינר 06:53, 19 ביולי 2011 (IDT)
) כך שכל החזקות שלו נותנות את כל שורשי היחידה מסדר n. --ארז שיינר 06:53, 19 ביולי 2011 (IDT)
כשאומרים מסדר n הכוונה היא שאנחנו מוגבלים עד z^n=1 או שמותר לנו להשתמש בשורש יחידה מהצורה z^(n^2)=1 ?
שורשי היחידה מסדר n זה אומר כל ה z שמקיימים z^n = 1, לא יותר ולא פחות (מה שאתה אמרת אלו שורשי היחידה מסדר n^2).
3.1 סעיף ב
מה זה אומר FXF ? ואיך ניתן להוכיח שזה לא שדה ? בעזרת איזה תכונה של שדה ניתן להוכיח שFXF אינו שדה בגלל תכונתו a*a+1=0 ?
- FXF הינו קבוצה של זוגות סדורים של איברים מF; למשל
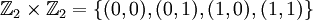 . כמו כן, מגדירים על הקבוצה הזו כפל וחיבור כמו שהגדרנו במשפט אשר בדיוק מעל השאלה הזו. בהתחשב בכל ההגדרות הללו, יש לבדוק האם כל תכונות השדה מתקיימות ואם לא. --ארז שיינר 12:48, 19 ביולי 2011 (IDT)
. כמו כן, מגדירים על הקבוצה הזו כפל וחיבור כמו שהגדרנו במשפט אשר בדיוק מעל השאלה הזו. בהתחשב בכל ההגדרות הללו, יש לבדוק האם כל תכונות השדה מתקיימות ואם לא. --ארז שיינר 12:48, 19 ביולי 2011 (IDT)
אם לכל איבר ששייך לF מתקיים שהוא עצמו בריבע + 1 =0 אז כל האיברים שוים i ?
תשובה (לא מתרגל): כתוב שקיים איבר המקיים את התנאי, ולא כל האיברים מקיימים את התנאי. תסתכל מה קורה עם האיבר (i,1) כאשר i^2+1=0 (ו i איבר ב F כמובן).--Ohadklein 14:33, 19 ביולי 2011 (IDT)
איך אתה יודע איזה איברים מוכלים בF ?
תשובה (לא מתרגל): זה נתון שקיים a ב F המקיים a^2+1 = 0 אז אני פשוט קראתי לו i.
אם מציבים i הטענה נכונה..אבל היא נכונה רק עבור i
אבל אין שם מספר ראשוני של איברים ב FxF אז זה לא שדה לא??? כי מספר האיברים שם הוא מספר האיברים ב F בריבוע.... או שזה שדה אין סופי כמו המרוכבים???
תשובה (לא מתרגל): ברור שזה שדה אינסופי, הוא מכיל את Z, את Q, וגם קל להראות שהוא מכיל את {Q(i) = {a+bi|a,b in Q. אם עשית את 3.1 (א') הסעיף הזה אמור להיות קל.
את א הצלחתי זה היה קל אבל פה אין לי מושג מאיפה להתחיל.... אני הגעתי לזה שאם a^2+1=0 אז a הוא מחלק אפס... אבל שוב זה בשדה F איך אני מוכיח לגבי FxF??? וגם איך בנוי איבר ב fxf האם הוא בנוי כך a+bi??? או שהוא בנוי כך a+b ואיך אפשר לדעת???
לא, אתה לא הוכחת את זה, כי זה לא נכון. C מכיל את i והוא שדה(היית אמור להוכיח את זה ב 3.1א). 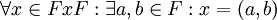 . יש תכונה שלא תעבוד לפחות עבור (i,1) א
.--Ohadklein 21:52, 19 ביולי 2011 (IDT)
. יש תכונה שלא תעבוד לפחות עבור (i,1) א
.--Ohadklein 21:52, 19 ביולי 2011 (IDT)
??????????????????
כדי להוכיח שF לא שדה ע"י תכונה צריך להסביר למה התכונה הזאת חייבת להיות בשדה ? (כמו למשל איברים נייטלים )
- ידוע לכולם מהן תכונות השדה, אין מה להסביר פה --ארז שיינר 18:55, 19 ביולי 2011 (IDT)
אוסף שורשי היחיחדה
מה זה?
![\sqrt[n]{1}](/images/math/a/5/a/a5a1bedf31964af3498c3ed01de7177c.png) --ארז שיינר 23:01, 19 ביולי 2011 (IDT)
--ארז שיינר 23:01, 19 ביולי 2011 (IDT)
בעמוד 12 שאלה 1.6 (מז"א אסור להשתמש בחילוק אבל מותר צמצום?)
הכוונה חילוק בין שורות אסור? וצמצום על שורה עצמה מותר?
תודה
- אסור לחלק כי אין הופכי לאף איבר. אבל מכיוון שאין מחלקי אפס, אם יש בשני צידי המשוואה משהו כפול 2 אז אפשר לצמצם את ה2 --ארז שיינר 23:06, 19 ביולי 2011 (IDT)
1.7
איך מוצאים את מערכת המשוואת ?
- זה התרגיל. כבר מישהו שאל בנושא, מומלץ לקרוא שאלות ותשובות של אחרים --ארז שיינר 23:03, 19 ביולי 2011 (IDT)
שאלה 3.1
מה הכוונה בהגדרה של השדה ש-C=R*R, צריך להתייחס לכך כמספרים מרוכבים?
לפי מה שהבנתי הכוונה לזוגות סדורים (a,b) כך ש a,b שייכים ל R
שאלה 4.6 סעיף ב
האם חייבים להשתמש בסעיף א או שאם רוצים אפשר לא???
- פתחתי את החוברת ורשום שם "השתמש ב(א)". אז חייבים --ארז שיינר 18:06, 20 ביולי 2011 (IDT)
הוכחה ש C הוא שדה
איך אני מוכיח שיש איברים הופכיים ונגדיים ב-C?
- אתה מראה מיהו ההופכי \ הנגדי ל (a,b).
- אבל קודם אני צריך להוכיח שיש בכלל הופכי\ נגדי ל (a,b) לא?
- אם אתה מראה מיהו, בין היתר הראת שקיים כזה. כלומר, אם מצאת לכל איבר (a,b) איבר (c,d) כך שסכומם הוא אפס, מצאת נגדי והוא אכן קיים. --ארז שיינר 18:19, 20 ביולי 2011 (IDT)
בענין של שדה בן 4 איברים
אני יודע ששנים ממנו צריכים להיות 1 ו0 כי הם איברים ניטרלים לחיבור ולכפל בהתאמה ולכן הם צריכים להיות בשדה אבל מה באופן עקרוני צריכים שאר המספרים להיות והאם פה החיבור והכפל זה בMOD4 או שזה רק בשדה סגור? נץב הסתכלתי באנרטנט וראיתי שזה משהו שקשור למתמטיקאי בשם גלאון וזה לא בקורס בסיסי אז עדיין לעשות את השאלה?
- זו שאלה למחשבה, אתה לא חייב לעשות. כן, המרצה הזכיר שזה קורס לא-בסיסי בחבורות גלואה אם אני לא טועה. בכל מקרה, זה תרגיל פשוט יחסית כי אם תנסה להגדיר טבלה שמציגה את הקשר בין האיברים, הרוב המוחלט של הטבלה תהיה מלאה מהגדרות ומזהויות בסיסיות, כמו כן לכל איבר מתקיים a+a = 0 כי a*1+a*1 = a*(1+1) = a*0 = 0. עשיתי את התרגיל שוב, השתמשתי בכל התכונות שלמדתי משיעורי הבית, הטבלאות נקבעות באופן יחיד.--Ohadklein 19:17, 20 ביולי 2011 (IDT)
תודה לאוהד נ.ב יש לי עוד שאלה
כשאמרו לי C:=r*r זה מתכווון שהאיברים במרוכיבים?
כן דרך אגב אוהד עוזר פה לכולם הוא סבבה :)
בנוגע לשאלה 3.1 סעיף א
רשמת שבכדי להוכיח שיש איברים נגדיים / הופכיים יש למצוא אותם לפני כן, באיזו דרך ניתן לעשות זאת?(בעזרת שתי משוואות עם ארבעה נעלמים הגעתי לa+c=0, b+d=0 ומכאן אני תקוע)
- שים לב, אלה לא 4 נעלמים, אלא 2. שכן (a,b) הוא איבר מסויים שאתה מחפש לו נגדי, ולכן a,b הם פרמטרים בלבד. --ארז שיינר 20:06, 20 ביולי 2011 (IDT)
בקשר לשלוש משוואות עם שלושה נעלמים
מה התנאים לפתרון אחד? אין סוף פתרונות? ואין פתרון?
- בצורה המדורגת
- אם יש שורת סתירה (כלומר שורת אפסים במטריצת המקדמים, ומספר שונה מאפס בעמודת הקבועים) אזי אין פתרון
- אם כל המשתנים תלויים (יש איבר פותח בעמודה של כל משתנה) אזי יש פתרון יחיד
- אחרת, יש מספר פתרונות כמספר האיברים בשדה בחזקת מספר המשתנים החופשיים.
- --ארז שיינר 21:25, 20 ביולי 2011 (IDT)
וד"א איך נרשמים פה?
- למעלה משמאל, כניסה לחשבון ואז לינק להרשמה --ארז שיינר 21:25, 20 ביולי 2011 (IDT)
שאלה
בשאלה 3.11 לא בדיוק הבנתי מה צריך להוכיח והאם שורשי היחידה הכוונה ל-z^n=1 בשאלה 4.6 אני לא כל כך מבין את נוסחת הבינום של ניטון ואיך אפשר להיעזר בה לפתרון א'
לא הבנתי כ"כ את השאלה.
את 4.6 א אפשר לפתור עם נוסחאת הבינום של ניוטון שהרי מתקיים 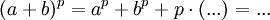 מכאן זה שטויות.
אגב, חשבתי על עוד הוכחה מגניבה ב Zp לסעיף ב': למדנו בשיעור ש
מכאן זה שטויות.
אגב, חשבתי על עוד הוכחה מגניבה ב Zp לסעיף ב': למדנו בשיעור ש 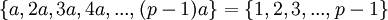 ולכן עכשיו נכפול את כל איברי הסדרה, נצמצם !(p-1) משני האגפים ונקבל
ולכן עכשיו נכפול את כל איברי הסדרה, נצמצם !(p-1) משני האגפים ונקבל 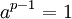 --Ohadklein 20:57, 20 ביולי 2011 (IDT)
--Ohadklein 20:57, 20 ביולי 2011 (IDT)
אוהד לא הבנתי את הפיתרון שלך למה זה שווה הרי הכפלת את כול השדה ב a???
בקשר לתרגיל 1.8 עם ערכי a
אם יוצא שעבור ערך מסויים בשורה 3 נגיד זה יוצא אינסוף פתרונות ובשורה אחרת זה יוצא אין פתרון אז מה עושים?
תודה
- פתרון הוא הצבה שמקיימת את כל המשוואות. אין כזה דבר שורת אינסוף פתרונות. ראה תשובה שתי שאלות מעליך --ארז שיינר 07:48, 21 ביולי 2011 (IDT)
הוא אמר שגם ככה אין דבר כזה אינסוף פיתרונות כי בשדות אין דבר כזה איןנסוף זאת אומרת שיש מספר סופי של פיתרונות אבל הוא גבוה נכון??
אבל אנחנו מדברים על שדה אינסופי (שהמאפיין שלו הוא 0) ולכן יכולים להיות אינסוף פתרונות.
בקשר ל4.6 אם אני עושה אינדוקציה אני מוכיח בעקרון רק עבור
מספרים שלמים ומה אם המספרים הלא שלמים?
אתה נדרש להוכיח את זה ב Zp...
חברה איפה הש"ב של שיעור שני??
4.6 סעיף ג'
איך אני יכול להוכיח בכלל שהשדה מכיל בתוכו את Zp לא נתון לי כלום על F חוץ מאשר המאפיין שלו (איך ניתן לקשר בין המאפיין לבין האיברים)
אני לא מבין בכלל מה ההבדל בין Zp לבין F שמקיים char(F)=p .. הרעיון הוא שבF יש גם מספרים לא שלמים?
- הכוונה בשאלה היא שתראה שיש p איברים בתוך השדה שהיחסים בינהם זהים ליחסים בZp (מבחינת חיבור וכפל כמובן). זה אותה גברת בשינוי אדרת. בשדה כללי ממאפיין p יכולים להיות יותר מ-p איברים... --109.65.34.186 21:17, 21 ביולי 2011 (IDT)
ש"ב לשיעור שני בליניארית?
איפה אני יכול למצוא את שיעורי הבית מהיום ה 21.7
- תמיד בדף התרגילים. הם עלו עכשיו לאתר. --ארז שיינר 08:31, 22 ביולי 2011 (IDT)
בקשר לשאלה 4.6
איך יתכן שיש מאפיין P בשדה הרי זה אומר ש: 1XP=0 כלומר יש מחלקי אפס
- p עצמו הוא אפס במקרה זה ואין הגדרה באמת לאחד כפול p --ארז שיינר 15:17, 22 ביולי 2011 (IDT)
בקשר לשאלה 4.6
איך יתכן שיש מאפיין P בשדה הרי זה אומר ש: 1XP=0 כלומר יש מחלקי אפס
3.11 א
הבנתי שאם התנאי לא מתקיים אז לכל פתרון קיים מספר טבעי k קטן מ-n שעבורו מתקיים z בחזקת k =1 איך אני ממשיכה?
מאפיין ראשוני
איך יכול ליהיות שדה ממאפיין ראשוני עם יותר איברים מהמאפיין, אפשר דוגמא לשדה כזה?
- אוסף הזוגות הסדורים
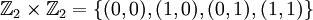 מכיל 4 איברים שונים, איבר האפס הוא (0,0) איבר היחידה הוא (1,0), איבר היחידה ועוד איבר היחידה שווה לאפס (ולכן המאפיין הוא 2). שימו לב שהכפל מוגדר כמו כפל מעל המרוכבים
מכיל 4 איברים שונים, איבר האפס הוא (0,0) איבר היחידה הוא (1,0), איבר היחידה ועוד איבר היחידה שווה לאפס (ולכן המאפיין הוא 2). שימו לב שהכפל מוגדר כמו כפל מעל המרוכבים 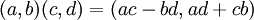 (זה מקרה פרטי של שאלה 3.1) --ארז שיינר 15:28, 22 ביולי 2011 (IDT)
(זה מקרה פרטי של שאלה 3.1) --ארז שיינר 15:28, 22 ביולי 2011 (IDT)
2 שדות בעלי מאפיינים שווים אז השדה בעל מספר האיברים הגדול יותר מכיל את השני????
לא, כי אחד מהם עשוי להיות גדול מהשני. לדוגמא, הממשיים אינם מוכלים ברציונאליים
- התכוונתי אם יש לי שדה עם k איברים שהמאפיין n ושדה אחר בעל k*2 איברים שגם המאפיין הוא n גם
תודה ארז
שיעורי בית
כתוב בשיעורים - מעמ 20 והלאה תרגילים 5.3 5.6 וכו אך אין אותם ...
5.3 נמצא בעמ 19 -זה מה שצריך לעשות ?
- כן, זה כנראה 20 בacrobat... --ארז שיינר 18:27, 22 ביולי 2011 (IDT)
האם תרגילים 3+4 זה מה שיתנו בראשון ה- 24/07 או שזה שיעורים ליום שלישי?
האם תרגילים 3+4 זה מה שיתנו בראשון ה- 24/07 או שזה שיעורים ליום שלישי?
- 3+4 הם התרגילים שתצטרכו להגיש בשבוע הבא (ולא הקרוב) --ארז שיינר 19:07, 23 ביולי 2011 (IDT)
תרגיל 2 שאלה 5.16
עפ"י ההוכחה שלי לתרגיל זה, יוצא ש A1^n = I (כאשר I זו מטריצת היחידה מסדר n)
באמת בדקתי את הטענה עבור n = 2, 3 ומתקיים מה שכתבתי לעיל. לעומת זאת, בשאלה כתוב שמתקיים A1^n = O וכמו שציינתי, זה לא מה שיוצא לי.
מה שכן, מתקיים לפי דעתי (Am = A1^m = A1^(m mod n. איפה הטעות שלי? --Ohadklein 01:12, 24 ביולי 2011 (IDT)
- כנראה שהטעות שלך היא במבנה המטריצה, כי לא יכול להיות שזה יוצא מטריצה היחידה. לדוגמא עבור n=2 מתקיים ש
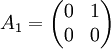 ואכן מתקיים
ואכן מתקיים 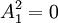 --ארז שיינר 11:18, 24 ביולי 2011 (IDT)
--ארז שיינר 11:18, 24 ביולי 2011 (IDT)
אויש, כן... הבעיה הייתה שחשבתי שהאחדים נמצאים גם על המשך האלכסון(מצד שמאל של המטריצה)... במקרה כזה התנאי שלי לקיום 1 במיקום i,j היה (i+k = j (mod n... אבל צריך להוריד את ה mod...--Ohadklein 16:04, 24 ביולי 2011 (IDT)
שאלה 3.2 עמוד 15
לא ברור מה צריך לעשות. האם צריך לחשב את המטריצה או להגיד מאיזה סדר היא צריכה להיות. תודה מראש
- לחשב את המטריצה במפורש, כאמור בשאלה, ע"י שימוש במשוואות לנאריות על אייברי המטריצה. (עדי ניב)
שאלה מתרגיל 2
בשאלה 5.16 בעמוד 21 איך נראית המטריצה? ומה הכוונה "כל ערכי האלכסון הk מעל האלכסון הראשי"?
- האלכסון הראשי הוא האלכסון של כל הרכיבים ה-i,i ולכן האלכסון ה k מעל הראשי הוא האלכסון של כל הרכיבים ה- i,i+k .
- ולכן מבקשים בעצם להראות שאם ניקח מטריצה עם אחדים באלכסון שמעל הראשי ואפסים מחוץ לו (
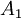 ) ונעלה אותה בחזקת k, אלכסון האחדים "יטפס" מעלה לאלכסון ה-k מעל הראשי. (עדי ניב)
) ונעלה אותה בחזקת k, אלכסון האחדים "יטפס" מעלה לאלכסון ה-k מעל הראשי. (עדי ניב)
בקשר לתרגיל 3.2
מה פירוש שימוש במשוואות לינאריות על איברי המטריצה??
- ניתן להסתכל על איברי המטריצה אותה מנסים למצוא כעל נעלמים. לאחר מכן, יש להבין אילו משוואות יש צורך לבנות ולפתור על מנת למצוא את המטריצה הנעלמת. --לואי פולב
תרגיל 5.3
לא הבנתי מה אני אמור לעשות להוכיח? כבר הבנתי תודה
שאלה מתרגיל 3
בעמוד 33 שאלה 1.1וחצי מותר להוכיח שהם מרחבים וקטוריים ע"פ הקריטריון המקוצר או שצריך להוכיח את כל התכונות?
- הקריטריון המקוצר תקף רק לתת מרחב; על מנת להוכיח שקבוצה היא מרחב ווקטורי יש לבדוק את כל האקסיומות. --לואי פולב
6.20 ??????
איך אפשר להשתמש בסעיף א' כדי להוכיח את השאלה הקודמת ??
- זה בדיוק סעיף ב' --ארז שיינר 21:37, 26 ביולי 2011 (IDT)
- כן הבנתי, אבל אני לא מבין איך עושים את זה, אם הוכחנו שA מאפס את הפונקציה וA הוא איבר כללי a b c d זה לא אומר שכל מטריצה מאפסת אותה ?
- הפולינום הזה משתנה כתלות במטריצה, הרי הוא מכיל את העקבה ואת דלתא. העובדה שהפונקציה הזו מאפסת את A גוררת משהו. שימו לב רק לדרך בה מציבים מטריצה בפולינום:
- יהי פולינום
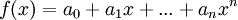 ותהי
ותהי 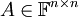 מטריצה ריבועית, אזי
מטריצה ריבועית, אזי 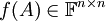 הנה המטריצה
הנה המטריצה 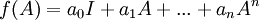 --ארז שיינר 21:48, 26 ביולי 2011 (IDT)
--ארז שיינר 21:48, 26 ביולי 2011 (IDT)