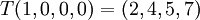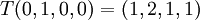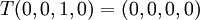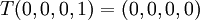הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/10"

גרסה מ־16:35, 14 באוגוסט 2011

מציאת גרעין ותמונה בעזרת מטריצה מייצגת

הגדרה. יהי V מ"ו ויהי U תת מרחב שלו. יהי B בסיס לV. אזי מרחב הקואורדינטות של U לפי B הינו $[U]_B:=\{[u]_B:u\in U\}$ . כפי שלמדנו העתקת הקואורדינטות הינה איזומורפיזם ולכן בהנתן מרחב קואורדינטות קל למצוא את המרחב המקורי.

תרגיל. תהי A מטריצה ו-f פונקציה המוגדרת על ידי כפל במטריצה f(v)=Av. מצא את הגרעין ואת התמונה של f.

פתרון. קל לראות שהגרעין הינו 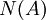$N(A)$ והתמונה הינה 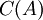$C(A)$ (שכן Av הינו צירוף לינארי של עמודות A עם הסקלרים מv).

מסקנה. תהי T העתקה לינארית מV לW, עם E וF בסיסים בהתאמה. אזי מרחב הקואורדינטות של הגרעין הינו $[kerT]_E=\{[v]_E:Tv=0\}=\{[v]_E:[Tv]_F=[T]^E_F[v]_E=0\}=N([T]^E_F)$ . מרחב הקואורדינטות של התמונה הינו $[ImT]_F=\{[Tv]_F:v\in V\}=\{[Tv]_F=[T]^E_F[v]_E:[v]_E\in\mathbb{F}^n\}=C([T]^E_F)$

אלגוריתם למציאת גרעין ותמונה של העתקה לפי המטריצה המייצגת

מצא מטריצה מייצגת $A=[T]^E_F$
מצא את מרחבי הקואורדינטות של הגרעין והתמונה $N(A)=[kerT]_E,C(A)=[ImT]_F$
העבר חזרה את מרחבי הקואורדינטות לצורה המקורית (ע"י כפל הסקלרים מהקואורדינטות באיברי הבסיס)

תרגיל. (6.14)

א. מצא בצורה מפורשת העתקה לינארית 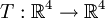$T:\mathbb{R}^4\rightarrow \mathbb{R}^4$ כך שמתקיים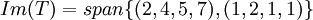 $Im(T)=span\{(2,4,5,7),(1,2,1,1)\}$

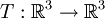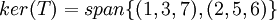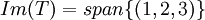
ב. מצא בצורה מפורשת העתקה לינארית $T:\mathbb{R}^3\rightarrow \mathbb{R}^3$ כך ש $ker(T)=span\{(1,3,7),(2,5,6)\}$ וגם $Im(T)=span\{(1,2,3)\}$

פתרון.

א. פה אין דרישות רבות לתרגיל, רק דורשים תמונה מסוימת. אם כן, נשלח כל וקטור במרחב לצירוף לינארי של הוקטורים הנתונים, ונדאג לעבור על כל הצירופים האפשריים. 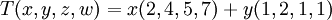$T(x,y,z,w)=x(2,4,5,7)+y(1,2,1,1)$ . קל לראות שהתמונה היא בדיוק כפי שנדרש ע"י הכלה דו כיוונית.

דרך נוספת לפתרון: ניתן להגדיר את T לפי משפט ההגדרה באופן הבא:

T(1,0,0,0)=(2,4,5,7)

T(0,1,0,0)=(1,2,1,1)

T(0,0,1,0)=(0,0,0,0)

T(0,0,0,1)=(0,0,0,0)

לאחר מכן קל למצוא את המטריצה המייצגת ולהכפיל אותה בווקטור כללי (כך ששתתקבל הצורה המפורשת של ההעתקה)

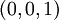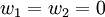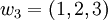ב. נשלים את הוקטורים הנתונים לבסיס ע"י הוקטור $(0,0,1)$ . נסמן $w_1=w_2=0$ ונסמן $w_3=(1,2,3)$ . נמצא את העתקה במפורש לפי האלגוריתם. ברור שהקבוצה הדרושה מוכלת בגרעין, משיקולי מימד היא שווה לו (כי התמונה ממימד אחד לפחות).

תרגיל. (6.16) תהי 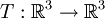$T:\mathbb{R}^3\rightarrow\mathbb{R}^3$ העתקה לינארית המוגדרת על ידי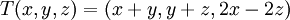 $T(x,y,z)=(x+y,y+z,2x-2z)$

א. מצא בסיס לגרעין ולתמונה של T

ב. מצא בסיס סדור E ל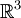 $\mathbb{R}^3$ כך ש $[T]^E_E=\begin{pmatrix} 0 & 0 & 0 \\ 0 & * & * \\ 0 & * & * \end{pmatrix}$

פתרון.

א. נמצא מטריצה מייצגת לפי הבסיס הסטנדרטי. נראה מה התמונה של איברי הבסיס:

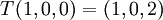
$T(1,0,0)=(1,0,2)$

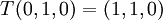
$T(0,1,0)=(1,1,0)$

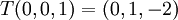
$T(0,0,1)=(0,1,-2)$

ולכן

$[T]=[T]^S_S=\begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 2 & 0 & -2\end{pmatrix}$

מעל הבסיס הסטנדרטי, מרחב הקואורדינטות של תת מרחב U הוא U בעצמו. ולכן גרעין ההעתקה הינו $N([T])$ ותמונת ההעתקה הינה $C([A])$ .

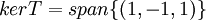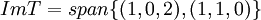
יוצא ש $kerT=span\{(1,-1,1)\}$ ויוצא $ImT=span\{(1,0,2),(1,1,0)\}$

ב. במקרה שלנו, יצא ש 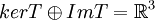$kerT \oplus ImT = \mathbb{R}^3$ . נגדיר את E להיות בסיס המורכב מאיחוד הבסיסים של הגרעין והתמונה, ונביט במטריצה המייצגת את ההעתקה לפי בסיס זה. מכיוון שהוקטור הראשון הוא בסיס לגרעין, התמונה שלו היא אפס וכך גם הקואורדינטות.

כמו כן, נביט בקואורדינטות של כל וקטור התמונה. מכיוון שזהו סכום ישר, יש הצגה יחידה של וקטור בתמונה לפי הבסיס שלנו E. אבל, גם יש לו הצגה יחידה לפי הבסיס לתמונה (שהוא מוכל בE) ולכן הקואורדינטות לפי וקטור הגרעין חייבות להיות אפס, כלומר השורה הראשונה הינה שורת אפסים.

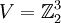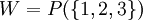תרגיל. יהיו $V=\mathbb{Z}_2^3$ ו $W=P(\{1,2,3\})$ מ"ו מעל השדה 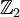$\mathbb{Z}_2$ . (זכרו כי החיבור הוקטורי בקבוצת החזקה הינו הפרש סימטרי). תהי העתקה לינארית המוגדרת לפי משפט ההגדרה על ידי

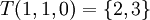
$T(1,1,0)=\{2,3\}$

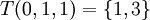
$T(0,1,1)=\{1,3\}$

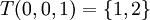
$T(0,0,1)=\{1,2\}$

מצא את הגרעין ואת התמונה של ההעתקה.

פתרון.

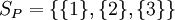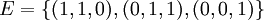שוב אנו נתקלים במרחב יחסית חדש ואנו צריכים למצוא לו בסיס סנדרטי. הבסיס הסטנדרטי למרחב קבוצת החזקה הוא באופן טבעי הנקודונים, שכן כל תת קבוצה הינה הפרש סימטרי של הנקודונים של האיברים שבה. אם כן הבסיס הסטנדרטי הינו $S_P=\{\{1\},\{2\},\{3\}\}$ . נגדיר בסיס $E=\{(1,1,0),(0,1,1),(0,0,1)\}$ .

לכן המטריצה המייצגת הינה: $[T]^E_{S_P}=\begin{pmatrix}0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0\end{pmatrix}$

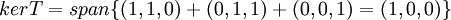נמצא את הגרעין. $[kerT]_E=N([T]^E_{S_P})=span\{(1,1,1)\}$ . אלו הקואורדינטות של הבסיס, ולכן הבסיס הוא הצירופים הלינאריים של איברי E עם הקואורדינטות הנ"ל כלומר $kerT = span\{(1,1,0)+(0,1,1)+(0,0,1)=(1,0,0)\}$ . קל מאד לראות שהגרעין שונה ממרחב הקואורדינטות שלו.

נמצא את התמונה. $[ImT]_{S_P}=C([T]^E_{S_P})=span\{(0,1,1),(1,0,1)\}$ .

אם $[v]_{S_P}=(0,1,1)$ אזי

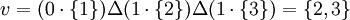
$v=(0\cdot\{1\})\Delta (1\cdot\{2\}) \Delta (1\cdot\{3\})=\{2,3\}$

באופן דומה 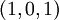$(1,0,1)$ תואם ל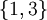 $\{1,3\}$

לסיכום 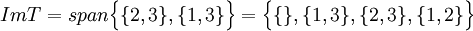$ImT=span\Big\{\{2,3\},\{1,3\}\Big\}=\Big\{\{\},\{1,3\},\{2,3\},\{1,2\}\Big\}$ וזו התמונה של ההעתקה.

@@ שורה 20: / שורה 20: @@
 א. מצא בצורה מפורשת העתקה לינארית <math>T:\mathbb{R}^4\rightarrow \mathbb{R}^4</math> כך שמתקיים <math>Im(T)=span\{(2,4,5,7),(1,2,1,1)\}</math>
+ב. מצא בצורה מפורשת העתקה לינארית <math>T:\mathbb{R}^3\rightarrow \mathbb{R}^3</math> כך ש <math>ker(T)=span\{(1,3,7),(2,5,6)\}</math> וגם <math>Im(T)=span\{(1,2,3)\}</math>
+'''פתרון.'''
+א. פה אין דרישות רבות לתרגיל, רק דורשים תמונה מסוימת. אם כן, נשלח כל וקטור במרחב לצירוף לינארי של הוקטורים הנתונים, ונדאג לעבור על כל הצירופים האפשריים. <math>T(x,y,z,w)=x(2,4,5,7)+y(1,2,1,1)</math>. קל לראות שהתמונה היא בדיוק כפי שנדרש ע"י הכלה דו כיוונית.
 דרך נוספת לפתרון: ניתן להגדיר את T לפי משפט ההגדרה באופן הבא:
@@ שורה 28: / שורה 36: @@
 לאחר מכן קל למצוא את המטריצה המייצגת ולהכפיל אותה בווקטור כללי (כך ששתתקבל הצורה המפורשת של ההעתקה)
-ב. מצא בצורה מפורשת העתקה לינארית <math>T:\mathbb{R}^3\rightarrow \mathbb{R}^3</math> כך ש <math>ker(T)=span\{(1,3,7),(2,5,6)\}</math> וגם <math>Im(T)=span\{(1,2,3)\}</math>
-'''פתרון.'''
-א. פה אין דרישות רבות לתרגיל, רק דורשים תמונה מסוימת. אם כן, נשלח כל וקטור במרחב לצירוף לינארי של הוקטורים הנתונים, ונדאג לעבור על כל הצירופים האפשריים. <math>T(x,y,z,w)=x(2,4,5,7)+y(1,2,1,1)</math>. קל לראות שהתמונה היא בדיוק כפי שנדרש ע"י הכלה דו כיוונית.
 ב. נשלים את הוקטורים הנתונים לבסיס ע"י הוקטור <math>(0,0,1)</math>. נסמן <math>w_1=w_2=0</math> ונסמן <math>w_3=(1,2,3)</math>. נמצא את העתקה במפורש לפי האלגוריתם. ברור שהקבוצה הדרושה מוכלת בגרעין, משיקולי מימד היא שווה לו (כי התמונה ממימד אחד לפחות).

הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/10"

גרסה מ־16:35, 14 באוגוסט 2011

מציאת גרעין ותמונה בעזרת מטריצה מייצגת

אלגוריתם למציאת גרעין ותמונה של העתקה לפי המטריצה המייצגת

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים