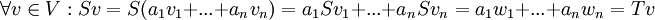הבדלים בין גרסאות בדף "משפט ההגדרה"
מתוך Math-Wiki
(←משפט ההגדרה) |
(←הוכחה) |
||
| שורה 13: | שורה 13: | ||
=הוכחה= | =הוכחה= | ||
| + | יהי <math>v\in V</math> אזי קיימת הצגה יחידה שלו לפי הבסיס B | ||
| + | |||
| + | ::<math>v=a_1v_1+...+a_nv_n</math>. | ||
| + | |||
| + | לכן, ניתן להגדיר היטב העתקה T על ידי | ||
| + | |||
| + | ::<math>Tv=a_1w_1+...+a_nw_n</math>. | ||
| + | |||
| + | |||
| + | קל מאד להראות כי T המוגדרת לעיל הינה העתקה לינארית וגם מקיימת את המשוואות במשפט (כלומר <math>Tv_i=w_i</math>). | ||
| + | |||
| + | |||
| + | נותר להוכיח כי T יחידה. אמנם, אם S העתקה לינארית המקיימת את המשוואות מהמשפט (כלומר <math>Sv_i=w_i</math>), מתקיים: | ||
| + | |||
| + | ::<math>\forall v\in V:Sv=S(a_1v_1+...+a_nv_n)=a_1Sv_1+...+a_nSv_n=a_1w_1+...+a_nw_n=Tv</math> | ||
| + | |||
| + | ולכן S=T. | ||
גרסה מ־18:35, 15 בספטמבר 2011
משפט ההגדרה
יהי V מ"ו נוצר סופית, ויהי 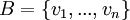 בסיס ל-V. יהי W מ"ו נוצר סופית ויהיו
בסיס ל-V. יהי W מ"ו נוצר סופית ויהיו 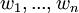 וקטורים כלשהם (לא בהכרח שונים)
וקטורים כלשהם (לא בהכרח שונים)
אזי קיימת העתקה לינארית יחידה 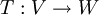 המקיימת:
המקיימת:
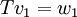

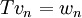
הוכחה
יהי 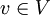 אזי קיימת הצגה יחידה שלו לפי הבסיס B
אזי קיימת הצגה יחידה שלו לפי הבסיס B
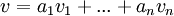 .
.
לכן, ניתן להגדיר היטב העתקה T על ידי
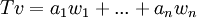 .
.
קל מאד להראות כי T המוגדרת לעיל הינה העתקה לינארית וגם מקיימת את המשוואות במשפט (כלומר 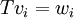 ).
).
נותר להוכיח כי T יחידה. אמנם, אם S העתקה לינארית המקיימת את המשוואות מהמשפט (כלומר 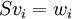 ), מתקיים:
), מתקיים:
ולכן S=T.