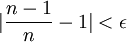הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/גבול"
(יצירת דף עם התוכן "===ההגדרה המדוייקת של סדרה=== בבדידה נלמד/למדנו את ההגדרה המדוייקת של [[88-195 בדידה לתיכוניסטי...") |
|||
| שורה 30: | שורה 30: | ||
כך שהחל ממנו והלאה (לכל <math>n>N_{\epsilon}</math>) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך <math>\epsilon</math> (<math>|a_n-L|<\epsilon</math>) [מתאים לו] | כך שהחל ממנו והלאה (לכל <math>n>N_{\epsilon}</math>) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך <math>\epsilon</math> (<math>|a_n-L|<\epsilon</math>) [מתאים לו] | ||
| + | |||
| + | ===דוגמאות=== | ||
| + | '''תרגיל.''' מצא את גבול הסדרה <math>\lim_{n\rightarrow\infty}\frac{n-1}{n}</math> | ||
| + | |||
| + | '''פתרון.''' מהתבוננות באיברים הראשונים של הסדרה אנו '''מנחשים''' שגבול הסדרה הינו 1. נוכיח זאת. | ||
| + | |||
| + | '''יהי אפסילון גדול מאפס'''. (הוכחה באינפי מתחילה בשורה זו לעיתים דחופות. מכיוון שההגדרות דורשות שתכונה מסוימת תתקיים '''לכל''' אפסילון, אם נוכיח אותה לאפסילון מבלי להתייחס לערך שלו, הוכחנו שהיא נכונה תמיד.) | ||
| + | |||
| + | כעת, אנו רוצים למצוא מקום בסדרה שהחל ממנו והלאה איברי הסדרה קרובים לאחד עד כדי אפסילון. כלומר: | ||
| + | |||
| + | ::<math>|\frac{n-1}{n}-1|<\epsilon</math> | ||
| + | |||
| + | נפתח את הביטוי. | ||
| + | |||
| + | ::<math>|\frac{n-1}{n}-1|=|\frac{-1}{n}|=\frac{1}{n}</math> | ||
| + | |||
| + | כעת, אנו מעוניינים כי יתקיים <math>\frac{1}{n}<\epsilon</math>, זה נכון אם"ם <math>n>\frac{1}{\epsilon}</math> | ||
| + | |||
| + | |||
| + | נבחר, אפוא, <math>N_{\epsilon}>\frac{1}{\epsilon}</math> כלשהו (מותר כיוון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל <math>n>N_{\epsilon}</math> מתקיים <math>n>N_{\epsilon}>\frac{1}{\epsilon}</math> ולכן איברי הסדרה קרובים ל-1 עד כדי אפסילון כפי שרצינו. | ||
גרסה מ־14:27, 17 באוקטובר 2011
ההגדרה המדוייקת של סדרה
בבדידה נלמד/למדנו את ההגדרה המדוייקת של פונקציה. סדרה הינה פונקציה מקבוצת הטבעיים אל קבוצה כלשהי. סדרה ממשית, למשל, הינה פונקציה מהטבעיים אל הממשיים.
באופן טבעי, התמונה של המספר הטבעי 1 נקראת האיבר הראשון של הסדרה, התמונה של 2 היא האיבר השני וכן הלאה.
גבול של סדרה
תהי סדרת מספרים ממשיים 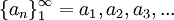 , (כך ש
, (כך ש 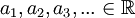 ).
).
לדוגמא:
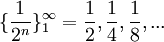
גבול של סדרה הוא נקודה ממשית אליה איברי הסדרה מתקרבים. לסדרה שלא מתקרבת לנקודה ספציפית אין גבול, למשל: 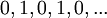 (לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
(לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
הגדרת הגבול
תהי  סדרה של מספרים ממשיים. אזי מספר ממשי
סדרה של מספרים ממשיים. אזי מספר ממשי 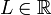 נקרא גבול הסדרה
נקרא גבול הסדרה  אם לכל
אם לכל 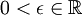 קיים
קיים 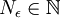 כך שלכל
כך שלכל 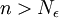 מתקיים
מתקיים 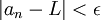 .
.
הסבר ההגדרה
נתרגם את זה למילים. למדנו ש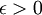 מודד אורך, מספר טבעי
מודד אורך, מספר טבעי 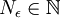 מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
נקודה L על ציר המספרים הממשיים היא גבול הסדרה 
אם לכל אורך (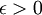 ) [סיר]
) [סיר]
קיים מקום בסדרה (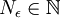 ) [מכסה]
) [מכסה]
כך שהחל ממנו והלאה (לכל 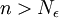 ) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך
) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך 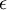 (
(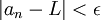 ) [מתאים לו]
) [מתאים לו]
דוגמאות
תרגיל. מצא את גבול הסדרה 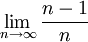
פתרון. מהתבוננות באיברים הראשונים של הסדרה אנו מנחשים שגבול הסדרה הינו 1. נוכיח זאת.
יהי אפסילון גדול מאפס. (הוכחה באינפי מתחילה בשורה זו לעיתים דחופות. מכיוון שההגדרות דורשות שתכונה מסוימת תתקיים לכל אפסילון, אם נוכיח אותה לאפסילון מבלי להתייחס לערך שלו, הוכחנו שהיא נכונה תמיד.)
כעת, אנו רוצים למצוא מקום בסדרה שהחל ממנו והלאה איברי הסדרה קרובים לאחד עד כדי אפסילון. כלומר:
נפתח את הביטוי.
כעת, אנו מעוניינים כי יתקיים 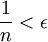 , זה נכון אם"ם
, זה נכון אם"ם 
נבחר, אפוא, 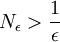 כלשהו (מותר כיוון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל
כלשהו (מותר כיוון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל 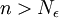 מתקיים
מתקיים  ולכן איברי הסדרה קרובים ל-1 עד כדי אפסילון כפי שרצינו.
ולכן איברי הסדרה קרובים ל-1 עד כדי אפסילון כפי שרצינו.