הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 8"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏הלמה של צורן)
שורה 6: שורה 6:
  
 
'''הלמה של צורן.''' תהי A קבוצה סדורה חלקית '''לא ריקה''' כך שלכל שרשרת המוכלת בA קיים חסם מלעיל מA. אזי קיים בA איבר מקסימלי (איבר שאין איבר שונה ממנו הגדול ממנו).
 
'''הלמה של צורן.''' תהי A קבוצה סדורה חלקית '''לא ריקה''' כך שלכל שרשרת המוכלת בA קיים חסם מלעיל מA. אזי קיים בA איבר מקסימלי (איבר שאין איבר שונה ממנו הגדול ממנו).
 +
  
 
הלמה של צורן שקולה ל'''אקסיומת הבחירה.''' תהי <math>\{A_i\}_i{\in I}</math> משפחה של קבוצות. אזי קיימת פונקציה <math>f:\{A_i\}_{i\in I}\rightarrow\bigcup_{i\in I}A_i </math> המקיימת <math>\forall i\in I:f(A_i)\in A_i</math>. במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה.
 
הלמה של צורן שקולה ל'''אקסיומת הבחירה.''' תהי <math>\{A_i\}_i{\in I}</math> משפחה של קבוצות. אזי קיימת פונקציה <math>f:\{A_i\}_{i\in I}\rightarrow\bigcup_{i\in I}A_i </math> המקיימת <math>\forall i\in I:f(A_i)\in A_i</math>. במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה.
שורה 12: שורה 13:
 
'''דוגמא.''' תהי <math>f:A\rightarrow B</math> פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f.
 
'''דוגמא.''' תהי <math>f:A\rightarrow B</math> פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f.
  
−
'''הוכחה.''' נציג את A כאיחוד אוסף המקורות של כל התמונות של הפונקציה <math>A=\bigcup_{b\in im(f)}f^{-1}\Big[\{b\}\Big]</math>. לפי אקסיומת הבחירה ניתן לבנות פונקציה  
+
'''הוכחה (באמצעות אקסיומת הבחירה).''' נציג את A כאיחוד אוסף המקורות של כל התמונות של הפונקציה <math>A=\bigcup_{b\in im(f)}f^{-1}\Big[\{b\}\Big]</math>. לפי אקסיומת הבחירה ניתן לבנות פונקציה  
 
<math>g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A</math> השולחת כל קבוצת מקורות לנציג כלשהו שלה.
 
<math>g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A</math> השולחת כל קבוצת מקורות לנציג כלשהו שלה.
  
 
נוכיח כי <math>h:=f|_{im(g)}</math> הינה חח"ע והתמונה שלה שווה לזו של f. נניח <math>h(a)=h(b)</math> לכן <math>a,b\in f^{-1}\Big[\{h(a)\}\Big]</math> אבל כל מקור של תמונה נשלח לנציג '''יחיד''' על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת.
 
נוכיח כי <math>h:=f|_{im(g)}</math> הינה חח"ע והתמונה שלה שווה לזו של f. נניח <math>h(a)=h(b)</math> לכן <math>a,b\in f^{-1}\Big[\{h(a)\}\Big]</math> אבל כל מקור של תמונה נשלח לנציג '''יחיד''' על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת.
 +
 +
 +
'''הוכחה (באמצעות הלמה של צורן).'''. נביט באוסף תתי הקבוצות של A כך שהצמצום של f עליהן חח"ע. קל להוכיח כי האיחוד הכללי של שרשרת באוסף זה גם שייך לאוסף, ולכן יש קבוצה מקסימלית שהצמצום של f עליה הינו חח"ע.
 +
 +
כיוון שזו קבוצה מקסימלית, לא ניתן להוסיף לה איברים נוספים ולהגדיל את התמונה, ומכאן ישנן שתי אופציות- הקבוצה המקסימלית היא A כולה (ואז f חח"ע וסיימנו) או, שלא קיים איבר נוסף בתמונה של f שלא קיבלנו כבר (ולכן התמונה של הצמצום זהה לתמונה של כל f כפי שרצינו).
 +
 +
  
  

גרסה מ־07:54, 13 באוגוסט 2012

חזרה למערכי התרגול

הלמה של צורן

הגדרה. קבוצה A אשר מוגדר עליה יחס סדר חלקי R נקראת קבוצה סדורה חלקית. תת קבוצה של קבוצה סדורה חלקית 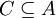C\subseteq A נקראת שרשרת אם R מהווה יחס סדר מלא על C.

הלמה של צורן. תהי A קבוצה סדורה חלקית לא ריקה כך שלכל שרשרת המוכלת בA קיים חסם מלעיל מA. אזי קיים בA איבר מקסימלי (איבר שאין איבר שונה ממנו הגדול ממנו).


הלמה של צורן שקולה לאקסיומת הבחירה. תהי 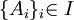\{A_i\}_i{\in I} משפחה של קבוצות. אזי קיימת פונקציה 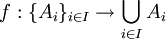f:\{A_i\}_{i\in I}\rightarrow\bigcup_{i\in I}A_i המקיימת 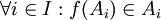\forall i\in I:f(A_i)\in A_i. במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה.


דוגמא. תהי 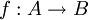f:A\rightarrow B פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f.

הוכחה (באמצעות אקסיומת הבחירה). נציג את A כאיחוד אוסף המקורות של כל התמונות של הפונקציה A=\bigcup_{b\in im(f)}f^{-1}\Big[\{b\}\Big]. לפי אקסיומת הבחירה ניתן לבנות פונקציה g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A השולחת כל קבוצת מקורות לנציג כלשהו שלה.

נוכיח כי 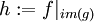h:=f|_{im(g)} הינה חח"ע והתמונה שלה שווה לזו של f. נניח 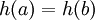h(a)=h(b) לכן a,b\in f^{-1}\Big[\{h(a)\}\Big] אבל כל מקור של תמונה נשלח לנציג יחיד על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת.


הוכחה (באמצעות הלמה של צורן).. נביט באוסף תתי הקבוצות של A כך שהצמצום של f עליהן חח"ע. קל להוכיח כי האיחוד הכללי של שרשרת באוסף זה גם שייך לאוסף, ולכן יש קבוצה מקסימלית שהצמצום של f עליה הינו חח"ע.

כיוון שזו קבוצה מקסימלית, לא ניתן להוסיף לה איברים נוספים ולהגדיל את התמונה, ומכאן ישנן שתי אופציות- הקבוצה המקסימלית היא A כולה (ואז f חח"ע וסיימנו) או, שלא קיים איבר נוסף בתמונה של f שלא קיבלנו כבר (ולכן התמונה של הצמצום זהה לתמונה של כל f כפי שרצינו).



תרגיל ממבחן תשס"ט מועד א' (ד"ר שי סרוסי וד"ר אלי בגנו). קבוצה נקראת "מגניבה" אם ההפרש בין כל שני איברים שונים בה אינו רציונאלי. הוכח כי קיימת קבוצה מגניבה C כך שלכל 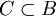C\subset B מתקיים כי B אינה מגניבה. כמו כן, הוכח שמתקיים שלכל איבר שאינו ב-C יש איבר מ-C אשר ההפרש בינהם רציונאלי.

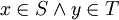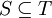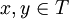הוכחה. נביט באוסף הקבוצות המגניבות וביחס ההכלה. לכל שרשרת של קבוצות מגניבות מתקיים כי האיחוד הכללי שלהן הינו קבוצה מגניבה. אמנם, אם x,y באיחוד הכללי אזי קיימות קבוצות בשרשרת S,T כך ש x\in S \and y\in T. מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי S\subseteq T ולכן x,y\in T ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו.

אם כן, האיחוד הכללי הינו חסם מקסימלי של השרשרת (כי הוא מכיל את כל הקבוצות בשרשרת) מתוך אוסף הקבוצות המגניבות, ולכן לפי הלמה של צורן קיימת קבוצה מגניבה מקסימלית ביחס להכלה. זה אומר שכל קבוצה מגניבה המכילה את C שווה לה.

נניח שקיים איבר שאין לו הפרש רציונאלי עם אף איבר בC. אזי אם נוסיף אותו לC נקבל קבוצה מגניבה המכילה ממש את C בסתירה.

תרגיל. הוכח שלכל מרחב וקטורי קיים בסיס

הוכחה. נביט באוסף הקבוצות הבלתי תלויות. קל להראות שלכל שרשרת באוסף זה יש חסם מלעיל: איחוד כל הקבוצות. אם האיחוד היה ת"ל סימן שהיו מספר סופי של וקטורים עם צ"ל לא טריוויאלי שמתאפס. כל אחד מהוקטורים האלה מוכל בקבוצה אחת בשרשרת, ומכיוון שזו שרשרת הקבוצה הכי גדולה מבינהן מכילה את כל הוקטורים. לכן הקבוצה הזו ת"ל בסתירה.

לכן יש קבוצה בת"ל מקסימלית, קל להוכיח שהיא פורשת ולכן מהווה בסיס.

מקור: https://math-wiki.com/index.php?title=88-195_בדידה_לתיכוניסטים_תשעא/מערך_שיעור/שיעור_8&oldid=25574