הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/תרגילים/תרגיל 3"

גרסה מ־12:23, 16 בנובמבר 2012

תוכן עניינים

1 שאלה 1
2 שאלה 2
3 שאלה 3
4 שאלה 4
5 שאלה 5

שאלה 1

יהי 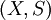$(X,S)$ מרחב מדיד, ותהי 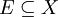$E \subseteq X$ . הוכיחו:

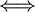$E$ מדידה $\iff$ פונקציית האינדיקטור 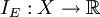$I_E:X \rightarrow \mathbb{R}$ היא מדידה.

שאלה 2

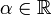בהגדרה של פונקציה מדידה, דרשנו שאחד מהתנאים $(i),(ii),(iii),(iv)$ יתקיים לכל $\alpha \in \mathbb{R}$ . הוכיחו שניתן להחליש את הדרישה באופן הבא:

אם  $E \subseteq \mathbb{R}$  תת קבוצה צפופה של  $\mathbb{R}$ , ולכל  $\alpha \in E$  אחד מהתנאים  $(i),(ii),(iii),(iv)$  מתקיימים, אזי הפונקציה מדידה.

שאלה 3

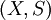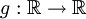יהיו $(X,S)$ מ"מ, $f:X \rightarrow \mathbb{R}$ מדידה, ו- $g:\mathbb{R} \rightarrow \mathbb{R}$ רציפה. הוכיחו כי הרכבת הפונקציות, 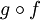$g \circ f$ היא פונקציה מדידה.

(הערה: תרגיל זה יכול להסביר למה הפונקציות $\sin(2x),\cos(x)+1$ מהתרגול הן מדידות).

שאלה 4

תהי 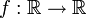$f:\mathbb{R} \rightarrow \mathbb{R}$ מדידה בורל. הוכיחו כי הקבוצות הבאות מדידות בורל (העזרו בשאלה הקודמת):

א. 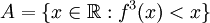$A=\{ x \in \mathbb{R}:f^3(x)<x \}$

ב. 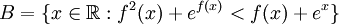$B=\{x \in \mathbb{R}: f^2(x)+e^{f(x)}<f(x)+e^x \}$

שאלה 5

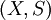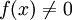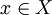יהי $(X,S)$ מ"מ. הוכיחו ישירות מההגדרה כי אם $f:X \rightarrow \mathbb{R}$ מדידה ומקיימת $f(x) \neq 0$ לכל $x \in X$ , אזי הפונקציה $\frac{1}{f} :X \rightarrow\mathbb{R}$ גם היא מדידה.

בהצלחה!

@@ שורה 10: / שורה 10: @@
 == שאלה 3 ==
-יהיו <math>(X,S)</math> מ"מ, <math>f:X \rightarrow \mathbb{R}</math> ו-<math>g:\mathbb{R} \rightarrow \mathbb{R}</math> רציפה. הוכיחו כי הרכבת הפונקציות, <math>g \circ f</math> היא פונקציה מדידה.
+יהיו <math>(X,S)</math> מ"מ, <math>f:X \rightarrow \mathbb{R}</math> מדידה, ו-<math>g:\mathbb{R} \rightarrow \mathbb{R}</math> רציפה. הוכיחו כי הרכבת הפונקציות, <math>g \circ f</math> היא פונקציה מדידה.
 ('''הערה:''' תרגיל זה יכול להסביר למה הפונקציות <math>\sin(2x),\cos(x)+1</math> מהתרגול הן מדידות).

הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/תרגילים/תרגיל 3"

גרסה מ־12:23, 16 בנובמבר 2012

תוכן עניינים

שאלה 1

שאלה 2

שאלה 3

שאלה 4

שאלה 5

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים