הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/הוכחה תקינה"
מתוך Math-Wiki
(יצירת דף עם התוכן "כזכור, עלינו להוכיח שלכל <math>n \in \mathbb{N}</math> ולכל <math>0<x<n</math> מתקיים כי <math>\left(1-\frac{x}{n+1} \right)^{n+1} \...") |
|||
| שורה 1: | שורה 1: | ||
כזכור, עלינו להוכיח שלכל <math>n \in \mathbb{N}</math> ולכל <math>0<x<n</math> מתקיים כי <math>\left(1-\frac{x}{n+1} \right)^{n+1} \ge \left( 1-\frac{x}{n} \right)^n</math> או <math>\left(1-\frac{x}{n+1} \right)^\frac{n+1}{n} \ge 1-\frac{x}{n}</math>. ע"פ אי שוויון ברנולי מתקיים: | כזכור, עלינו להוכיח שלכל <math>n \in \mathbb{N}</math> ולכל <math>0<x<n</math> מתקיים כי <math>\left(1-\frac{x}{n+1} \right)^{n+1} \ge \left( 1-\frac{x}{n} \right)^n</math> או <math>\left(1-\frac{x}{n+1} \right)^\frac{n+1}{n} \ge 1-\frac{x}{n}</math>. ע"פ אי שוויון ברנולי מתקיים: | ||
| − | <math>\left(1-\frac{x}{n+1} \right)^{n+1} \ge 1-\frac{x}{n+1} \frac{n+1}{n}</math> וזהו! | + | <math>\left(1-\frac{x}{n+1} \right)^\frac{n+1}{n} \ge 1-\frac{x}{n+1} \frac{n+1}{n}</math> וזהו! |
גרסה אחרונה מ־18:19, 22 בנובמבר 2012
כזכור, עלינו להוכיח שלכל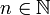 
ולכל 
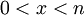מתקיים כי 
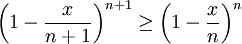או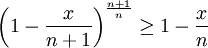 
. ע"פ אי שוויון ברנולי מתקיים:
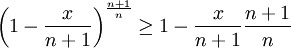וזהו!
