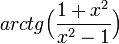הבדלים בין גרסאות בדף "Mathwiki:ארגז חול"
מתוך Math-Wiki
(←שאלה 4) |
(←שאלה 4) |
||
| שורה 31: | שורה 31: | ||
<math>\lim_{x\rightarrow \frac{\pi}{2}}arctg(xtg^2(x))=\frac{\pi}{2}</math> | <math>\lim_{x\rightarrow \frac{\pi}{2}}arctg(xtg^2(x))=\frac{\pi}{2}</math> | ||
| + | |||
| + | |||
| + | חשבו תחום חח"ע, תחום על, והופכית עבור <math>arctg\Big(\frac{1+x^2}{x^2-1}\Big)</math> | ||
==קישור== | ==קישור== | ||
[[file:flower.jpg|200px|link=http://www.math-wiki.com/index.php?title=%D7%A1%D7%A8%D7%98%D7%95%D7%A0%D7%99%D7%9D:%D7%9E%D7%AA%D7%9E%D7%98%D7%99%D7%A7%D7%94_%D7%91%D7%93%D7%99%D7%93%D7%94|alt= "הרצאות מצולמות בקורס מתמטיקה בדידה"|הרצאות מצולמות בקורס מתמטיקה בדידה]] | [[file:flower.jpg|200px|link=http://www.math-wiki.com/index.php?title=%D7%A1%D7%A8%D7%98%D7%95%D7%A0%D7%99%D7%9D:%D7%9E%D7%AA%D7%9E%D7%98%D7%99%D7%A7%D7%94_%D7%91%D7%93%D7%99%D7%93%D7%94|alt= "הרצאות מצולמות בקורס מתמטיקה בדידה"|הרצאות מצולמות בקורס מתמטיקה בדידה]] | ||
גרסה מ־18:44, 2 בינואר 2014
שאלה 1
הוכיחו לפי ההגדרה 
הוכיחו לפי ההגדרה 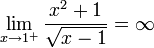
הוכיחו לפי ההגדרה 
שאלה 2
![f(x)=\frac{3}{1-\sqrt{x}}-\frac{2}{1-\sqrt[3]{x}}](/images/math/d/1/b/d1b795c7bef9fb9ca92c20556e305ac6.png)

חשבו את 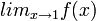
חשבו את 
חשבו את 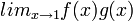
חשבו את 
שאלה 4
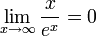
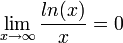
![\lim_{x\rightarrow\infty}\sqrt[x]{x}=1](/images/math/6/e/6/6e68396a1fca97ac1f3d224e67c25a80.png)
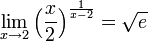
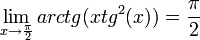
חשבו תחום חח"ע, תחום על, והופכית עבור