הבדלים בין גרסאות בדף "בדידה לתיכוניסטים תש"ע - שאלות ותשובות"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏תשובה)
(←‏תשובה)
שורה 30: שורה 30:
  
 
איך רפלקסיביות צריכה להראות במקרה הזה לדעתך?
 
איך רפלקסיביות צריכה להראות במקרה הזה לדעתך?
 +
 +
הבנתי:
 +
לכל <math>(a,b)\in (A\times B)</math>
 +
 +
 +
<math> ((a,b),(a,b))\in G </math>
 +
 +
תודה.
  
 
==הערה==
 
==הערה==

גרסה מ־23:06, 29 ביולי 2010

{n \choose k} = {n!\over k!(n-k)!}

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - תרגיל 1

שאלות

תרגיל 6

בתרגיל מבקשים להוכיח יחס שקילות של AxB. ע"פ ההגדרה שרשומה לי במחברת: R יחס על A נקרא ריפלקסיבי אם לכל a ששיך ל-A (a,a שייך ל R.

ההגדרה לא מציינת כיצד יחס שמעל 2 קבוצות שונות יכול לקיים ריפלקסיביות. אז איך אפשר להוכיח שAxB שקילות?


אדי

תשובה

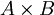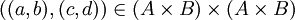
שים לב כי A\times B הינה קבוצה. והאיברים בG הם מהצורה ((a,b),(c,d))\in (A\times B) \times (A \times B)

איך רפלקסיביות צריכה להראות במקרה הזה לדעתך?

הבנתי: לכל 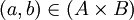(a,b)\in (A\times B)


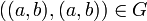
((a,b),(a,b))\in G 

תודה.

הערה

נא לא למחוק שאלות ותשובות. התשובות יכולות לסייע לאחרים.

תרגילים 3 ו4

בשאלה 3 א' ו-ב' צ"ל שאם האיחוד של כל הAi-ים שווה לA אז R רפלקסיבי (וב-ב' ההפך)? אבל העובדה שהאיחוד של כל הAi-ים שווה לA כבר נתונה בתחילת השאלה!

בשאלה 4, למשל בסעיף א', צריך להוכיח שאם R מוכל ב-V (שנתון שR שווה לV, מה ההגיון?) וS מוכל ב-W (שגם הם שווים) אז S הרכבה R מוכל ב W הרכבה V (שידוע לנו בכל מקרה שהם שווים?!).

תשובה

  • לא נתון בשאלה 3 שהאיחוד של תתי הקבוצות שווה לA, רק נתון שהן תתי קבוצות (יכולים להיות כולם שווים לקבוצה הריקה למשל)
  • איפה נתון שR שווה לV או S שווה לW? אני לא רואה את הנתון הזה. 'מוכל שווה' זה לא אותו דבר כמו 'שווה'.
נתון שR שווה לV, כי כתוב בתחילת השאלה ששניהם שווים ל AxB, וככה גם עם S וW.
אני מסתכל על התרגיל ורואה את הסימן 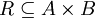R\subseteq A\times B ולא רואה את הסימן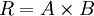 R= A\times B

הערה

אני בכל זאת חושב שיש טעות בשאלה 3 ג. מבקשים להוכיח ריפלקסיביות כתוצאה של זרות אבל ריפלקסיביות נובע מהאיחוד וטרנסטיביות היא שנובעת מחיתוך ריק של כל הקבוצות. [אדי גוטליב]

אדי, שים לב לשאלה הוכח/הפרך. כלומר, אתה צריך להוכיח אם זה נכון או להפריך במקרה ולדעתך זה לא נכון.
מכיוון שמשפט יכול להיות בלבד נכון או לא נכון, אי אפשר לעשות טעות בשאלת הוכח/הפרך :)
--ארז שיינר 15:38, 29 ביולי 2010 (IDT)

הבנתי :) = לא קראתי נכון את ההוראות.

תרגיל 2

בתרגיל שתיים יש שאלות עם הרכבה של שתי קבוצות ואנחנו למדנו רק על הרכבה של פונקציות...מה לעשות?

תשובה

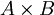שאלה טובה. זו לא "הרכבה של קבוצות". זו הרכבה של יחסים. בהגדרה, יחס בין A לB הוא תת-קבוצה של A \times B.

פונקציה היא בפרט יחס חד-ערכי.

הרכבת יחסים, בדומה להרכבת פונקציות, מוגדרת כדלקמן:

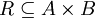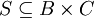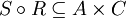
אם R \subseteq A \times B וגם S \subseteq B \times C אז S \circ R \subseteq A \times C

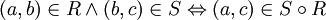כך ש(a,b) \in R \wedge (b,c) \in S \Leftrightarrow (a,c) \in S \circ R.

עמכם הסליחה על שההגדרה הזו לא הופיעה בקובץ. Adam Chapman 23:33, 28 ביולי 2010 (IDT)


תרגיל 2

שהעלתם את התרגיל השני, אבל לא כתבתם תאריך הגשה. מתי צריך להגיש אותו? תודה, שלומי



מקור: https://math-wiki.com/index.php?title=בדידה_לתיכוניסטים_תש%22ע_-_שאלות_ותשובות&oldid=3987