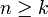הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5"
מתוך Math-Wiki
אחיה בר-און (שיחה | תרומות) |
אחיה בר-און (שיחה | תרומות) |
||
| שורה 9: | שורה 9: | ||
למה זה מספיק? | למה זה מספיק? | ||
| − | בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור <math>n=1</math> כלומר <math>P(1)</math> מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור <math>n=1</math> (שזה אכן כך) אז הטענה נכונה גם עבור <math>n=2</math>כלומר <math>P(2)</math>. אה! אז עכשיו זה נכון עבור <math>n=2</math> אז לפי אותה טענה זה נכון גם עבור <math>n=3</math>! ומה עכשיו? אם זה נכון עבור <math>n=3</math> זה נכון עבור <math>n=4</math> . אפשר להשתכנע | + | בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור <math>n=1</math> כלומר <math>P(1)</math> מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור <math>n=1</math> (שזה אכן כך) אז הטענה נכונה גם עבור <math>n=2</math>כלומר <math>P(2)</math>. אה! אז עכשיו זה נכון עבור <math>n=2</math> אז לפי אותה טענה זה נכון גם עבור <math>n=3</math>! ומה עכשיו? אם זה נכון עבור <math>n=3</math> זה נכון עבור <math>n=4</math> . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר <math>P(n)</math> נכון '''לכל''' <math>n</math> |
| + | |||
| + | ==הכללות== | ||
| + | ===הכללה פשוטה=== | ||
| + | הכללה ישירה מתבצעת כך (החלפה רק של הטענה הראשונה): אם נוכיח עבור טענה <math>P(n)</math> ש: | ||
| + | * הטענה מתקיימת עבור <math>n=k</math> מסוים כלומר <math>P(k)</math> מתקיים | ||
| + | * '''אם''' הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר <math>P(n)\Rightarrow P(n+1)</math>. | ||
| + | |||
| + | אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq k</math> | ||
| + | |||
| + | == הכללה מעמיקה == | ||
גרסה מ־08:31, 17 ביולי 2014
רעיון בסיסי - אינדוקציה על הטבעיים
בשביל להוכיח שטענה מסוימת 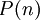 נכונה עבור כל מספר טבעי
(למשל
נכונה עבור כל מספר טבעי
(למשל 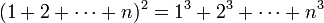 ) מספיק להוכיח את הבאים:
) מספיק להוכיח את הבאים:
- הטענה מתקיימת עבור
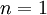 כלומר
כלומר 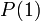 מתקיים
מתקיים - אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
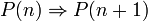 .
.
למה זה מספיק?
בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור 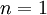 כלומר
כלומר 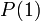 מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור
מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור 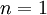 (שזה אכן כך) אז הטענה נכונה גם עבור
(שזה אכן כך) אז הטענה נכונה גם עבור 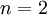 כלומר
כלומר 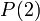 . אה! אז עכשיו זה נכון עבור
. אה! אז עכשיו זה נכון עבור 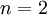 אז לפי אותה טענה זה נכון גם עבור
אז לפי אותה טענה זה נכון גם עבור 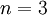 ! ומה עכשיו? אם זה נכון עבור
! ומה עכשיו? אם זה נכון עבור 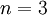 זה נכון עבור
זה נכון עבור 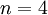 . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר
. וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר 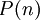 נכון לכל
נכון לכל 
הכללות
הכללה פשוטה
הכללה ישירה מתבצעת כך (החלפה רק של הטענה הראשונה): אם נוכיח עבור טענה 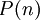 ש:
ש:
- הטענה מתקיימת עבור
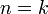 מסוים כלומר
מסוים כלומר 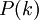 מתקיים
מתקיים - אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
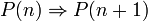 .
.
אז באופן דומה הטענה נכונה 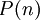 נכונה עבור
נכונה עבור