גרסה אחרונה מ־14:35, 2 ביולי 2015

תוכן עניינים

1 אינטגרל לפי רימן

אינטגרל לפי רימן

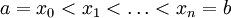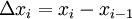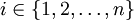הגדרה: יהי $[a,b]$ קטע סגור. נסמן את $T_{[a,b]}$ כחלוקה $a=x_0<x_1<\dots<x_n=b$ ונקרא ל-T חלוקה. נסמן $\Delta x_i=x_i-x_{i-1}$ כאשר $i\in\{1,2,\dots,n\}$ .

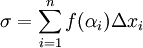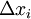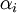הגדרה: תהי f פונקציה המוגדרת ב- $[a,b]$ ותהי T חלוקה של הקטע. עבור כל תת קטע $[x_{i-1},x_i]$ נבחר נקודה $\alpha_i\in[x_{i-1},x_i]$ ונבנה סכום מהצורה $\sigma=\sum_{i=1}^n f(\alpha_i)\Delta x_i$ . סכום זה נקרא סכום רימן של f והוא תלוי ב- $\Delta x_i$ וב- $\alpha_i$ .

הגדרה: פרמטר החלוקה של T מוגדר כ-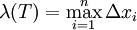 $\lambda(T)=\max_{i=1}^n\Delta x_i$ .

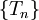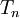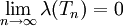הגדרה: תהי $\{T_n\}$ סדרת חלוקות של הקטע $[a,b]$ . נאמר כי $T_n$ נורמלית אם $\lim_{n\to\infty}\lambda(T_n)=0$ .

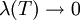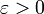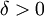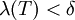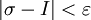הגדרה: נאמר כי סכומי רימן שואפים לגבול I כאשר $\lambda(T)\to0$ אם לכל $\varepsilon>0$ קיימת $\delta>0$ כך שלכל חלוקה T עבורה $\lambda(T)<\delta$ מתקיים $|\sigma-I|<\varepsilon$ .

דוגמה 1

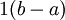נמצא פונקציה לא אינטגרבילית. דוגמה קלאסית לכך היא פונקצית דיריכלה - לכל חלוקה נורמלית שנבחר תהיה נקודה רציונלית ונקודה אי-רציונלית בתת קטע $[x_{i-1},x_i]$ של $[a,b]$ ולכן סכום רימן יכול להיות כל ערך בין 0 ל- $1(b-a)$ (כולל).

דוגמה 2

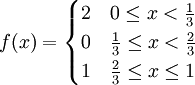קבע אינטגרביליות של f בקטע $[0,1]$ כאשר $f(x)=\begin{cases}2&0\le x<\tfrac13\\0&\tfrac13\le x<\tfrac23\\1&\tfrac23\le x\le1\end{cases}$ .

פתרון

נוכיח אינטגרביליות לפי רימן. תהי 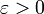$\varepsilon>0$ נתונה. צריך להוכיח כי קיימת 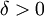$\delta>0$ כך שלכל חלוקה T, עבורה 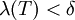$\lambda(T)<\delta$ מתקיים 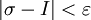$|\sigma-I|<\varepsilon$ . נצייר את הפונקציה:

גרף (1)

אינטואיטיבית, מהגרף ניתן לראות שהשטח מתחת ל-f הוא 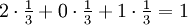$2\cdot\tfrac13+0\cdot\tfrac13+1\cdot\tfrac13=1$ , כלומר אנו ננסה להוכיח ש- $I=1$ :

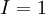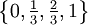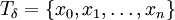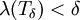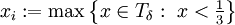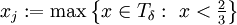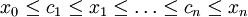נסמן ב-T את החלוקה $\left\{0,\tfrac13,\tfrac23,1\right\}$ של $[0,1]$ . נבחר $T_\delta=\{x_0,x_1,\dots,x_n\}$ העדנה של T המקיימת $\lambda(T_\delta)<\delta$ ונבנה את סכום רימן באופן הבא: תהי $x_i:=\max\left\{x\in T_\delta:\ x<\tfrac13\right\}$ ותהי $x_j:=\max\left\{x\in T_\delta:\ x<\tfrac23\right\}$ . עבור $x_0\le c_1\le x_1\le\dots\le c_n\le x_n$ , סכומי רימן הם

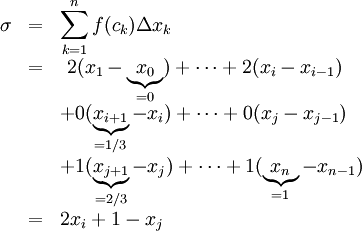
\begin{array}{l l l}\sigma&=&\displaystyle\sum_{k=1}^n f(c_k)\Delta x_k \\&=&\ 2(x_1-\underbrace{x_0}_{=0})+\dots+2(x_i-x_{i-1}) \\&&+0(\underbrace{x_{i+1}}_{=1/3}-x_i)+\dots+0(x_j-x_{j-1}) \\&&+1(\underbrace{x_{j+1}}_{=2/3}-x_j)+\dots+1(\underbrace{x_n}_{=1}-x_{n-1})\\&=&2x_i+1-x_j\end{array}

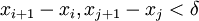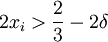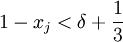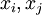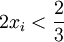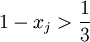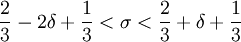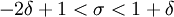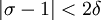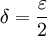נשים לב כי $x_{i+1}-x_i,x_{j+1}-x_j<\delta$ ולכן $2x_i>\frac23-2\delta$ ו- $1-x_j<\delta+\frac13$ . כמו כן, לפי הגדרת $x_i,x_j$ , מתקיים $2x_i<\frac23$ ו- $1-x_j>\frac13$ . מכאן ש- $\frac23-2\delta+\frac13<\sigma<\frac23+\delta+\frac13$ . נזכיר כי חשדנו ש- $I=1$ ולכן נבדוק מהו $\sigma-1$ : $-2\delta+1<\sigma<1+\delta$ ולכן $|\sigma-1|<2\delta$ . נבחר $\delta=\frac\varepsilon2$ ונקבל את הדרוש. לסיכום, ערך האינטגרל הוא 1 ובוודאי ש-f אינטגרבילית. $\blacksquare$

דוגמה 3

חשב את הגבול $\lim_{n\to\infty}\sqrt[n]{\left(1+\frac1n\right)\left(1+\frac2n\right)\dots\left(1+\frac nn\right)}$ .

פתרון

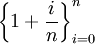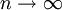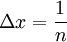נתבונן בסדרה $\left\{1+\frac in\right\}_{i=0}^n$ . כאשר $n\to\infty$ , קל לראות שמדובר בקטע $[1,2]$ . לפי חוקי לוגריתמים אפשר לרשום: $\lim_{n\to\infty} \ln\sqrt[n]{\prod_{i=1}^n\left(1+\frac in\right)}=\lim_{n\to\infty} \frac1n \ln \prod_{i=1}^n\left(1+\frac in\right)=\lim_{n\to\infty}\frac1n \sum_{i=1}^n\ln\left(1+\frac in\right)$ . 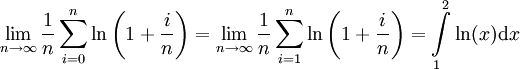ברור כי ln אינטגרבילית ב- $(1,2]$ ולכן נבחר חלוקה שעבורה $\Delta x=\frac1n$ , ואז $\lim_{n\to\infty}\frac1n \sum_{i=0}^n \ln\left(1+\frac in\right)=\lim_{n\to\infty}\frac1n \sum_{i=1}^n \ln\left(1+\frac in\right)=\int\limits_1^2\ln(x)\mathrm dx$ .

הערה: את האינטגרל הזה נלמד לפתור בשיעור הבא.

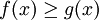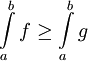משפט: אם $f(x)\ge g(x)$ ו-f ו-g אינטגרביליות אז $\int\limits_a^b f\ge\int\limits_a^b g$ .

דוגמה 4

קבע האם האינטגרל הנתון בעל ערך חיובי או שלילי: 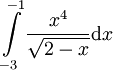$\int\limits_{-3}^{-1}\frac{x^4}{\sqrt{2-x}}\mathrm dx$ .

פתרון

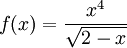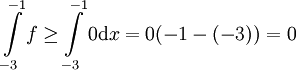נסמן $f(x)=\frac{x^4}{\sqrt{2-x}}$ קל לראות ש-f חיובית בקטע $[-3,-1]$ ולכן $\int\limits_{-3}^{-1}f\ge\int\limits_{-3}^{-1} 0\mathrm dx=0(-1-(-3))=0$ , כלומר אי-שלילי. נעיר ש- 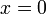$x=0$ (שהיא הנקודה המאפסת היחידה של f ב- 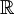$\mathbb R$ ) אינה בקטע ולכן התוצאה חיובית. $\blacksquare$

דוגמה 5

נוכיח כי 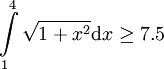$\int\limits_1^4\sqrt{1+x^2}\mathrm dx\ge7.5$ .

פתרון

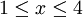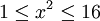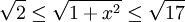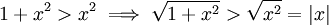נתון כי $1\le x\le4$ ולכן $1\le x^2\le16$ . מכאן ש- $\sqrt2\le\sqrt{1+x^2}\le\sqrt{17}$ חיובית. נפעיל אינטגרל (צריכים רק את צד שמאל) ונקבל $\int\limits_1^4 f\ge\int\limits_1^4\sqrt2\mathrm dx=\left[\sqrt2x\right]_{x=1}^4=\sqrt2\cdot4-\sqrt2=3\sqrt2$ . התוצאה קטנה מ-7.5 ולכן נחפש חסם אחר: $1+x^2>x^2\implies\sqrt{1+x^2}>\sqrt{x^2}=|x|$ , לכן $\int\limits_1^4 f>\int\limits_1^4|x|\mathrm dx=\int\limits_1^4 x\mathrm dx=\left[\frac{x^2}2\right]_{x=1}^4=7.5$ . $\blacksquare$

דוגמה 6

הוכח כי $\frac2{\sqrt[4]e}\le\int\limits_0^2 e^{x^2-x}\mathrm dx\le2e^2$

פתרון

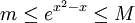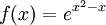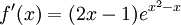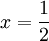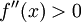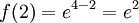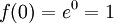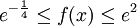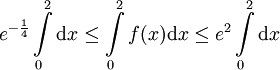ננסה למצוא קבועים המקיימים $m\le e^{x^2-x}\le M$ (כי אינטגרל של קבוע אנו יודעים לפתור). נמצא מינימום ומקסימום. נסמן $f(x)=e^{x^2-x}$ ואז $f'(x)=(2x-1)e^{x^2-x}$ ולכן נקודה החשודה כקיצון היא $x=\frac12$ : $f''(x)>0$ ולפיכך היא מינימום. לפי וירשטרס נחפש גם בקצוות: $f(2)=e^{4-2}=e^2$ (מקסימום) וכן $f(0)=e^0=1$ . לכן $e^{-\frac14}\le f(x)\le e^2$ . לפיכך $e^{-\frac14}\int\limits_0^2\mathrm dx\le \int\limits_0^2 f(x)\mathrm dx\le e^2\int\limits_0^2\mathrm dx$ ונקבל בדיוק את מה שרשום. $\blacksquare$

@@ שורה 34: / שורה 34: @@
 ==דוגמה 3==
-חשב את הגבול <math>\lim{n\to\infty}\sqrt[n]{\left(1+\frac1n\right)\left(1+\frac2n\right)\dots\left(1+\frac nn\right)}</math>.
+חשב את הגבול <math>\lim_{n\to\infty}\sqrt[n]{\left(1+\frac1n\right)\left(1+\frac2n\right)\dots\left(1+\frac nn\right)}</math>.
 ===פתרון===
 נתבונן בסדרה <math>\left\{1+\frac in\right\}_{i=0}^n</math>. כאשר <math>n\to\infty</math>, קל לראות שמדובר בקטע <math>[1,2]</math>. לפי חוקי לוגריתמים אפשר לרשום: <math>\lim_{n\to\infty} \ln\sqrt[n]{\prod_{i=1}^n\left(1+\frac in\right)}=\lim_{n\to\infty} \frac1n \ln \prod_{i=1}^n\left(1+\frac in\right)=\lim_{n\to\infty}\frac1n \sum_{i=1}^n\ln\left(1+\frac in\right)</math>. ברור כי ln אינטגרבילית ב-<math>(1,2]</math> ולכן נבחר חלוקה שעבורה <math>\Delta x=\frac1n</math>, ואז <math>\lim_{n\to\infty}\frac1n \sum_{i=0}^n \ln\left(1+\frac in\right)=\lim_{n\to\infty}\frac1n \sum_{i=1}^n \ln\left(1+\frac in\right)=\int\limits_1^2\ln(x)\mathrm dx</math>.

הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/27.2.11"

גרסה אחרונה מ־14:35, 2 ביולי 2015

תוכן עניינים

אינטגרל לפי רימן

דוגמה 1

דוגמה 2

פתרון

דוגמה 3

פתרון

דוגמה 4

פתרון

דוגמה 5

פתרון

דוגמה 6

פתרון

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים