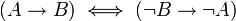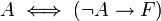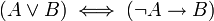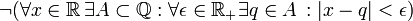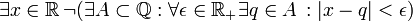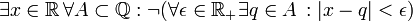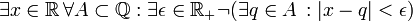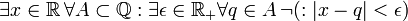הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 0"
אחיה בר-און (שיחה | תרומות) (←קשרים) |
אחיה בר-און (שיחה | תרומות) |
||
| שורה 4: | שורה 4: | ||
סיכום הנושא המלא נמצא בדף [[88-101 חשיבה מתמטית]]. | סיכום הנושא המלא נמצא בדף [[88-101 חשיבה מתמטית]]. | ||
| − | == | + | ==פסוקים וקַשָּרִים, פרדיקטים וכַּמָּתִים, הצרנה וטבלאות אמת== |
| − | === אטומים | + | === אטומים, פסוקים וקשרים=== |
הגדרה (לא פורמאלית): השפה העברית מורכבת ממשפטים. המקבילה בשפה המתמטית נקראת "פסוק".ה'''אטומים''' הם חלק מאבני היסוד של הפסוקים. | הגדרה (לא פורמאלית): השפה העברית מורכבת ממשפטים. המקבילה בשפה המתמטית נקראת "פסוק".ה'''אטומים''' הם חלק מאבני היסוד של הפסוקים. | ||
לדוגמא: הפסוק "שנת הלימודים החלה ויש 5 קורסים בשנה א'" מורכב משני אטומים- "שנת הלימודים החלה" ו"יש 5 קורסים בשנה א'" (שני האטומים מקשורים ע"י וו החיבור) | לדוגמא: הפסוק "שנת הלימודים החלה ויש 5 קורסים בשנה א'" מורכב משני אטומים- "שנת הלימודים החלה" ו"יש 5 קורסים בשנה א'" (שני האטומים מקשורים ע"י וו החיבור) | ||
| − | + | בצורה אחרת: אטומים הם יחידה תוכן בסיסית. פסוקים הם יחידות יותר מורכבות המורכבות מאטומים וקשרים. אטום מקבל ערך אמת TRUE ׁויסומן ב T או 1 (כלומר הוא אמיתי) או ערך עמת FULSE ויסומן ב F או 0 ׁ(כלומר הוא שקרי). פסוקים יקבלו ערך אמת לפי ערכי האמת של האטומים והקשרים המעורבים בפסוק. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | כפי שציינו פסוקים הם יחידות תוכן יותר מורכבות בשל השימוש בקשרים. |
| − | + | ==== קשרים ==== | |
| − | הגדרה: יהיו A,B אטומים (או | + | הגדרה: יהיו A,B אטומים (או פסןקים) היכולים להיות אמת (1) או שקר (0) אזי הקשרים |
* <math>A\to B</math> - "גרירה" (חד כיוונית) | * <math>A\to B</math> - "גרירה" (חד כיוונית) | ||
* <math>A \or B</math> "או" | * <math>A \or B</math> "או" | ||
* <math>A\and B</math> "וגם" | * <math>A\and B</math> "וגם" | ||
* <math>\neg A</math> "שלילה" | * <math>\neg A</math> "שלילה" | ||
| − | מוגדרים ע"י טבלאת האמת הבאה: | + | מוגדרים ע"י טבלאת האמת הבאה (טבלת שכל שורה בה מתאימה להצבה אחרת אחרת באטומים): |
{| border="1" align="center" style="text-align:center;" | {| border="1" align="center" style="text-align:center;" | ||
| שורה 77: | שורה 72: | ||
* מספר (טבעי) מסוים n ניתן להצגה בעזרת 2 ספרות (בבסיס עשרוני) <math>\iff</math> המספר n קטן מ 100. הפסוק יקבל ערך T רק אם שני התנאים יתקיימו ביחד. במילים אחרות, אם אחד מתקיים גם השני. במילים אחרות, אם אחד לא מתקיים והשני אז השני גם לא מתקיים. | * מספר (טבעי) מסוים n ניתן להצגה בעזרת 2 ספרות (בבסיס עשרוני) <math>\iff</math> המספר n קטן מ 100. הפסוק יקבל ערך T רק אם שני התנאים יתקיימו ביחד. במילים אחרות, אם אחד מתקיים גם השני. במילים אחרות, אם אחד לא מתקיים והשני אז השני גם לא מתקיים. | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
תכונות הקשרים: | תכונות הקשרים: | ||
| שורה 88: | שורה 80: | ||
* כללי דה מורגן <math>\neg (A \lor B) = \neg A \land \neg B, \neg (A \land B) = \neg A \lor \neg B</math>. תוכיחו אחד מהם בתרגיל הבית | * כללי דה מורגן <math>\neg (A \lor B) = \neg A \land \neg B, \neg (A \land B) = \neg A \lor \neg B</math>. תוכיחו אחד מהם בתרגיל הבית | ||
| − | |||
| − | |||
| − | + | ==== הצרנה ==== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | === הצרנה === | + | |
הצרנה- כתיבת רעיון בעזרת ניסוח פורמאלי | הצרנה- כתיבת רעיון בעזרת ניסוח פורמאלי | ||
| שורה 118: | שורה 100: | ||
פתרון: נסמן A אני עייף, B אני רעב, C אני עצבני, D אני הולך לישון | פתרון: נסמן A אני עייף, B אני רעב, C אני עצבני, D אני הולך לישון | ||
ההצרנה <math>[(A\land B)\to (C\lor D)]\and[(C \land \lnot A)\to B]</math> | ההצרנה <math>[(A\land B)\to (C\lor D)]\and[(C \land \lnot A)\to B]</math> | ||
| + | |||
| + | ===פרדיקטים וכמתים=== | ||
| + | בניגוד לאטומים שהם ללא משתנים ה'''פרדיקטים''' הינם פונקציות התלויות במשתנים. לדוגמא ניתן להגדיר את הפרדיקט <math>S(x)</math> להיות x הינו סטודנט באוניברסיטה. | ||
| + | |||
| + | כיוון שאטומים הם ללא משתנים הם יכולים להיות T או F אבל לא שניהם. לעומתם פרדיקטים הם תלויים במשתנים ולכן ערך האמת שלהם יקבע לפי ההצבה במשתנים. למשל הפרדיקט <math>S(x,y)=x<y</math> יהיה נכון במקרה ש <math>S(2,3)</math> ולא נכון במקרה ש <math>S(3,2)</math>. כלומר לכל הצבה במשתני הפרדיקטים נקבל פסוק. הערה: משמשים בקשרים גם בפרדיקטים למשל <math>S(x,y)</math> הפרדיקט המוגדר <math>x>0 \land x<y</math> | ||
| + | |||
| + | |||
| + | בנוסף, ניתן להוסיף כמתים. | ||
| + | |||
| + | הכמת "לכל" <math>\forall</math> והכמת "קיים" <math>\exist</math> | ||
| + | |||
| + | תפקיד מרכזי של הכמת הוא להבהיר את כוונת הטענה. למשל הטענה ש "סטונדט הוא יצור חרוץ" יכולה לקבל 2 משמעויות בעזרת הכמתים. או "כל סטודנט הוא יצור חרוץ" או "קיים סטודנט שהוא יצור חרוץ". | ||
| + | |||
| + | הטענה הראשונה טוענת לגבי כלל הסטודנטים (אם רוצים להוכיח כי הטענה נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם חרוצים ואם רוצים להוכיח כי הטענה לא נכונה מספיק למצוא סטודנט אחד שאינו חרוץ). | ||
| + | |||
| + | לעומתה הטענה השניה טוענת שניתן למצוא סטודנט אחד (לפחות) שהוא חרוץ (אם רוצים להוכיח את הטענה צריך למצוא סטודנט שהוא חרוץ ואם רוצים להוכיח כי הטענה לא נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם אינם חרוצים | ||
| + | |||
הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים). | הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים). | ||
| שורה 125: | שורה 124: | ||
* <math>P(x)</math> הוא הפרדיקט "x" הוא ראשוני. | * <math>P(x)</math> הוא הפרדיקט "x" הוא ראשוני. | ||
* <math>Q(x)</math> הוא הפרדיקט <math>\forall a,b : p|ab \Rightarrow (p|a \lor p|b)</math> | * <math>Q(x)</math> הוא הפרדיקט <math>\forall a,b : p|ab \Rightarrow (p|a \lor p|b)</math> | ||
| + | |||
| + | הערה: אחרי שמכמתים על כל משתני הפרדיקט מקבלים פסוק ללא משתנים. | ||
| + | |||
| + | נשים לב כי בשביל לקבוע אם הפסוק <math>\forall x P(x)</math> אנחנו צריכים לדעת איזה x ים "חוקיים" (בהנחה שאנחנו יודעים את P) ומכאן שנעבור להגדרות הבאות. | ||
===הגדרות הקשורות לקבוצות=== | ===הגדרות הקשורות לקבוצות=== | ||
| שורה 176: | שורה 179: | ||
* <math>\ (A \leftrightarrow B) \equiv (A \rightarrow B) \wedge (B \rightarrow A)</math>. | * <math>\ (A \leftrightarrow B) \equiv (A \rightarrow B) \wedge (B \rightarrow A)</math>. | ||
* <math>\ (A \rightarrow B) \equiv ((\neg B) \rightarrow (\neg A))</math>. | * <math>\ (A \rightarrow B) \equiv ((\neg B) \rightarrow (\neg A))</math>. | ||
| + | |||
| + | הערה (טרמינולוגיה): | ||
| + | *כאשר אומרים ש B הוא תנאי הכרחי ל A פירושו הוא <math>A \to B</math> | ||
| + | *כאשר אומרים ש B הוא תנאי מספיק ל A פירושו הוא <math>B \to A</math> | ||
| + | *כאשר אומרים ש B הוא תנאי הכרחי ומספיק ל A פירושו הוא <math>B \iff A</math> | ||
דוגמאות מילוליות: | דוגמאות מילוליות: | ||
גרסה מ־15:19, 7 באוגוסט 2017
סיכום הנושא המלא נמצא בדף 88-101 חשיבה מתמטית.
תוכן עניינים
פסוקים וקַשָּרִים, פרדיקטים וכַּמָּתִים, הצרנה וטבלאות אמת
אטומים, פסוקים וקשרים
הגדרה (לא פורמאלית): השפה העברית מורכבת ממשפטים. המקבילה בשפה המתמטית נקראת "פסוק".האטומים הם חלק מאבני היסוד של הפסוקים. לדוגמא: הפסוק "שנת הלימודים החלה ויש 5 קורסים בשנה א'" מורכב משני אטומים- "שנת הלימודים החלה" ו"יש 5 קורסים בשנה א'" (שני האטומים מקשורים ע"י וו החיבור)
בצורה אחרת: אטומים הם יחידה תוכן בסיסית. פסוקים הם יחידות יותר מורכבות המורכבות מאטומים וקשרים. אטום מקבל ערך אמת TRUE ׁויסומן ב T או 1 (כלומר הוא אמיתי) או ערך עמת FULSE ויסומן ב F או 0 ׁ(כלומר הוא שקרי). פסוקים יקבלו ערך אמת לפי ערכי האמת של האטומים והקשרים המעורבים בפסוק.
כפי שציינו פסוקים הם יחידות תוכן יותר מורכבות בשל השימוש בקשרים.
קשרים
הגדרה: יהיו A,B אטומים (או פסןקים) היכולים להיות אמת (1) או שקר (0) אזי הקשרים
-
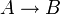 - "גרירה" (חד כיוונית)
- "גרירה" (חד כיוונית) -
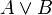 "או"
"או" -
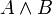 "וגם"
"וגם" -
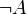 "שלילה"
"שלילה"
מוגדרים ע"י טבלאת האמת הבאה (טבלת שכל שורה בה מתאימה להצבה אחרת אחרת באטומים):
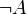
|
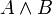
|
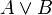
|
|

|

|
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
הערה: קשר נוסף שהינו נפוץ בתחום המתמטקיה והוא גרירה דו-כיוונית (ידוע בכינויו אם ורק אם, אמ"מ).
הגדרתו פשוטה (נובעת משמו..) והיא מוגדרת ע"י קשר הגרירה החד כיווני.
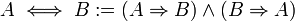
דוגמאות מילוליות:
- אם נסיים את החומר של השיעור אז נגמור מוקדם. אם נסיים את החומר וגם לא נגמור מוקדם אז הפסוק יקבל ערך F. אם לא נסיים את החומר וגם לא נגמור מוקדם אז הפסוק יקבל ערך T.
- אינדוקציה לומדים בתיכון וגם זה קל. הפסוק יקבל ערך T רק אם האטומים המרכיבים אותו יקבלו ערך T (כלומר שניהם יתקיימו)
- 3 הוא מספר ראשוני או 5 הוא מספר ראשוני. הפסוק הזה מקבל ערך T כיוון ש 3/5 מספר ראשוני. גם הפסוק "3 הוא מספר ראשוני או 4 הוא מספר ראשוני" הוא בעל ערך T.
- מספר (טבעי) מסוים n ניתן להצגה בעזרת 2 ספרות (בבסיס עשרוני)
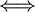 המספר n קטן מ 100. הפסוק יקבל ערך T רק אם שני התנאים יתקיימו ביחד. במילים אחרות, אם אחד מתקיים גם השני. במילים אחרות, אם אחד לא מתקיים והשני אז השני גם לא מתקיים.
המספר n קטן מ 100. הפסוק יקבל ערך T רק אם שני התנאים יתקיימו ביחד. במילים אחרות, אם אחד מתקיים גם השני. במילים אחרות, אם אחד לא מתקיים והשני אז השני גם לא מתקיים.
תכונות הקשרים:
- קיבוציות
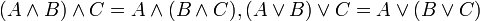
- חילופיות
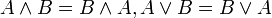
- פילוג
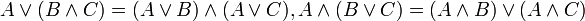
- כללי דה מורגן
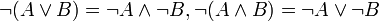 . תוכיחו אחד מהם בתרגיל הבית
. תוכיחו אחד מהם בתרגיל הבית
הצרנה
הצרנה- כתיבת רעיון בעזרת ניסוח פורמאלי
דוגמא: נצרין את המשפט: "אם יש בגרות בשעה חופפת לקורס אז הוא מתבטל ". נגדיר  = יש בגרות בשעה שחופפת לקורס.
= יש בגרות בשעה שחופפת לקורס.  = הקורס מתבטל. המשפט אומר
= הקורס מתבטל. המשפט אומר 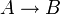 . כלומר בגרות בשעה חופפת לקורס זה תנאי מספיק לכך שהקורס מתבטל. שימו לב שזהו לא תנאי הכרחי כי יתכן שהקורס יתבטל מסיבות אחרות.
. כלומר בגרות בשעה חופפת לקורס זה תנאי מספיק לכך שהקורס מתבטל. שימו לב שזהו לא תנאי הכרחי כי יתכן שהקורס יתבטל מסיבות אחרות.
הצרן: למדתי היטב למבחן, ואף על פי כן נכשלתי בו.
פתרון: נסמן A למדתי לבמחן, B נכשלתי במבחן אזי ההצרנה היא 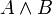
הצרן: "ערן לובש חולצה סגולה בכל פעם שהוא לובש מכנסיים בצבע שחור"
פתרון: נסמן A ערן לובש חולצה סגולה. נסמן B ערך לובש מכנסיים שחורות.
ההצרנה 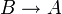
הצרן: "כאשר אני עייף ורעב אני נעשה עצבני, או שאני הולך לישון; אבל אם אני עצבני ולא עייף, אז אני רעב".
פתרון: נסמן A אני עייף, B אני רעב, C אני עצבני, D אני הולך לישון
ההצרנה ![[(A\land B)\to (C\lor D)]\and[(C \land \lnot A)\to B]](/images/math/6/f/b/6fb55523ae97afaffc04063f3e05da17.png)
פרדיקטים וכמתים
בניגוד לאטומים שהם ללא משתנים הפרדיקטים הינם פונקציות התלויות במשתנים. לדוגמא ניתן להגדיר את הפרדיקט 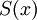 להיות x הינו סטודנט באוניברסיטה.
להיות x הינו סטודנט באוניברסיטה.
כיוון שאטומים הם ללא משתנים הם יכולים להיות T או F אבל לא שניהם. לעומתם פרדיקטים הם תלויים במשתנים ולכן ערך האמת שלהם יקבע לפי ההצבה במשתנים. למשל הפרדיקט 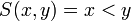 יהיה נכון במקרה ש
יהיה נכון במקרה ש 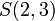 ולא נכון במקרה ש
ולא נכון במקרה ש 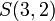 . כלומר לכל הצבה במשתני הפרדיקטים נקבל פסוק. הערה: משמשים בקשרים גם בפרדיקטים למשל
. כלומר לכל הצבה במשתני הפרדיקטים נקבל פסוק. הערה: משמשים בקשרים גם בפרדיקטים למשל 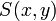 הפרדיקט המוגדר
הפרדיקט המוגדר 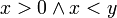
בנוסף, ניתן להוסיף כמתים.
הכמת "לכל" 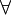 והכמת "קיים"
והכמת "קיים" 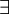
תפקיד מרכזי של הכמת הוא להבהיר את כוונת הטענה. למשל הטענה ש "סטונדט הוא יצור חרוץ" יכולה לקבל 2 משמעויות בעזרת הכמתים. או "כל סטודנט הוא יצור חרוץ" או "קיים סטודנט שהוא יצור חרוץ".
הטענה הראשונה טוענת לגבי כלל הסטודנטים (אם רוצים להוכיח כי הטענה נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם חרוצים ואם רוצים להוכיח כי הטענה לא נכונה מספיק למצוא סטודנט אחד שאינו חרוץ).
לעומתה הטענה השניה טוענת שניתן למצוא סטודנט אחד (לפחות) שהוא חרוץ (אם רוצים להוכיח את הטענה צריך למצוא סטודנט שהוא חרוץ ואם רוצים להוכיח כי הטענה לא נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם אינם חרוצים
הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים).
פתרון:
ההצרנה 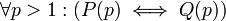 כאשר
כאשר
-
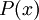 הוא הפרדיקט "x" הוא ראשוני.
הוא הפרדיקט "x" הוא ראשוני. -
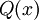 הוא הפרדיקט
הוא הפרדיקט 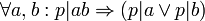
הערה: אחרי שמכמתים על כל משתני הפרדיקט מקבלים פסוק ללא משתנים.
נשים לב כי בשביל לקבוע אם הפסוק 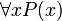 אנחנו צריכים לדעת איזה x ים "חוקיים" (בהנחה שאנחנו יודעים את P) ומכאן שנעבור להגדרות הבאות.
אנחנו צריכים לדעת איזה x ים "חוקיים" (בהנחה שאנחנו יודעים את P) ומכאן שנעבור להגדרות הבאות.
הגדרות הקשורות לקבוצות
ההגדרה האינטואיטיבית לקבוצה הינה "אוסף של איברים". בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות (קבוצות נוהגים לסמן בין 2 סוגריים מסולסלות):
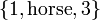 ,
, 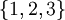 ו
ו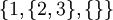
איבר השייך לקבוצה אנו מסמנים בסימן 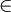 . למשל
. למשל 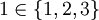 , ואילו
, ואילו 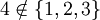 . שימו לב שגם
. שימו לב שגם 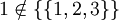 שכן האיבר היחיד בקבוצה זו הינה הקבוצה
שכן האיבר היחיד בקבוצה זו הינה הקבוצה 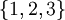 .
.
- אומרים שקבוצה A מוכלת בקבוצה B (מסומן
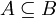 ) אם כל האיברים בA הם גם איברים בB.
) אם כל האיברים בA הם גם איברים בB.
- חיתוך של שתי קבוצות A ו B הינו אוסף האיברים השייכים גם לA וגם לB (מסומן
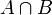 ).
). - איחוד של שתי קבוצות A ו B הינו אוסף האיברים השייכים לA או לB (מסומן
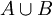 ).
). - A הפרש B הינה הקבוצה המכילה את כל האיברים בA שאינם בB (מסומן A\B).
- ההפרש הסימטרי בין שתי קבוצות A וB הוא אוסף האיברים הנמצאים באחת הקבוצות אך לא בחיתוך (מסומן
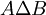 ).
).
תרגיל:
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
פתרון 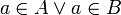
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
הגדרה: קבוצה A מוכלת בקבוצה B אם בB נמצאים כל האיברים מA (למשל הטבעיים מוכלים בשלמים 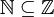 , והשלמים מוכלים בממשיים
, והשלמים מוכלים בממשיים 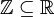 ).
).
- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
פתרון: ![\forall c [c\in C \rightarrow (c\in A \and c \in B)]](/images/math/4/9/e/49edfe222503e5df099cd89197852617.png)
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
טאוטולוגיות
הגדרה : טאוטולוגיה הינה ביטוי שנכון תמיד ללא תלות בערכים שמציבים בו.
למשל 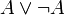
הגדרה: נאמר שביטוי  שקול טאוטולוגית לביטוי
שקול טאוטולוגית לביטוי  (ונסמן
(ונסמן 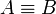 )
אם הביטוי
)
אם הביטוי 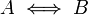 הינו טאוטולוגיה (במילים: A קורה אמ"מ B קורה)
הינו טאוטולוגיה (במילים: A קורה אמ"מ B קורה)
תרגיל: הוכח באמצעות טבלאות אמת שניתן להציג את הקשרים 'גרירה' ו'וגם' באמצעות 'או' ושלילה בלבד
פתרון:
מתקיים 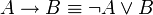 ומתקיים
ומתקיים 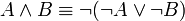
הוכח את הבאים:
-
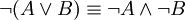
-
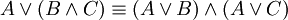
-
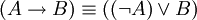 .
. -
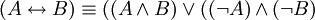 .
. -
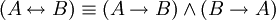 .
. -
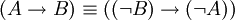 .
.
הערה (טרמינולוגיה):
- כאשר אומרים ש B הוא תנאי הכרחי ל A פירושו הוא
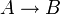
- כאשר אומרים ש B הוא תנאי מספיק ל A פירושו הוא
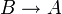
- כאשר אומרים ש B הוא תנאי הכרחי ומספיק ל A פירושו הוא
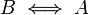
דוגמאות מילוליות:
- "כלב נובח אינו נושך" אם"ם "כלב נושך אינו נובח"
הסבר: נסמן ב- D את קבוצת כל הכלבים ב -A את הנובחים וב- B את הנושכים אז הדוגמא היא בעצם 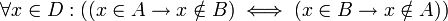
שזה בעצם מהצורה (לכל כלב) * 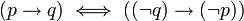 .
.
- מי שלא לומד בסמסטר נכשל במבחן אמ"מ מי שלא נכשל במבחן למד בסמסטר
דרכי הוכחה
הוכח שהפסוקים הבאים הינם טאוטולוגיות:
(נהוג להחליף ביטויים מהצורה הזו בביטויים השקולים להם כי הם נוחים יותר להוכחה מידי פעם.)
דוגמאות מילוליות:
- בשביל להוכיח את הטענה ש "אם מישהו יכתוב בדיחה במבחן במקום תשובה אז הוא יקבל ניקוד חלקי" ניתן להוכיח באופן שקול כי " אם מישהו לא קיבל ניקוד חלקי במבחן אז זה אומר שהוא לא כתב בדיחה במבחן במקום תשובה"
- בשביל להוכיח את הטענה ש "הגובה שלי נמוך מ- 3 מטר" אפשר להוכיח באופן שקול כי הגובה שלי לפחות 3 מטר ולהגיע לסתירה. למשל הטיעון הבא: "אם הגובה שלי לפחות 3 מטר, אז הראש שלי היה נוגע בתקרה. כיוון שהוא לא נוגע בתקרה, זו סתירה ולכן איני בגובה 3 מטר"
שלילת פסוקים
מהי השלילה של הפסוק "לכל סיר יש מכסה המתאים לו", או "לכל מאכל, יש מישהו שמכין אותו טעים"?
בעת שלילה של פסוק לוגי, הכמתים 'לכל' ו'קיים' מתחלפים זה עם זה, והשלילה עוברת הלאה. את השלילה על הקשרים ניתן לבצע באמצעות טאוטולוגיות וטבלאות אמת.
לדוגמא:
- "לכל אדם בעולם קיים דג עם מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם"
השלילה היא:
- "קיים אדם כך שלא קיים דג עם מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם"
נמשיך:
- "קיים אדם שלכל דג בעולם לא נכון ש(יש לו מספר קשקשים כגיל האדם או שאורכו עשירית מאורך האדם)"
כלומר
- "קיים אדם שלכל דג בעולם יש מספר קשקשים שונה מגיל האדם וגם אורכו של הדג שונה מעשירית אורך האדם"
הערה: סדר הכמתים הוא חשוב (כמו בעברית) - לדוגמא: יש הבדל בין "לכל סיר קיים מכסה" לבין "קיים מכסה שמתאים לכל סיר".דוגמא: הצרן את המשפט "לכל מספר טבעי יש מספר טבעי הגדול ממנו" פתרון: 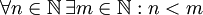 לעומת זאת
לעומת זאת 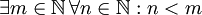 פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
- תרגיל: הצרן את המשפט "כל מספר ממשי ניתן לקרב ע"י מספרים רציונאליים בקירוב טוב כרצוננו"
פתרון: 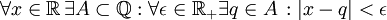 .
.
מה היא שלילתו של המשפט?
פתרון: נכתוב את הרמות השונות
תרגילים: דוגמאות של הצרנת ושלילת המושגים 'תלות לינארית', 'גבול סדרה', 'חח"ע', וכדומה
צורות נורמליות: CNF ,DNF
ישנן שתי "צורות נורמליות" להצגת כל פסוקית - DNF ו CNF.
DNF
ביטוי בצורת DNF מורכב מאוסף "פסוקיות" המחוברות ביניהן על ידי פעולות "או". כל פסוקית בעצמה מורכבת מאטומים המחוברים ביניהם על ידי פעולות "וגם". כל אטום הוא משתנה או שלילת משתנה.
בצורה סכמטית: 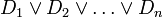 כאשר כל
כאשר כל 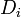 מהצורה
מהצורה 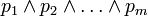 וכל
וכל 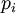 שווה למשתנה
שווה למשתנה  או לשלילתו
או לשלילתו 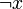 .
.
דוגמא: נמצא את צורת DNF של טבלת האמת הבאה:
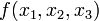
|
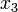
|
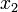
|
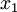
|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
נתמקד בשורות שערך האמת שלהן הוא 1 (שורות 3, 4, 6).
לשורה 3 נתאים את הפסוקית 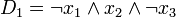
מה עשינו? החלפנו כל משתנה שערכו 0 בשלילה שלו, וכל משתנה שערכו 1 השארנו בלי לגעת.
מה יצא לנו מזה? שימו לב שרק הצבה של ערכי האמת של 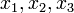 שמופיעים בשורה 3 תתן ערך אמת 1 ב
שמופיעים בשורה 3 תתן ערך אמת 1 ב 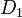 . כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 0 ב
. כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 0 ב 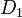 .
.
באופן דומה נייצר 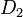 עבור שורה 4 ו
עבור שורה 4 ו 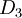 עבור שורה 6:
עבור שורה 6:
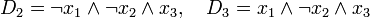
כעת ה DNF של טבלת האמת היא פשוט
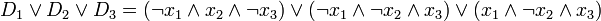 .
.
CNF
ביטוי בצורת CNF מורכב מאוסף "פסוקיות" המחוברות ביניהן על ידי פעולות "וגם". כל פסוקית בעצמה מורכבת מאטומים המחוברים ביניהם על ידי פעולות "או". כל אטום הוא משתנה או שלילת משתנה.
בצורה סכמטית: 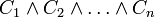 כאשר כל
כאשר כל 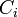 מהצורה
מהצורה
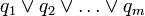 וכל
וכל 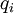 שווה למשתנה
שווה למשתנה  או לשלילתו
או לשלילתו 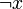 .
.
נדגים על הדוגמא לעיל.
נתמקד בשורות שערך האמת שלהן הוא 0 (שורות 1, 2, 5, 7, 8)
לשורה 1 נתאים את הפסוקית 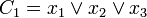
מה עשינו? כל משתנה שערכו 0 השארנו בלי לגעת, וכל משתנה שערכו 1 החלפנו בשלילתו.
מה יצא לנו מזה? שימו לב שרק הצבה של ערכי האמת של 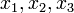 שמופיעים בשורה 1 תתן ערך אמת 0 ב
שמופיעים בשורה 1 תתן ערך אמת 0 ב 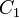 . כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 1 ב
. כל הצבה אחרת (כלומר: הצבה של ערכי אמת של המשתנים בשורה אחרת) תתן 1 ב 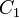 .
.
באופן דומה נייצר 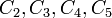 עבור שורות 2 , 5, 7 ו-8:
עבור שורות 2 , 5, 7 ו-8:
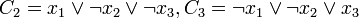
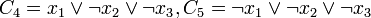
כעת ה CNF של טבלת האמת היא פשוט
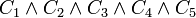
הרחבה על עניינים אלו ניתן למצוא פה 88-101 חשיבה מתמטית