הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏תרגיל 4 שאלה 2)
(←‏תרגיל 5 לבוחן?)
שורה 139: שורה 139:
  
 
::טוב, תודה. זה אותו הבוחן, לא?
 
::טוב, תודה. זה אותו הבוחן, לא?
 +
 +
:::לא יודע, תלוי אם הוא יכלול גם את מה שאתם למדתם על חתכי דדקינד וכל אלה (שאצל ד"ר הורוביץ הם לא נלמדו עדיין). אם כן - אז וודאי שהבחנים יהיהו שונים. אם לא - ייתכן שהם יהיו זהים. [[משתמש:Gordo6|גל א.]]

גרסה מ־20:17, 11 בנובמבר 2010

חזרה לדף הקורס


גלול לתחתית העמוד


הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

שאלות

בוחן לקבוצה של אפי

יש אפשרות שתגידו לנו מה יהיה סגנון השאלות בבוחן? לצטט משפטים? שאלות כמו בתרגילים?

נראה לי שאפי לא נכנס לפה, אבל אולי מישהו אחר יודע את סגנון השאלות?

שאלה כללית

אם לסדרה יש גבול חלקי אחד ויחיד ז"א שהסידרה מתכנסת לגבול זה?

בשאלה 2.b בתרגיל 4 אתם נדרשים להוכיח את זה --ארז שיינר 21:30, 8 בנובמבר 2010 (IST)
בהוכחה שלי לשאלה זאת הנחתי כמו ברמז שהגבול הוא משהו אחר ואז הגעתי לסתירה. אבל מה אם הגבול בכלל לא קיים?
מצב כזה יכול בכלל להתרחש?
אם כך, לא הוכחת את מה שהיה צריך להוכיח. כאשר רשום להוכיח שהגבול הינו L הכוונה שצריך להראות שיש גבול והוא L. מה שרשום שם אומר במפורש שאם הגבול החלקי העליון והתחתון שווים (זה בפרט המקרה של קיום גבול חלקי יחיד) אזי הסדרה מתכנסת לגבול הזה. --ארז שיינר 00:18, 9 בנובמבר 2010 (IST)

תיקון שאלה 4 תרגיל 5

על איזה תיקון בשאלה 4 תרגיל 5 אתה מדבר? בתרגיל עצמו לא מופיע תיקון...

לא רשום תיקון הוא פשוט מתוקן. היה בצד הימני n+1 במקום n-1, זה הכל. --ארז שיינר 14:46, 9 בנובמבר 2010 (IST)

בקשה לפתרון הבוחן

שלום רב,

אמנם הבוחן של הקבוצה של פרופסור זלצמן הוא ב-22/11 אבל לקבוצות של התיכוניסטים (ד"ר הורוביץ וד"ר שיין) יש בוחן ב-14/11. אני מאמין שאני מדבר בשמם של כל התיכוניסטים בבקשה להעלות את הפתרון לאתר עוד לפני הבוחן שלנו, זה מאוד יעזור לנו. תודה בכל מקרה! גל.

רוב השאלות ממילא הם משיעורי הבית. חוצמזה, זה בוחן ממש קל אני בטוח שתתמודדו. אם יש שאלה ספציפית מוזמנים לשאול. --ארז שיינר 22:16, 9 בנובמבר 2010 (IST)
בסדר גמור. לי יש בעיה בקטע של הגדרת שלילת הגבול, אם תוכל לצטט כאן (שוב) את ההגדרה אודה לך מאוד.
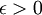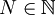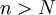כפי שההפך מהמשפט לכל סיר יש מכסה שמתאים לו הוא קיים סיר שכל המכסים אינם מתאימים לו, L אינו גבול של הסדרה a_n אם קיים \epsilon>0 כך שלכל N\in\mathbb{N} קיים n>N כך שמתקיים 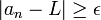|a_n-L|\geq\epsilon. --ארז שיינר 22:30, 9 בנובמבר 2010 (IST)
יש לי שאלה לגבי זה (לא גל)- אפילו שאני יודע ששלילת הגבול היא כמו שאמרת, לכל N קיים n>N, אבל למה לא הופכים שת הקיים n>N ל-לכל n<N כמו שאמר לנו המתרגל שבשלילת משפט, צריך להפוך כל קיים ל-לכל ולהפך (וכן להפוך כל אי שוויון)? כלומר איך יודעים איזה חלקים במשפט להפוך ואיזה לא? תודה!
לדעתי זה משום שרוצים להביא לסתירה עם הגדרת הגבול, ואם נהפוך את הסימן כפי שאמרת לא נקבל סתירה להגדרת הגבול. מעבר להפיכת הסימנים צריך להפוך בחוכמה, ולראות איזה שינוי סימן יעזור לסתור את ההגדרה ואיזה לא יעזור לסתור אותה.
מה שאמרת לא הגיוני, כי בזמן ששוללים את המשפט לא "יודעים" מתי נקבל סתירה להגדרת הגבול, זה מה שמנסים לעשות...
לכל הופך לקיים, קיים הופך ללכל ומתקיים הופך ללא מתקיים. לכן ההפך מ'מתקיים 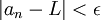|a_n-L|<\epsilon הוא 'מתקיים 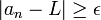|a_n-L|\geq \epsilon' כי זו השלילה של המשפט, אנחנו לא סתם מחליפים כל 'גדול' ב'קטן'. תחשוב על המשפט 'לכל המתרגלים קוראים ארז', ההפך שלו הוא 'יש מתרגלים ששמם אינו ארז'. שים לב שלא הפכנו את 'שמם' או 'ארז'. הופכים רק את קיים, לכל ומתקיים. --ארז שיינר 19:33, 10 בנובמבר 2010 (IST)
מה?? לא הבנתי את 2 החלקים הראשונים של תגובתך. חוץ מזה, צריך הרי להפוך גם את האי שוויונים, אז למה לא הופכים את ה"אפסילון גדול מאפס" ל"אפסילון קטן מאפס"? [אני יודע, מן הסתם, לפי האינטואיציה, שהמשפט הנכון הוא עם אפסילון גדול מאפס, ואם המשפט היה עם אפסילון קטן מאפס אז הוא לא היה הגיוני, אבל אני רק רוצה לדעת "למען הפרוטוקול" למה לא הופכים את הקטע עם האפסילון, בעוד שאמורים להפוך את האי שוויונים.] תודה
תקרא בבקשה שוב את דברי, במיוחד את הסיכום. לא צריך להפוך את אי השיוויונים. אי השיוויון התהפך רק מכיוון שהוא חלק ממשפט מתקיים ש... במקום לומר לא מתקיים n>3 אנו אומרים מתקיים n קטן שווה 3. אני חוזר שנית, הופכיים בלבד את 'לכל', 'קיים', ו'מתקיים'. --ארז שיינר 20:23, 10 בנובמבר 2010 (IST)
אבל הפכת את האי שוויון עם האפסילון, וכן כתוב לפני האי שוויון עם האפסילון "קיים"


היה רשום -

לכל אפסילון גדול מאפס קיים N כך שלכל n>N מתקיים an-L קטן מאפסילון.

לאחר השלילה, המשפט הינו:

קיים אפסילון גדול מאפס כך שלכל N קיים n>N כך שלא מתקיים an-L קטן מאפסילון.

זו השלילה, החלפנו רק את הלכל, קיים ומתקיים. כעת, ניתן לשים לב ש

לא מתקיים שan-L קטן מאפסילון 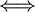\iff מתקיים שan-L גדול שווה אפסילון.

--ארז שיינר 21:21, 10 בנובמבר 2010 (IST)

תודה

תרגיל 4 שאלה 2

בשלב מסוים בהוכחה, הגעתי לשלב שבו צריך להוכיח שהגבול של 1 חלקי אינפימום של an שווה לאחד חלקי הגבול של (..). זה נכון וקל להוכיח (הוכחנו בהרצאה), חוץ מכשהאינפימום של an שווה 0, ואז זה לא נכון. מה לעשות- מותר להניח שהאינפימום של an לא שווה 0?

תשובה

לא מותר להניח את זה, הרי רק נתון שאיברי הסדרה גדולים מאפס, תיאורטית אולי הם שואפים לאפס? יש להוכיח שהוא אינו אפס אם רוצים להשתמש בזה. --ארז שיינר 12:53, 10 בנובמבר 2010 (IST)

אבל אי אפשר להוכיח שהוא אינו אפס- כי הוא יכול להיות אפס! למשל כשאיברי הסדרה הם 1/n!
האם \frac{1}{n} הינה סדרה שמקיימת את תנאי השאלה? --ארז שיינר 19:19, 10 בנובמבר 2010 (IST)
כן, כל האיברים גדולים מאחד (אלא אם אתה מתכוון לתנאי השני הזה)
אני מתכוון לכל התנאים בשאלה, מן הסתם. --ארז שיינר 19:56, 10 בנובמבר 2010 (IST)
אז אתה מתכוון שבעזרת הנתון (המסובך) הזה אני צריך להוכיח שהגבול הנ"ל אף פעם לא שווה אפס?
אין צורך להתעסק עם גבולות, יש רק inf וsup (ראה הגדרה בעמוד הראשי). זה מסובך ברמה של: נתון ab=1 הוכח a שונה מאפס. --ארז שיינר 20:27, 10 בנובמבר 2010 (IST)
אבל (נראה לי ש)זה לא נכון, ראשית כי כן צריך להשתמש בגבולות, מכיוון שהמשפט שאני צריך להסתמך עליו הוא שאם הגבול של סדרה שאיבריה שונים מאפס שואף לגבול ששונה מאפס אזי 1 חלקי הסדרה שואף לאחד חלקי הגבול; שנית כי הביטוי lim inf {an} = sup inf {an} לא מופיע בנתון, כלומר הוא לא אף אחד מ a או b במשפטך. סלך לי אם אני מציק, אני רק מנסה להבין בצורה נכונה!
אין צורך להשתמש במשפט שציינת (אריתמטיקה של גבולות), זה אפשרי, אבל לא חובה. אפשר להוכיח ישירות מההגדרה של liminf וlimsup ולשם מכוון הרמז כמובן. אני לא מבין מה הקשר בין השיוויון שרשמת למשהו, אבל בהחלט limsup an הוא אחד הביטויים במכפלה, ולכן שונה מאפס. --ארז שיינר 21:30, 10 בנובמבר 2010 (IST)
limsup an לא שווה לאפס על פי הנתון אבל זה לא עוזר לנו. צריך ש liminf an יהיה לא שווה לאפס. אי אפשר להוכיח את זה בעזרת הנתון!
אם אתה כל כך בטוח שלא ניתן להוכיח את זה, אתה מוזמן להביא דוגמא נגדית שמפריכה את זה. (או פשוט לעשות 'אחד-חלקי' בשני צידי המשוואה בסעיף a ואז להוכיח אותה...) --ארז שיינר 20:11, 11 בנובמבר 2010 (IST)
אני לא אומר שאי אפשר להוכיח את זה,,, אני אומר שאי אפשר להוכיח את זה איך שאמרת, בגלל שהנתון אומר לנו ש limsup an לא שווה אפס, אבל זה לא משנה לנו,,, אנחנו צריכים ש liminf an לא יהיה שווה לאפס!!
תקרא את ההערה שלי לגבי 'אחד-חלקי' ותראה שאתה לא צריך ישירות שliminf יהיה שונה מאפס (פשוט תתחיל מ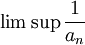\limsup \frac{1}{a_n}) --ארז שיינר 21:06, 11 בנובמבר 2010 (IST)

גבול חלקי

האם אפשר לומר שliminf של סדרה הוא החסם התחתון שלה בהכרח?

תשובה

לא. לסדרה אין חסם תחתון (אין כזו הגדרה) ניתן להסתכל על החסם התחתון של הקבוצה המכילה את כל איברי הסדרה, וגם אז התשובה היא לא. אם זה היה נכון, ההגדרה הייתה הרבה יותר פשוטה, לא? אנחנו לא מסבכים את העניינים סתם.

דוגמא נגדית: a_n=\frac{(-1)^n}{n}. גם הlimsup וגם הliminf של הסדרה שווים לאפס. אבל החסם העליון והתחתון של הקבוצה המכילה את איברי הסדרה הינם מינוס אחד וחצי. --ארז שיינר 19:22, 10 בנובמבר 2010 (IST)

תרגיל 4 שאלה 2

אני לא מבין איך אמורים להוכיח שהגבול שווה L, כלומר איך להוכיח שמגיעים לסתירה בשלילת הגבול, אם כל מה שידוע לנו שהגבול העליון והתחתון שווים לL. אף פעם לא למדנו על שום קשר בין הגבול של הסדרה לגבול העליון והתחתון ולכן התרגיל הזה הוא בגדר בלתי אפשרי בעליל.

למדנו שמספר הוא גבול חלקי של סדרה אם הוא גבול של תת סדרה שלה. למדנו את הגדרת שלילת הגבול. למדנו את משפט בולצנו וירשטראס. ולמדנו עוד הרבה דברים מגניבים. --ארז שיינר 21:47, 10 בנובמבר 2010 (IST)
ררררגע: אי אפשר להגיד ש 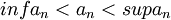inf{a_n}<a_n<sup{a_n} (קטן שווה לא קטן) ולכן עפ טענת הסנדביץ an שואף לL?
תלוי למה אתה מתכוון בביטויים שרשמת. מה זה inf\{a_n\} ? --ארז שיינר 19:15, 11 בנובמבר 2010 (IST)
האינפימום של an...?
an היא סדרה, לסדרה אין אינפימום. יש אינפימום לקבוצה המכילה את איברי הסדרה, מהכיוון הזה יכול להיות הגיון בדברים, ויש את הlimsup וliminf לגביהם אי השיוויון הנ"ל לא נכון באופן כללי. --ארז שיינר 20:14, 11 בנובמבר 2010 (IST)
כן ארז, האינפימום של הקבוצה שמכילה את הסדרה.
את כל הסדרה? כלומר 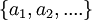\{a_1,a_2,....\}? אם כן אז אין לך נתונים על המספר הזה - הוא לא שווה לliminf או limsup. אם תגדיר אבל נכון, ותיקח גבול בשני הצדדים, אתה יכול לפתור את התרגיל. --ארז שיינר 20:59, 11 בנובמבר 2010 (IST)
התכוונתי של הקבוצה bn של כל איברי an מהמקום הn (כמו תמיד!!!!!!!!!!!!). ואפשר להגיד ש liminfan<an<limsupan לכן an שואף לL מ.ש.ל?
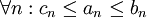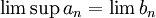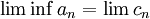אפשר לומר ש\forall n: c_n\leq a_n \leq b_n וכמו כן \limsup a_n = \lim b_n וגם \liminf a_n = \lim c_n ולכן סנדביץ ולכן משל. --ארז שיינר 22:06, 11 בנובמבר 2010 (IST)

שאלה 7 תרגיל 5

האם מדובר בסדרה שורש 5+....? אחרת מה המשמעות???

אני לא מבין את השאלה. --ארז שיינר 19:16, 11 בנובמבר 2010 (IST)

תרגיל 4 ש' 6

3 דברים לא מובנים: - לא צריך תנאי התחלה, אנחנו אמורים להביע את an כפונקציה של a1?

- מתכוונים שצריך להביע ממש את an כפונקציה של n (בלתי אפשרי) או שצריך להביע את a2n ואת a2n+1 כפונקציות של n?

- אם מצאתי כמה (מס סופי) של תת סדרות ששואפות לכמה גבולות, והסדרות האלה "מכסות" את כל an (אין לי כוח להגדרה מדויקת, זה היה בתרגול), אז לפי משפט מהתרגול אפשר להגיד שאלה כל הגבולות החלקיים של הפונקציה, כלומר סיימנו את התרגיל. אז מה צריך להוכיח באינדוקציה אם ככה, ולמה?


תשובה

-כן.

-זה אותו דבר, מה ההבדל? לצורך העניין - כן, למצוא נוסחא לזוגיים ונוסחא לאי-זוגיים.

-להוכיח את הנוסחא כפונקציה של n באינדוקציה.

זה בכלל לא אותו דבר. זה מטעה את הסטודנטים!
מהנסיון שלי סטודנטים טועים לבד. או במילים אחרות - נו באמת. --ארז שיינר 20:06, 11 בנובמבר 2010 (IST)

תרגיל 5 לבוחן?

אני בקבוצה של אדוארד ואצלו צריך להגיש את תרגיל 4 ביום ראשון הקרוב, שזהו גם היום בו יתקיים הבוחן.

אז השאלה היא אם כדאי כהכנה לבוחן לעשות גם את תרגיל 5, האם הוא מתאים בחומר שלו?

אני לא יודע לגבי הקבוצה של אדוארד. אני לומד אצל אפי, ואצלנו תרגיל 5 כן מתאים לבוחן, למרות שביום הבוחן נגיש גם אנחנו רק את תרגיל 4. גל א.
טוב, תודה. זה אותו הבוחן, לא?
לא יודע, תלוי אם הוא יכלול גם את מה שאתם למדתם על חתכי דדקינד וכל אלה (שאצל ד"ר הורוביץ הם לא נלמדו עדיין). אם כן - אז וודאי שהבחנים יהיהו שונים. אם לא - ייתכן שהם יהיו זהים. גל א.
מקור: https://math-wiki.com/index.php?title=שיחה:88-132_סמסטר_א%27_תשעא&oldid=7414