הבדלים בין גרסאות בדף "שיחה:88-113 סמסטר א' תשעא/קבוצת דיון-עדי ניב"
(←שאלה חשובה לגבי 1.9) |
|||
| שורה 127: | שורה 127: | ||
'''כלומר הם הוקטורים הסט' הרגילים עם מקדמים מעל שדה המרוכבים | '''כלומר הם הוקטורים הסט' הרגילים עם מקדמים מעל שדה המרוכבים | ||
:ז"א שהצמוד של e1 שווה לe1, נכון? | :ז"א שהצמוד של e1 שווה לe1, נכון? | ||
| + | |||
| + | '''כן, באופן כללי הצמוד של <math>ke_1</math> הוא הצמוד של k כפול <math>e_1</math>. | ||
| + | |||
| + | '''למה זה רלוונטי לשאלה זו. | ||
גרסה מ־08:42, 27 בנובמבר 2010
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
למה?
הדט' של פ"מ שווה לפ"מ בחזקת n??
מה?
- ד"ר צבאן כתב שהדט' של פולינום מינימלי שווה לפולינום המימינלי (כפול I) בחזקתn (http://math-wiki.com/images/9/9b/Charpolydivminpoly%5En.pdf, סוף המסמך), ואני שאלתי- למה זה? תודה!
נכונות טענה
שלום רב,
האם הטענה הבאה נכונה: "אם שתי מטריצות דומות זו לזו, אז יש להן אותם פולינום האופייני ופולינום המינימלי. לכן, כדי שמטריצה תהיה לכסינה, צריכים להיות לה פולינום אופייני ומינימלי זהים לאלו של מטריצה אלכסונית". במילים אחרות, הטענה אומרת שמטריצה  (מגודל
(מגודל 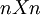 ) לכסינה אם:
) לכסינה אם:
1.  כאשר
כאשר 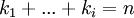
2.  .
.
תודה! גל א.
- קשר בין לכסינות לבין הפולינום המינימלי --ארז שיינר 22:02, 22 בנובמבר 2010 (IST)
עדי: תסתכל בארכיון2, עניתי על זה, ריבויי שורשי הפ"א הם 1 בפ"מ. שזה גם מה שאומר המשפט של ארז ושלך. כן, אפשר להשתמש בזה, למדנו את זה גם בתירגול.
5.22 לגבי ה-trace
שלום רב, אני חושב שאני יודע איך ה-trace של המט', אך רק מתוך אינטואיציה, מישהו יכול להיות אולי רמז לדרך הפתרון? תודה שקד רטר
עדי: חשוב על משהו אחר שמשותף למט' דומות והסק מסקנה על העיקבה שלהן תודה!!! שקד רטר 09:54, 23 בנובמבר 2010 (IST)
תיקונים בחוברת של ד"ר צבאן
בעמ' 95 תרגיל 1.1, אמור להיות כתוב u,v "עם או בלי אינדקסים" במקום "עם או בלי סקלרים", נכון? והחלק שיותר חשוב לשיעורי הבית, ב1.4 ב' ו-ג', המ"פ הן מתרגיל 1.3, לא 1.1, נכון? תודה
עדי: 1.1:כן.
1.4:גם כן.
שאלה 1.9
מה הם הוקטורים הסטנדרטיים ב  ? (כלומר e_1 לדוגמה, שווה ל
? (כלומר e_1 לדוגמה, שווה ל  או למשהו אחר?)
עריכה-עוד שאלה בנושא: האם ניתן להתייחס לוקטורים הסט' ei כוקטורי שורות? כי אם לא, אז יהיה חלק בתרגיל שיהיה קשה לביצוע, מכיוון שv הוא סכום של וקטורי עמודות, וכדי לכפול אותו במטריצה מימין יש להתייחס לשורותיו ולא לעמודותיו... תודה!
או למשהו אחר?)
עריכה-עוד שאלה בנושא: האם ניתן להתייחס לוקטורים הסט' ei כוקטורי שורות? כי אם לא, אז יהיה חלק בתרגיל שיהיה קשה לביצוע, מכיוון שv הוא סכום של וקטורי עמודות, וכדי לכפול אותו במטריצה מימין יש להתייחס לשורותיו ולא לעמודותיו... תודה!
- אני לא מתרגל, אבל לדעתי הרעיון בוקטרים מעל שדה הוא שיש לך, כמו שאמרת, את הוקטורים e1, e2, ... en מעל כל שדה, וזה שיש לך i לא אמור לשנות לך.
- לא הבנתי...
עדי:נכון מאוד. הכוונה שאתה יכול ליצור כל וקטור מרוכב מצרוף לינארי של e1,...,en כאשר i הוא אחר הסקלרים האפשריים.
לגבי החלק השני, למה החלטת שאלו וקטורי עמודות? כמובן שאם דורשים  אז הוקטורים מוגדרים כך שהמכפלה ביניהם מוגדרת.
אז הוקטורים מוגדרים כך שהמכפלה ביניהם מוגדרת.
- פעלתי לפי הרמז, וכדי לחשב את האגף עם המטריצות, צריך לעשות את כפל A עם v משמאל- ולפי הרמז, צריך לכתוב את v כסכום של הוקטורים הסטנדרטיים, שבדרך כלל אנחנו מתייחסים אליהם כוקטורי עמודה ולא שורה, ולכן שאלתי אם אפשר הפעם להתחייס אליהם כוקטורי שורה. אם כן אפשר להתחייס אליהם כוקטורי שורה, אז נראה לי שצריך להשתמש בכפל שורה שורה כדי לבדוק את הכפל... לא?(ראי שאלה למטה).
למה וקטור שורה כפול מטריצה הוא שורה שורה? עושים כרגיל שורה כפול עמודה ומקבלים שוב וקטור.
- תודה!
כפל שורה שורה
מישהו יכול בבקשה לרשום את החוק "כפל שורה-שורה"? (אם אני זוכר נכון יש לו 2 סעיפים). אני לא מצליח למצוא אותו בשום מקום. תודה!
בקשר למה זה?
- חשבתי לנסות להשתמש בזה בתרגיל 1.9, בכפל v עם A.
אז למה שורה-שורה? תפעל לפי הרמז, לפני שאתה ניגש לפיתרון היזכר מה משאירה מכפלה של מטריצה בוקטור שורה 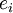 משמאל ומה משאירה מכפלה של מטריצה בוקטור עמודה
משמאל ומה משאירה מכפלה של מטריצה בוקטור עמודה  מימין.
מימין.
שאלה 1.13
השאלה אומרת שיש שלושה וקטורים שבמכפלה פנימית עם עצמם שווים ל- 1- ועם אחד מהאחרים שווים ל- 3. צ"ל שסכומם הוא אפס. הכוונה בתרגיל היא שיש מרחב מכפלה פנימית שפועל כך או שאלו ארבע וקטורים מיוחדים במכפלה הסטנדרטית שמקיימים את התנאים? או אלי בכלל אנחנו לא יודעים על איזו מכפלה סקלרית מדובר וצריך להוכיח רק לפי ההגדרות?
תודה מראש!
עדי: לא עבור מכפלה ספציפית. עבור מ"פ כלשהי על 4 וקטורים ספציפיים. כן,לפי הגדרות.
1.13
אפשר רמז לתרגיל 1.13? אין לי מושג מאיפה להתחיל בכלל...
- תנסה לחשב את המכפלה הפנימית של סכום ארבעת הוקטורים ;)
- ווואי פתאום זה כל כך קל! תודה רבה!!!
- בכיף ;)
- ווואי פתאום זה כל כך קל! תודה רבה!!!
הרצאה ותרגול בחנוכה
האם יתקיימו הרצאה ושיעור תרגול בחנוכה?
- לקבוצה של ד"ר צבאן לא יתקיימו שיעורים בלינארית בכלל, רק התרגול באינפי שנקבע מולנו. גל
עדי: בעיקרון זה תלוי בהספק שלנו בתירגול הקרוב אבל כפי שנראה כרגע לא, רק בוחן ב9/12.
עבודת ההגשה לחנוכה
איפה היא? לא מצאתי אותה בעמוד הראשי, למרות שכתוב שהיא נמצאת שם. אור שחףשיחה 18:56, 25 בנובמבר 2010 (IST)
בתרגילים
1.9- הבהרה
האם הכוונה ב- 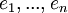 היא לווקטורי הבסיס הסטנדרטי?
היא לווקטורי הבסיס הסטנדרטי?
כן
שאלה חשובה לגבי 1.9
אפשר בבקשה מהם הוקטורים הסטנדרטיים בC^n במפורש? זה חשוב, כדי צריך לדעת מהם הצמודים להם. לדוגמה, אם הוקטורים הסט' בC הם כמו בR, כלומר 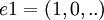 וכו', אז הצמוד של זה הוא הוקטור עצמו, אבל הוקטור הסט' בC הוא
וכו', אז הצמוד של זה הוא הוקטור עצמו, אבל הוקטור הסט' בC הוא 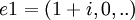 אז כבר הצמוד של זה הוא משהו אחר. תודה מראש
אז כבר הצמוד של זה הוא משהו אחר. תודה מראש
עדי:
 כלומר הם הוקטורים הסט' הרגילים עם מקדמים מעל שדה המרוכבים
כלומר הם הוקטורים הסט' הרגילים עם מקדמים מעל שדה המרוכבים
- ז"א שהצמוד של e1 שווה לe1, נכון?
כן, באופן כללי הצמוד של 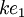 הוא הצמוד של k כפול
הוא הצמוד של k כפול 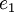 .
.
למה זה רלוונטי לשאלה זו.
 וזו מטריצה אלכסונית, לכן = למכפלת אברי האלכסון הראשי.
וזו מטריצה אלכסונית, לכן = למכפלת אברי האלכסון הראשי.