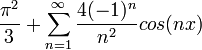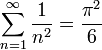הבדלים בין גרסאות בדף "אנליזת פורייה - ארז שיינר"
מתוך Math-Wiki
(←חישובים להקדמה) |
|||
| שורה 3: | שורה 3: | ||
=תקציר ההרצאות= | =תקציר ההרצאות= | ||
| − | ==הקדמה== | + | ==הרצאה 1 - הקדמה ומקדמי פוריה== |
| − | ===גלים=== | + | ===הקדמה - גלים=== |
| + | |||
*מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית. | *מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית. | ||
*לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות: | *לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות: | ||
| שורה 43: | שורה 44: | ||
*במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו. | *במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו. | ||
| − | ==טורי פורייה== | + | ===טורי פורייה ומקדמי פוריה=== |
*טור פורייה הוא טור מהצורה <math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]</math> | *טור פורייה הוא טור מהצורה <math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]</math> | ||
| שורה 50: | שורה 51: | ||
| − | ===חישובים להקדמה=== | + | ====חישובים להקדמה==== |
*ראשית נזכור את הנוסחאות הטריגונומטריות: | *ראשית נזכור את הנוסחאות הטריגונומטריות: | ||
**<math>\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]</math> | **<math>\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]</math> | ||
| שורה 74: | שורה 75: | ||
**למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | **למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | ||
| − | ===מקדמי הטור=== | + | ====מקדמי הטור==== |
*כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש. | *כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש. | ||
| שורה 101: | שורה 102: | ||
| − | ====דוגמא==== | + | =====דוגמא===== |
*נחשב את מקדמי הפורייה של ההמשך המחזורי של <math>x^2</math> | *נחשב את מקדמי הפורייה של ההמשך המחזורי של <math>x^2</math> | ||
*שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל. | *שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל. | ||
| שורה 132: | שורה 133: | ||
| + | ==הרצאה 2 - למת רימן לבג, גרעין דיריכלה== | ||
===תזכורת לגבי מרחבי מכפלה פנימית והיטלים=== | ===תזכורת לגבי מרחבי מכפלה פנימית והיטלים=== | ||
*E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין <math>f:[-\pi,\pi]\to\mathbb{C}</math> מעל השדה <math>\mathbb{C}</math>. | *E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין <math>f:[-\pi,\pi]\to\mathbb{C}</math> מעל השדה <math>\mathbb{C}</math>. | ||
גרסה מ־11:10, 25 בפברואר 2019
תוכן עניינים
מבחנים לדוגמא
תקציר ההרצאות
הרצאה 1 - הקדמה ומקדמי פוריה
הקדמה - גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה
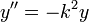 המתארת תנועה על מסה המחוברת לקפיץ
המתארת תנועה על מסה המחוברת לקפיץ - זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
- הפתרון הכללי למד"ר הוא
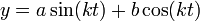 .
. - הקבוע
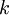 קובע את התדר של כל גל.
קובע את התדר של כל גל. - הקבועים
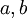 קובעים את האמפליטודה של כל גל.
קובעים את האמפליטודה של כל גל. - מה לגבי הפאזה?
- בפונקציה
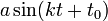 , הקבוע
, הקבוע 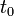 קובע את הפאזה.
קובע את הפאזה. - ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- בפונקציה
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי
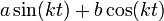 ניתן להציג כגל יחיד?
ניתן להציג כגל יחיד? - תשובה: כן.
- הוכחה:
- נסמן
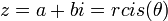
- כלומר
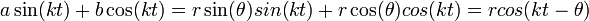
- נסמן
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא
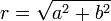 .
.
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.
טורי פורייה ומקדמי פוריה
- טור פורייה הוא טור מהצורה
![f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]](/images/math/6/6/c/66c1bbf99995adc693d0394e5f637359.png)
- אם פונקציה שווה לטור פורייה שלה, מהם המקדמים
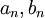 ?
?
חישובים להקדמה
- ראשית נזכור את הנוסחאות הטריגונומטריות:
- כעת, לכל
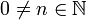 נקבל:
נקבל:
- עבור
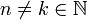 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0](/images/math/8/f/b/8fbca5cb5a1f31c0bdbb8c0c68cc16b9.png)
- שימו לב כי השתמשנו כאן בעובדה ש
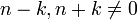 .
.
- באופן דומה, לכל
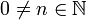 נקבל:
נקבל:
- עבור
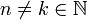 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n+k}+\frac{\sin((n-k)x)}{n+k}\right]_{-\pi}^{\pi}=0](/images/math/c/b/8/cb8185051d01ace1ce544fcb4147f83b.png)
- שימו לב כי השתמשנו כאן בעובדה ש
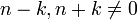 .
.
- עבור
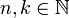 נקבל:
נקבל:
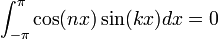 כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
- ולבסוף, עבור
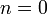 נקבל
נקבל
- שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.
- הערה חשובה:
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
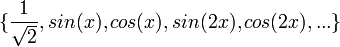 מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית
מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית 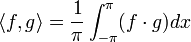
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
מקדמי הטור
- כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
![\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx=](/images/math/a/1/8/a18fda320cac6333a54d8dc7285a69f2.png)
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx=](/images/math/6/a/9/6a94fbbbdf98411fd913d8c54bf08f53.png)
- כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right]](/images/math/0/e/8/0e840fbc166461424acf8a0a238acdc2.png)
- לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
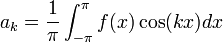
- שימו לב שחישוב זה נכון בפרט עבור
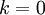 .
. - באופן דומה נקבל כי
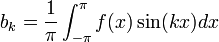
- הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
- השאלה היא אילו פונקציות שוות לטור פורייה.
- באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור
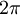 .
. - לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
- תהי פונקציה
 , נגדיר את ההמשך המחזורי שלה
, נגדיר את ההמשך המחזורי שלה 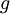 על ידי:
על ידי: - לכל
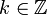 ולכל
ולכל 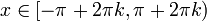 נגדיר
נגדיר 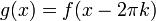 .
. - ברור ש
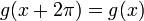 , כלומר קיבלנו פונקציה מחזורית.
, כלומר קיבלנו פונקציה מחזורית. - ניתן גם לרשום בנוסחא מקוצרת
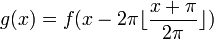
- תהי פונקציה
- לדוגמא, ההמשך המחזורי של
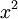 :
:
דוגמא
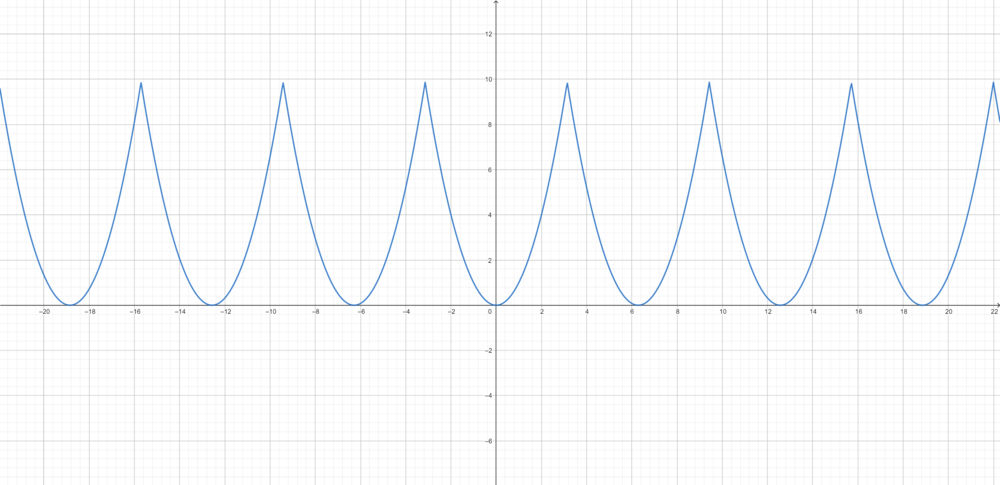
- נחשב את מקדמי הפורייה של ההמשך המחזורי של
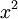
- שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.
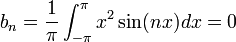 .
.
- שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.
- שימו לב כי לכל
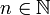 מתקיים כי
מתקיים כי 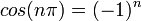
- סה"כ אם ההמשך המחזורי של
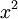 שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
- נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב
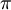 .
. 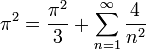
- ונקבל את הסכום המפורסם
הרצאה 2 - למת רימן לבג, גרעין דיריכלה
תזכורת לגבי מרחבי מכפלה פנימית והיטלים
- E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין
![f:[-\pi,\pi]\to\mathbb{C}](/images/math/2/c/b/2cb36383da87b746f0502644a80815b8.png) מעל השדה
מעל השדה 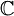 .
.
- פונקציה רציפה למקוטעין היא פונקציה רציפה פרט למספר סופי של נקודות אי רציפות סליקות או קפיצתיות (מין ראשון).
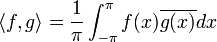 היא מכפלה פנימית מעל E.
היא מכפלה פנימית מעל E.- נביט בנורמה המושרית
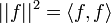
- תהי קבוצה אורתונורמלית סופית
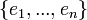 הפורשת את המרחב W.
הפורשת את המרחב W. - לכל וקטור
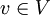 נגדיר את ההיטל של
נגדיר את ההיטל של 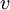 על W על ידי
על W על ידי 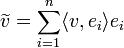
- מתקיים כי
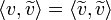
- הוכחה
- מתקיים כי
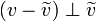
- הוכחה
- מתקיים כי
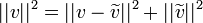
- הוכחה
- מסקנה חשובה:
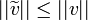
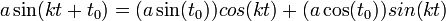
![\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]](/images/math/2/5/f/25f8d4d6c77a138100c89a987596ad1a.png)
![\cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right]](/images/math/f/4/9/f49ffa386014bd9ab57625ca1919dc7d.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1](/images/math/7/9/b/79b96630be4b13a139e89a28e5c3417b.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1](/images/math/2/7/b/27bf3f269b2c1bad9a888e32febb6afb.png)
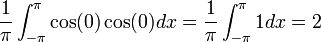
![a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3}](/images/math/6/6/f/66f8ca0042ee471a64c81bf7579cf761.png)
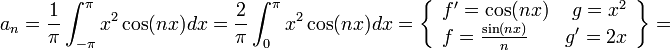
![=\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx=
\left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}=](/images/math/5/1/5/515fbb2ba109a06847f638fe4e5c9362.png)
![- \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2}](/images/math/9/6/2/9628cd82e657ebc65624a51d3a39dcb9.png)