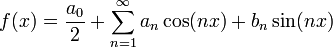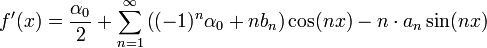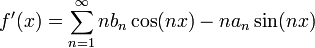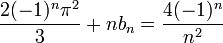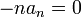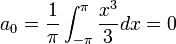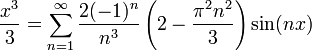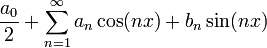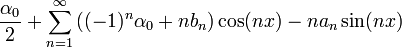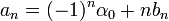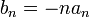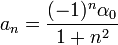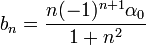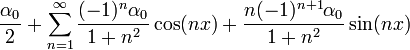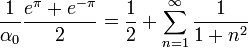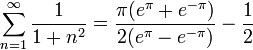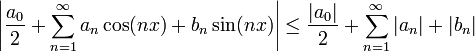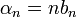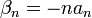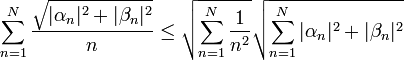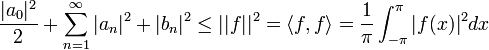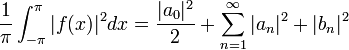הבדלים בין גרסאות בדף "אנליזת פורייה - ארז שיינר"
מתוך Math-Wiki
(←תנאי להתכנסות במ"ש של טור פורייה) |
(←הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש) |
||
| שורה 523: | שורה 523: | ||
====הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש==== | ====הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש==== | ||
| + | *תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> המקיימת <math>f(-\pi)=f(\pi)</math>. | ||
גרסה מ־08:24, 11 במרץ 2019
תוכן עניינים
מבחנים לדוגמא
תקציר ההרצאות
- ההרצאות מבוססות בחלקן על הספר המצויין 'טורי פוריה' של זעפרני ופינקוס.
הרצאה 1 - הקדמה ומקדמי פוריה
הקדמה - גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה
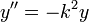 המתארת תנועה על מסה המחוברת לקפיץ
המתארת תנועה על מסה המחוברת לקפיץ - זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
- הפתרון הכללי למד"ר הוא
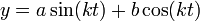 .
. - הקבוע
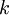 קובע את התדר של כל גל.
קובע את התדר של כל גל. - הקבועים
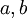 קובעים את האמפליטודה של כל גל.
קובעים את האמפליטודה של כל גל. - מה לגבי הפאזה?
- בפונקציה
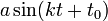 , הקבוע
, הקבוע 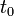 קובע את הפאזה.
קובע את הפאזה. - ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- בפונקציה
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי
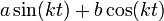 ניתן להציג כגל יחיד?
ניתן להציג כגל יחיד? - תשובה: כן.
- הוכחה:
- נסמן
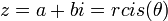
- כלומר
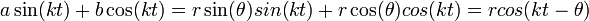
- נסמן
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא
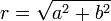 .
.
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.
טורי פורייה ומקדמי פוריה
- טור פורייה הוא טור מהצורה
![f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]](/images/math/6/6/c/66c1bbf99995adc693d0394e5f637359.png)
- אם פונקציה שווה לטור פורייה שלה, מהם המקדמים
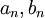 ?
?
חישובים להקדמה
- ראשית נזכור את הנוסחאות הטריגונומטריות:
- כעת, לכל
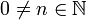 נקבל:
נקבל:
- עבור
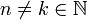 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0](/images/math/8/f/b/8fbca5cb5a1f31c0bdbb8c0c68cc16b9.png)
- שימו לב כי השתמשנו כאן בעובדה ש
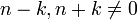 .
.
- באופן דומה, לכל
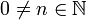 נקבל:
נקבל:
- עבור
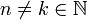 נקבל:
נקבל:
![\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n+k}+\frac{\sin((n-k)x)}{n+k}\right]_{-\pi}^{\pi}=0](/images/math/c/b/8/cb8185051d01ace1ce544fcb4147f83b.png)
- שימו לב כי השתמשנו כאן בעובדה ש
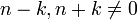 .
.
- עבור
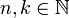 נקבל:
נקבל:
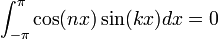 כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
- ולבסוף, עבור
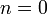 נקבל
נקבל
- שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.
- הערה חשובה:
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
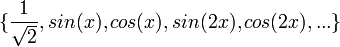 מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית
מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית 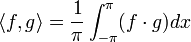
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה
מקדמי הטור
- כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
![\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx=](/images/math/a/1/8/a18fda320cac6333a54d8dc7285a69f2.png)
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx=](/images/math/6/a/9/6a94fbbbdf98411fd913d8c54bf08f53.png)
- כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
![=\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right]](/images/math/0/e/8/0e840fbc166461424acf8a0a238acdc2.png)
- לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
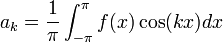
- שימו לב שחישוב זה נכון בפרט עבור
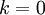 .
. - באופן דומה נקבל כי
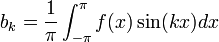
- הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
- השאלה היא אילו פונקציות שוות לטור פורייה.
- באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור
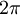 .
. - לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
- תהי פונקציה
 , נגדיר את ההמשך המחזורי שלה
, נגדיר את ההמשך המחזורי שלה 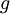 על ידי:
על ידי: - לכל
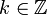 ולכל
ולכל 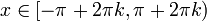 נגדיר
נגדיר 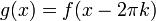 .
. - ברור ש
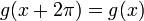 , כלומר קיבלנו פונקציה מחזורית.
, כלומר קיבלנו פונקציה מחזורית. - ניתן גם לרשום בנוסחא מקוצרת
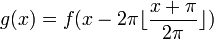
- תהי פונקציה
- לדוגמא, ההמשך המחזורי של
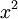 :
:
דוגמא
- נחשב את מקדמי הפורייה של ההמשך המחזורי של
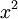
- שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.
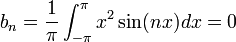 .
.
- שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.
- שימו לב כי לכל
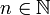 מתקיים כי
מתקיים כי 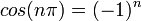
- סה"כ אם ההמשך המחזורי של
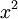 שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
- נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב
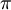 .
. 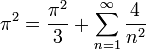
- ונקבל את הסכום המפורסם
הרצאה 2 - למת רימן לבג, גרעין דיריכלה
מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים
- פונקציה נקראת רציפה למקוטעין בקטע סופי אם:
- 1. היא רציפה פרט אולי למספר סופי של נקודות.
- 2. הגבולות החד צדדיים הרלוונטיים בכל נקודה הם סופיים.
- למעשה נקודות אי הרציפות היחידות של פונקציה רציפה למקוטעין הן ממין ראשון (קפיצתיות).
- פונקציה נקראת רציפה למקוטעין בקטע כללי, אם ניתן לחלק אותו לקטעים סופיים בהן הפונקציה רציפה למקוטעין.
- E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין
![f:[-\pi,\pi]\to\mathbb{C}](/images/math/2/c/b/2cb36383da87b746f0502644a80815b8.png) מעל השדה
מעל השדה 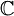 , המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
, המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
- לא קשה להוכיח שאכן מדובר במרחב וקטורי. בעיקר יש לשים לב לכך שסכום פונקציות בקבוצה נשאר בקבוצה.
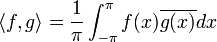 היא מכפלה פנימית מעל E.
היא מכפלה פנימית מעל E.
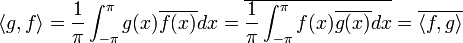
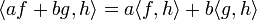
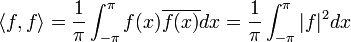
- בכל קטע רציפות האינטגרל על פונקציה חיובית הוא אפס אם ורק אם היא אפס.
- כיוון שהפונקציה בכל נקודה שווה לאחד הגבולות החד צדדיים או לממוצע בניהם, נובע שאם האינטגרל לעיל מתאפס הפונקציה חייבת להתאפס לחלוטין.
- נביט בנורמה המושרית
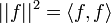
- כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית.
- יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד).
- ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית.
- תהי קבוצה אורתונורמלית סופית
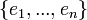 , ונקרא למרחב שהיא פורשת W.
, ונקרא למרחב שהיא פורשת W. - לכל וקטור
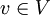 נגדיר את ההיטל של
נגדיר את ההיטל של 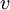 על W על ידי
על W על ידי 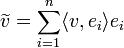
- נוכיח מספר תכונות לגבי ההיטל הזה:
- מתקיים כי
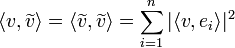
- הוכחה:
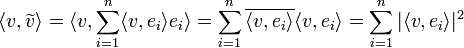
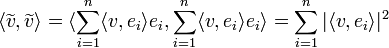
- המעבר האחרון נכון כיוון ש
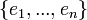 אורתונורמלית.
אורתונורמלית.
- מתקיים כי
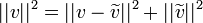
- הוכחה:
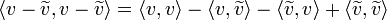
- נזכור כי
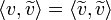 .
. - לכן קיבלנו כי
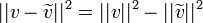
- מסקנה מיידית:
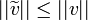
אי שיוויון בסל
- כעת תהי קבוצה אורתונורמלית אינסופית
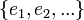 .
. - לכל
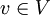 מתקיים כי
מתקיים כי 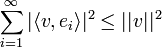
- הוכחה:
- ראינו שלכל n מתקיים כי
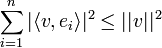 .
. - כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי
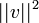 ולכן הטור מתכנס למספר שקטן או שווה לו.
ולכן הטור מתכנס למספר שקטן או שווה לו.
- בפרט נובע כי
למת רימן לבג
- ראינו כי
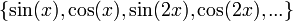 היא קבוצה אורתונורמלית ב
היא קבוצה אורתונורמלית ב (כרגע אנו לא צריכים את הפונקציה הקבועה).
(כרגע אנו לא צריכים את הפונקציה הקבועה). - כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י:
- לכל
 הגדרנו
הגדרנו 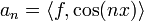 , ו
, ו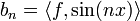
- נובע מאי שיוויון בסל כי המקדמים שואפים לאפס.
- כלומר:
- למת רימן-לבג: תהי
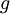 רציפה למקוטעין בקטע
רציפה למקוטעין בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) , אזי:
, אזי:
- הוכחה:
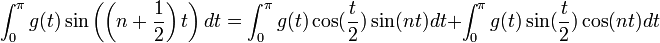
- נגדיר את שתי הפונקציות
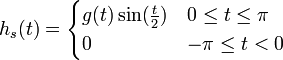 ו
ו 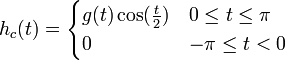
- קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי
 .
. - ביחד נקבל כי
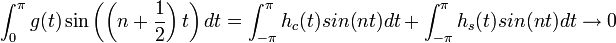
גרעין דיריכלה
- גרעין דיריכלה הוא הפונקציה
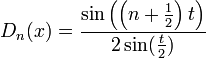
- טענה:
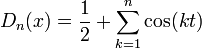 בכל נקודה
בכל נקודה 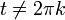
- הוכחה:
- נכפל ב
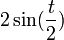 ונקבל בצד שמאל:
ונקבל בצד שמאל: 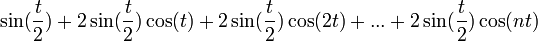
- נבחין בזהות הטריגונומטרית
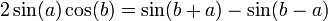
- ובפרט
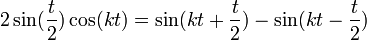
- ביחד נקבל

- נשים לב כי הפונקציה
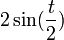 מתאפסת בנקודות
מתאפסת בנקודות 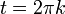 , בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה.
, בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה. - זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה.
- כמו כן, גרעין דיריכלה מחזורי
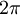 כיוון שהוא סכום של פונקציות מחזוריות
כיוון שהוא סכום של פונקציות מחזוריות 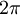 .
.
- נחשב את האינטגרל על גרעין דיריכלה:
- ראשית, לכל
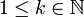 מתקיים:
מתקיים:
- לכן נקבל:
הסכומים החלקיים של טור פוריה
- תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה
 שהיא מחזורית
שהיא מחזורית 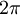 :
:
- נציב את מקדמי פוריה ונקבל כי:
- זה בעצם גרעין דיריכלה, כלומר קיבלנו כי:
- שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה.
- טענה: תהי
 פונקציה מחזורית
פונקציה מחזורית 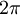 . אזי לכל
. אזי לכל 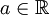 מתקיים כי:
מתקיים כי:
- כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך
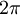 .
.
- הוכחה:
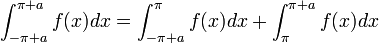
- נבצע הצבה
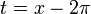 באינטגרל השני ונקבל:
באינטגרל השני ונקבל: 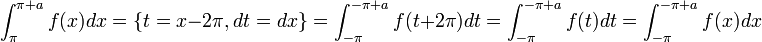
- ביחד נקבל כי:
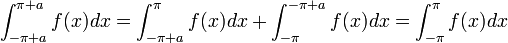
- נחזור לסכומים החלקיים ונבצע הצבה:

- כיוון שגרעין דיריכלה ו
 הן מחזוריות, נקבל:
הן מחזוריות, נקבל: 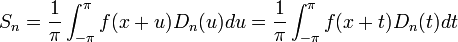
הרצאה 3 התכנסות נקודתית של טורי פוריה
סימונים והגדרות
- נסמן את הגבול החד צדדי מימין ב
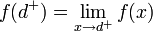 .
. - נסמן את הגבול החד צדדי משמאל ב
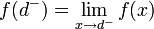 .
. - שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים.
- נגדיר את הנגזרת הימנית ע"י
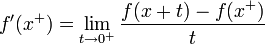 .
. - נגדיר את הנגזרת השמאלית ע"י
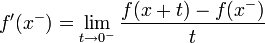 .
. - שימו לב: ייתכן ש
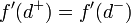 אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
דוגמא:
- נביט בפונקציה
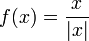
- מתקיים כי
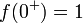 , ו
, ו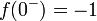 .
. - כמו כן מתקיים כי
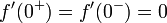 .
.
כמובן שהפונקציה אינה רציפה ואינה גזירה ב0.
משפט דיריכלה - התכנסות נקודתית של טור פוריה
- תהי
 פונקציה מחזורית
פונקציה מחזורית 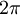 , רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות.
, רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות. - אזי לכל
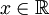 הטור עם מקדמי הפוריה של
הטור עם מקדמי הפוריה של  מתכנס:
מתכנס:
- בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל.
הוכחה
- תהי נקודה
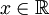 .
. - נביט בפונקציה
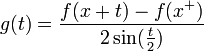
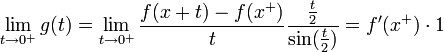
- כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש
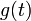 רציפה למקוטעין בקטע
רציפה למקוטעין בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) .
. - לפי למת רימן-לבג נובע כי:
- כלומר:
- כיוון ש
- נובע כי:
- באופן דומה לחלוטין ניתן להוכיח כי:
- ולכן סה"כ נקבל כי:
דוגמאות
דוגמא 1
- תהי
 ההמשך המחזורי של
ההמשך המחזורי של  .
.
- כיוון שf רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות (כולן שוות 1), תנאי משפט דיריכלה מתקיימים.
- כיוון שf הינה אי-זוגית, לכל
 מתקיים כי
מתקיים כי 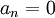 .
.
- כעת נחשב את המקדמים של הסינוסים:
- לכן, בכל נקודת רציפות של f, כלומר בכל נקודה
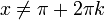 , מתקיים כי:
, מתקיים כי:
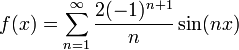 .
.
- בפרט, לכל נקודה
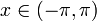 מתקיים כי:
מתקיים כי:
- עבור נקודות אי הרציפות (הקפיצתיות), מתקיים כי הממוצע בין הגבולות החד צדדיים הוא אפס.
- קל לראות שאכן לכל
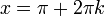 נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
- נציב לדוגמא
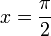 ונקבל:
ונקבל:
- לכל n זוגי הסינוס יתאפס, ולכן נקבל:
- שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של
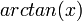 .
.
דוגמא 2
- כעת, תהי
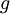 ההמשך המחזורי של
ההמשך המחזורי של 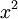 .
. - הפונקציה g הינה רציפה בכל הממשיים.
- הפונקציה g גזירה בכל הממשיים פרט לנקודות
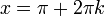 .
. - בנקודות אי הגזירות, הנגזרות החד צדדיות קיימות ושוות ל
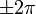 (כיוון שהנגזרת של
(כיוון שהנגזרת של 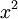 היא
היא 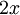 ).
). - סה"כ לפי משפט דיריכלה, טור הפוריה של g מתכנס אליה בכל הממשיים (כיוון שהיא רציפה בכל הממשיים).
- כלומר קיבלנו שלכל
![x\in [-\pi,\pi]](/images/math/c/8/2/c8293d1bbeed341c917b0834713a1b73.png) מתקיים כי:
מתקיים כי:
- שימו לב שאם נגזור איבר איבר את טור הפוריה של
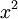 , נקבל את טור הפורייה של
, נקבל את טור הפורייה של 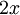 .
. - האם זה מפתיע?
דוגמא 3
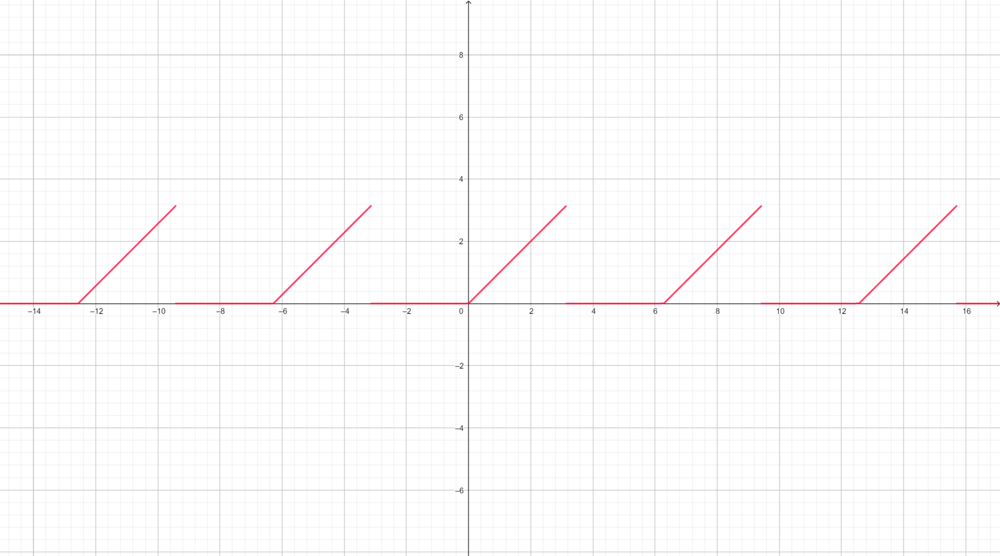
- תהי
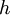 ההמשך המחזורי של הפונקציה
ההמשך המחזורי של הפונקציה ![\begin{cases}x & x\in [0,\pi]\\0 & x\in [-\pi,0)\end{cases}](/images/math/7/b/d/7bdd60b977bad799c8307881d2e07e0e.png)
- שוב, קיבלנו פונקציה רציפה למקוטעין עם נגזרות חד צדדיות קיימות וסופיות.
- נחשב את מקדמי הפורייה:
- סה"כ שלכל
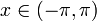 מתקיים כי:
מתקיים כי:
- שימו לב: מצאנו שני טורי פורייה שמתכנסים ל
 בקטע
בקטע 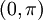 .
. - באופן דומה אפשר להראות שקיימים אינסוף טורי פורייה כאלה.
טור הנגזרת
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) כך שהנגזרת שלה
כך שהנגזרת שלה 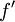 רציפה למקוטעין בקטע.
רציפה למקוטעין בקטע.
שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים
- שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ:
- כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות.
- בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ.
- אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, מרבית ערכי f יצטמצמו, ונשאר רק עם הקצוות.
- לדוגמא:
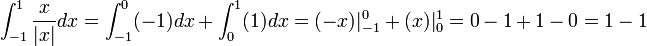
- כלומר קיבלנו כי
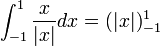 , כאשר
, כאשר 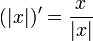
חישוב מקדמי טור הפורייה של הנגזרת
- נסמן את מקדמי הפורייה של
 ב
ב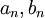
- נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב
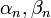 :
:
- כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו:
- אזי טור הפורייה של הנגזרת הינו:
- במקרה המיוחד בו
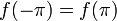 מתקיים כי
מתקיים כי 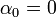 ולכן נקבל את טור הפורייה הפשוט:
ולכן נקבל את טור הפורייה הפשוט:
דוגמאות
דוגמא 1
- נזכר בטור הפורייה של
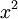 :
:
- נרצה למצוא את מקדמי הפוריה של
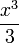 , נסמנם ב
, נסמנם ב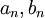 .
.
- לכל
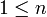 נקבל כי:
נקבל כי:
- כמו כן נחשב את המקדם הראשון:
- נחלץ את המקדמים ונקבל כי טור הפורייה של
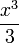 הוא:
הוא:
דוגמא 2
- נחשב את טור הפורייה של
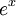 .
. - נסמן את טור הפורייה של
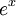 ב:
ב:
- כמובן שהנגזרת במקרה הזה שווה לפונקציה, ולכן יש לה בדיוק אותו טור פורייה.
- מצד שני, טור הפורייה של הנגזרת צריך להיות:
- כאשר
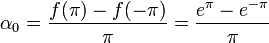
- ביחד נקבל את המשוואות:
- נציב את המשוואה השלישית בשנייה ונקבל:
- ולכן
- סה"כ קיבלנו כי טור הפורייה של
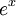 הינו:
הינו:
- כיוון שלהמשך המחזורי של
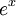 יש אי רציפות קפיצתית ב
יש אי רציפות קפיצתית ב , טור הפורייה שם מתכנס לממוצע
, טור הפורייה שם מתכנס לממוצע 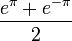
- כלומר, אם נציב
 נקבל:
נקבל:
- נפשט:
הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל
תנאי להתכנסות במ"ש של טור פורייה
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) המקיימת
המקיימת 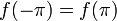 , כך ש
, כך ש 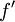 רציפה למקוטעין.
רציפה למקוטעין. - אזי טור הפורייה של
 מתכנס אליה במ"ש בכל הממשיים.
מתכנס אליה במ"ש בכל הממשיים.
- לפי משפט דיריכלה ידוע כי טור הפורייה של ההמשך המחזורי של f מתכנס אליה בכל נקודה.
- נסמן את טור הפורייה ב
- ברור כי
- לפי מבחן ה-M של ויירשטראס, מספיק להוכיח שטור המספרים מימין מתכנס על מנת להסיק שטור הפורייה מתכנס במ"ש.
- נסמן את מקדמי פורייה של הנגזרת ב
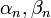 .
. - כבר חישבנו ש:
- לכן ביחד נקבל כי
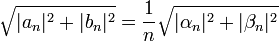
- לפי אי שיוויון קושי שוורץ, נקבל כי לכל n מתקיים:
- לפי אי שיוויון בסל, אנו יודעים כי הטור
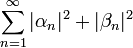 מתכנס, כיוון שמדובר במקדמי פורייה של
מתכנס, כיוון שמדובר במקדמי פורייה של 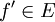 .
.
- (זכרו שמותר להניח כי
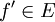 על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
- (זכרו שמותר להניח כי
- לכן
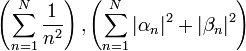 חסומות כסדרות סכומים חלקיים של טורים מתכנסים.
חסומות כסדרות סכומים חלקיים של טורים מתכנסים. - לכן סה"כ
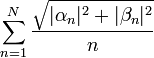 חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
- סה"כ קיבלנו כי
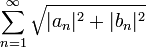 מתכנס.
מתכנס. - לכן בוודאי גם הטורים הקטנים יותר
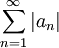 ו
ו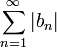 מתכנסים, כפי שרצינו.
מתכנסים, כפי שרצינו.
שיוויון פרסבל
- נביט במערכת האורתונורמלית
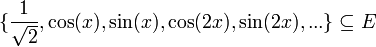
- ידוע לנו כי
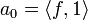 , ולכן
, ולכן 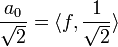
- תהי
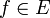 . לפי אי שיוויון בסל ידוע לנו כי:
. לפי אי שיוויון בסל ידוע לנו כי:
- משפט שיוויון פרסבל אומר שבעצם מתקיים:
הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש
- תהי
 רציפה בקטע
רציפה בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) המקיימת
המקיימת 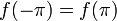 .
.
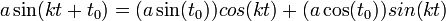
![\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]](/images/math/2/5/f/25f8d4d6c77a138100c89a987596ad1a.png)
![\cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right]](/images/math/f/4/9/f49ffa386014bd9ab57625ca1919dc7d.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1](/images/math/7/9/b/79b96630be4b13a139e89a28e5c3417b.png)
![\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1](/images/math/2/7/b/27bf3f269b2c1bad9a888e32febb6afb.png)
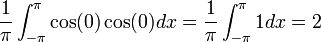
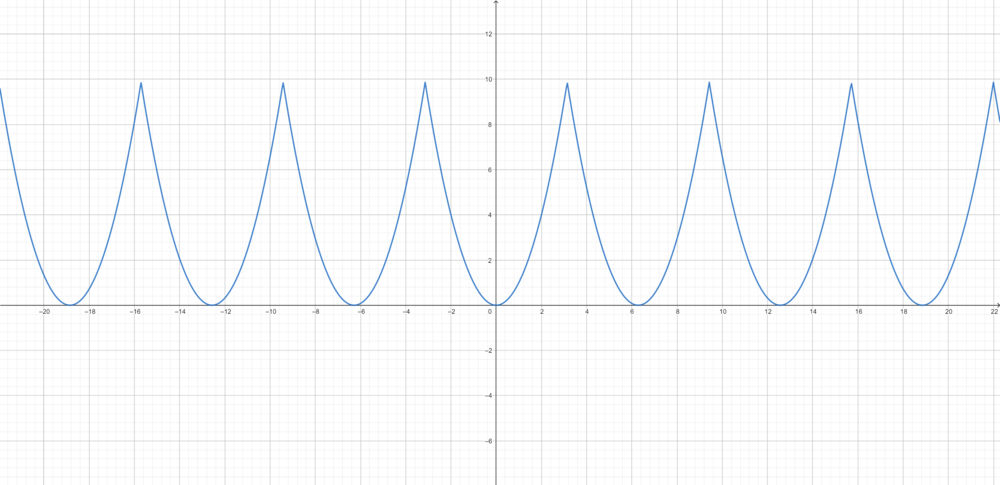
![a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3}](/images/math/6/6/f/66f8ca0042ee471a64c81bf7579cf761.png)
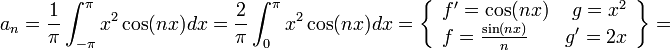
![=\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx=
\left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}=](/images/math/5/1/5/515fbb2ba109a06847f638fe4e5c9362.png)
![- \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2}](/images/math/9/6/2/9628cd82e657ebc65624a51d3a39dcb9.png)
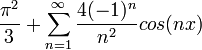
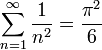
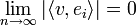
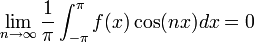
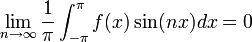
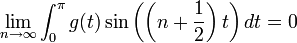
![\int_0^\pi \cos(kt)dt = \left[\frac{\sin(kt)}{k}\right]_0^\pi = 0](/images/math/c/e/c/ceca17ddf194fb7529f19b1be4606a29.png)
![\frac{1}{\pi}\int_0^\pi D_n(t)dt = \frac{1}{\pi}\int_0^\pi \left[\frac{1}{2} + \cos(t) + \cos(2t)+...+\cos(nt)\right]dt = \frac{1}{\pi}\int_0^\pi \frac{1}{2}dt = \frac{1}{2}](/images/math/d/e/4/de4fc431e4665baa4968ff0b9dc3ad7b.png)
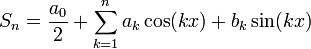
![S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)=](/images/math/9/5/3/95388d9b466e3dbd694aa9869a5afd44.png)
![= \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt=](/images/math/e/a/b/eabf1736c44842010763f0329c0ffc26.png)
![=\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt](/images/math/a/a/6/aa6a06b8a5efdbd5d653eaadfefaf68a.png)
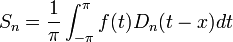
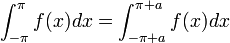
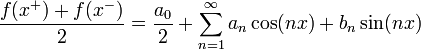
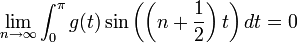
![0=\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]\frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}dt=
\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]D_n(t)dt](/images/math/2/5/0/25079825d14e4fc51335965cdd7ecfdc.png)
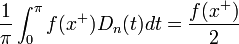
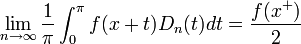
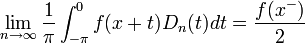
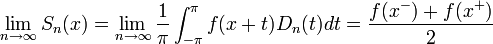
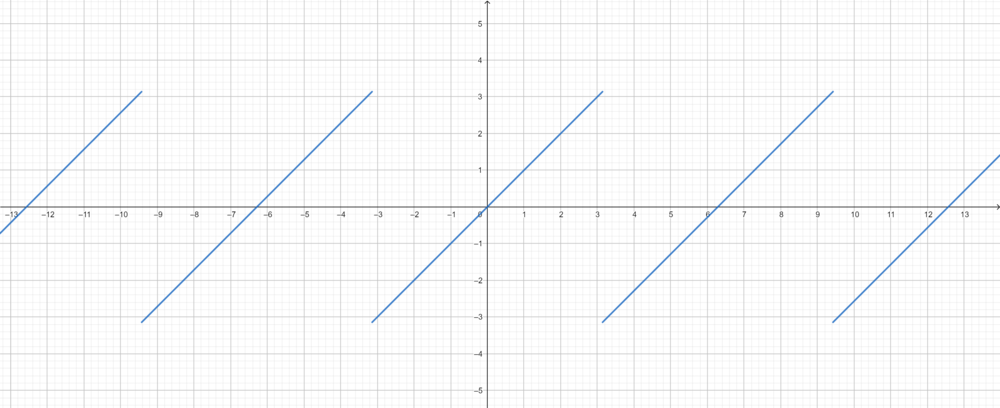
![b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx =
-\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n}](/images/math/9/0/a/90a2ffb7c966e5459fa89d00c8ff7500.png)
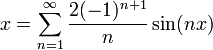
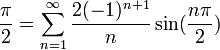
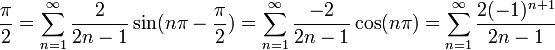
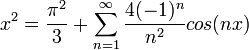
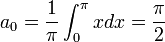
![a_n = \frac{1}{\pi}\int_0^\pi x\cos(nx)dx = \frac{1}{n\pi}\left[x\sin(nx)\right]_0^\pi - \frac{1}{n\pi}\int_0^\pi \sin(nx)dx = \frac{1}{n^2\pi}\left[\cos(nx)\right]_0^\pi=
\frac{(-1)^n-1}{\pi n^2}](/images/math/f/9/c/f9c400eb7eee75c918584f6338d9afa0.png)
![b_n = \frac{1}{\pi}\int_0^\pi x\sin(nx)dx = \frac{-1}{n\pi}\left[x\cos(nx)\right]_0^\pi + \frac{1}{n\pi}\int_0^\pi \cos(nx)dx = \frac{(-1)^{n+1}}{n}](/images/math/4/8/1/481014b617b9eec391447cfa2a17f5f3.png)
![h(x) = \frac{\pi}{4} + \sum_{n=1}^\infty \left[\frac{(-1)^n-1}{\pi n^2}\cos(nx) + \frac{(-1)^{n+1}}{n}\sin(nx)\right]](/images/math/1/4/3/143130c2a183c3e0b99dd1d856502de9.png)
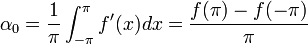
![\alpha_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\cos(nx)dx = \frac{1}{\pi}\left[f(x)\cos(nx)\right]_{-\pi}^\pi +\frac{n}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx =
\frac{(-1)^n\left(f(\pi)-f(-\pi)\right)}{\pi}+n\cdot b_n = (-1)^n\alpha_0+nb_n](/images/math/e/9/b/e9b5cde5f0ea97cd0e133da365d76f3a.png)
![\beta_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\sin(nx)dx = \frac{1}{\pi}\left[f(x)\sin(nx)\right]_{-\pi}^\pi -\frac{n}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = -n\cdot a_n](/images/math/f/4/1/f4193cb204160349b34349a553bbc996.png)