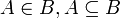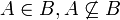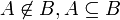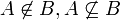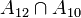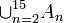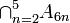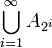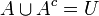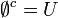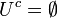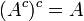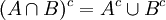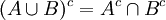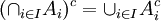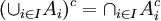הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1"
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
||
| שורה 240: | שורה 240: | ||
בכיוון שני: יהא <math>x\in B^c</math> אזי <math>x\notin B</math> לכן לפי נתון <math>x\notin A</math> לכן <math>x\in A^c</math>. | בכיוון שני: יהא <math>x\in B^c</math> אזי <math>x\notin B</math> לכן לפי נתון <math>x\notin A</math> לכן <math>x\in A^c</math>. | ||
| + | |||
| + | ===== תרגיל ===== | ||
| + | |||
| + | נגדיר <math>\forall n\in \mathbb{N}\cup \{0\} \; A_n:=(n,n+1) \cup (-n-1,-n)</math> אזי | ||
| + | |||
| + | א. <math>\bigcup _{n\in \mathbb{N}} A_n = \mathbb{R}\smallsetminus \mathbb{Z} </math> | ||
| + | |||
| + | ב. <math>\bigcap _{n\in \mathbb{N}} A_n = \varnothing </math> | ||
| + | |||
| + | ג. נגדיר <math>B_n=\mathbb{R}\smallsetminus A_n</math>. חשבו את <math>\bigcap_{n\in \mathbb{N}} B_n</math> | ||
| + | |||
| + | הוכחה: | ||
| + | |||
| + | א. ע"י הכלה דו כיוונית. | ||
| + | |||
| + | ב. מספיק להראות <math>A_1\cap A_2=\phi</math>. | ||
| + | |||
| + | ג. נתייחס ל-<math>\mathbb{R}</math> כקבוצה האוניברסלית לדיוננו. לפי דה-מורגן נקבל:<math>\bigcap_{n\in \mathbb{N}} B_n=\bigcap_{n\in \mathbb{N}} A_n^c=(\bigcup_{n\in \mathbb{N}} A_n)^c=(\mathbb{Z}^c)^c=\mathbb{Z}</math>. | ||
=== קבוצת החזקה === | === קבוצת החזקה === | ||
גרסה מ־19:19, 9 ביולי 2019
קישורים
מידע רב חופף בין הקורס שלנו לקורס תורת הקבוצות, ניתן להעזר לכן בקורס תורת הקבוצות בויקיפדיה
קבוצות
ההגדרה האינטואיטיבית לקבוצה הינה "אוסף של איברים". ההגדרה הזו מובילה לסתירות לוגיות כגון "פרדוקס ראסל". נביט בקבוצה הבאה:
- X=אוסף כל הקבוצות שאינן שייכות לעצמן
אם X שייכת לקבוצה הזו, אזי היא אינה שייכת לקבוצה. אולם, אם היא אינה שייכת לקבוצה אזי היא כן שייכת לקבוצה.
סתירה אינה מקובלת במחוזות המתמטיקאים, ולכן הגדירו את "תורת הקבוצות האקסיומטית" העוקפת בעייה זו. ניתן לקרוא יותר על נושא זה בקישור לעיל, עבורנו מספיקה ההגדרה האינטואיטיבית.
אם כן, נחזור להגדרתנו הנאיבית; קבוצה הינה אוסף של איברים שונים. בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות:
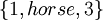 ,
, 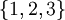 ו
ו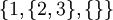
איבר השייך לקבוצה אנו מסמנים בסימן 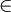 . למשל
. למשל 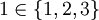 , ואילו
, ואילו 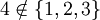 . שימו לב שגם
. שימו לב שגם 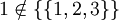 שכן האיבר היחיד בקבוצה זו הינה הקבוצה
שכן האיבר היחיד בקבוצה זו הינה הקבוצה 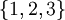 .
.
- אומרים שקבוצה A מוכלת בקבוצה B (מסומן
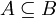 ) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים
) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים 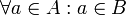 .
.
- דוגמא:
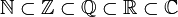 כאשר
כאשר
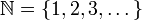 המספרים הטבעיים
המספרים הטבעיים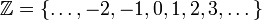 המספרים השלמים
המספרים השלמים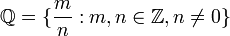 המספרים הרציונאלים (שברים)
המספרים הרציונאלים (שברים)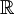 המספרים הממשיים ("כל המספרים" על הישר)
המספרים הממשיים ("כל המספרים" על הישר)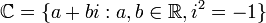 המספרים המרוכבים
המספרים המרוכבים
תרגיל
מצאו קבוצות A,B כך ש:
תרגיל
נתון 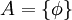 ונתון
ונתון 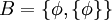 . סמן את הביטויים הנכונים:
. סמן את הביטויים הנכונים:
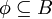 (כן)
(כן)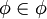 (לא)
(לא)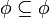 (כן)
(כן)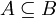 (כן)
(כן)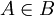 (כן)
(כן)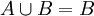 (כן)
(כן)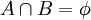 (לא)
(לא)
תרגיל
נתונות 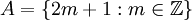 , ו
, ו 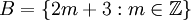 . הוכח שA=B.
. הוכח שA=B.
פתרון
נוכיח הכלה דו כיוונית. נניח 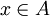 לכן קיים מספר שלם m כך ש
לכן קיים מספר שלם m כך ש 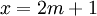 . קל לראות שמתקיים
. קל לראות שמתקיים 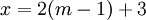 אבל אז מכיוון ש m-1 הינו מספר שלם מתקיים
אבל אז מכיוון ש m-1 הינו מספר שלם מתקיים 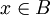 כפי שרצינו.
כפי שרצינו.
ההכלה בכיוון ההפוך דומה.
תרגיל
הוכיחו כי 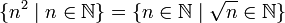
פעולות על קבוצות
- חיתוך של שתי קבוצות A ו B הינו אוסף האיברים השייכים גם לA וגם לB (מסומן
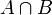 ). מתקיים ש
). מתקיים ש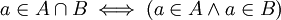 .
.
- איחוד של שתי קבוצות A ו B הינו אוסף האיברים השייכים לA או לB (מסומן
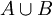 ). מתקיים ש
). מתקיים ש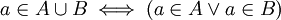 .
.
- קבוצות הן שוות אם הן מכילות את אותם האיברים. הדרך הנפוצה להוכיח שיוויון הינה הכלה דו כיוונית: A=B אם ורק אם
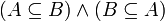 .
.
- A הפרש B הינה הקבוצה המכילה את כל האיברים בA שאינם בB (מסומן A\B). מתקיים ש
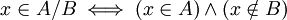 .
.
- ההפרש הסימטרי בין שתי קבוצות A וB הוא אוסף האיברים הנמצאים באחת הקבוצות אך לא בחיתוך (מסומן
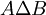 ). מתקיים ש
). מתקיים ש 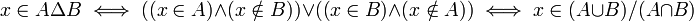
דוגמא:
יהיו 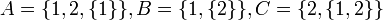 קבוצות.
קבוצות.
אזי:
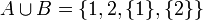
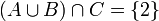
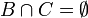

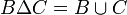
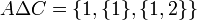
תכונות האיחוד והחיתוך (דומה לכפל וחיבור)
- אסוציאטיביות:
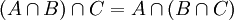 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - חילוף:
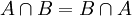 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - דיסטריביוטיביות:
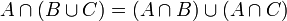 , וגם
, וגם 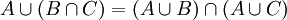
תרגיל
הוכח כי 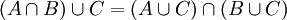 . במילים: האיברים שהם (גם בA וגם בB) או בC הם בדיוק האיברים ב(A או C) וגם ב(B או C)
. במילים: האיברים שהם (גם בA וגם בB) או בC הם בדיוק האיברים ב(A או C) וגם ב(B או C)
פתרון
נראה שקילות בין התנאים של איבר להיות באחת הקבוצות.
![x\in (A\cap B)\cup C \iff [x\in (A\cap B)] \or [x\in C] \iff [x\in A \and x\in B] \or [x\in C]](/images/math/5/a/4/5a46220a7b2be5a95beb3cbab300380a.png)
כעת, מתוך הטאוטולוגיה 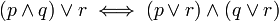 קל להשיג את השקילות למה שצריך.
(הערה: ניתן להשתכנע בקלות בטאוטולוגיה באופן הבא: אם r=1 אזי נשאר עם הטאוטולוגיה
קל להשיג את השקילות למה שצריך.
(הערה: ניתן להשתכנע בקלות בטאוטולוגיה באופן הבא: אם r=1 אזי נשאר עם הטאוטולוגיה
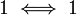 אם r=0 אזי נשאר עם הטאוטולוגיה
אם r=0 אזי נשאר עם הטאוטולוגיה
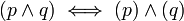 )
)
תרגיל
הוכח כי:
א. הקבוצה הריקה 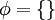 מוכלת בכל קבוצה A
מוכלת בכל קבוצה A
ב. 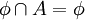
ג. 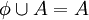
פתרון
א. יש להוכיח את הפסוק הבא: 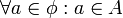 . אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
הערה: שימו לב שעל מנת להוכיח שקבוצה A אינה מוכלת בקבוצה B, יש להראות כי קיים איבר בA שאינו שייך לB. אם היינו משתמשים בפסוק "כל האיברים בA אינם בB" היינו מקבלים שהקבוצה הריקה לא מוכלת בכל קבוצה, וגם אינה מוכלת בכל קבוצה.
. אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
הערה: שימו לב שעל מנת להוכיח שקבוצה A אינה מוכלת בקבוצה B, יש להראות כי קיים איבר בA שאינו שייך לB. אם היינו משתמשים בפסוק "כל האיברים בA אינם בB" היינו מקבלים שהקבוצה הריקה לא מוכלת בכל קבוצה, וגם אינה מוכלת בכל קבוצה.
ב. 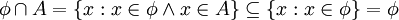
ג. 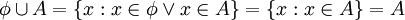
תרגיל
הוכח כי 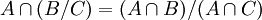
פתרו:
דרך גרירות לוגיות:
![x\in A\cap (B/C)\iff (x\in A) \and [(x\in B) \and (x\notin C)]\iff [(x\in A) \and (x\in B) \and (x\notin C)] \or [(x\in A) \and (x\in B) \and (x\notin A)]](/images/math/5/f/c/5fcc49e93a43d72a27f2ce5b2d9a7dc2.png)
בצד הימני הוספנו סתירה בעזרת הקשר "או" ולכן נשארנו עם ביטוי שקול. כעת נשתמש בחוק הפילוג של הלוגיקה:
![\iff [(x\in A) \and (x\in B)]\and [(x\notin C)\or(x\notin A)]\iff [(x\in A) \and (x\in B)]\and \neg [(x\in C)\and(x\in A)]](/images/math/e/f/8/ef804662c2efab381fbe719261ae3d1f.png)
וזה בדיוק מה שרצינו.
דרך הכלה דו כיוונית:
(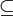 ) נניח
) נניח 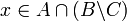 אזי
אזי
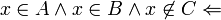
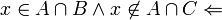
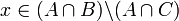
(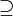 ) נניח
) נניח 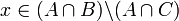 אזי
אזי
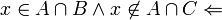
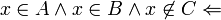 (כי אם
(כי אם 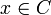 אזי
אזי 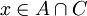 סתירה)
סתירה)
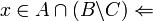
הכללה לאיחודים וחיתוכים כל שהם
מוטיבציה: הגדרנו את החיתוך והאיחוד עבור שתי קבוצות. לעיתים נרצה לחתוך או לאחד יותר קבוצות, לדוגמא נרצה לדבר על חיתוכן של 17 הקבוצות 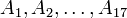 . מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום
. מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום 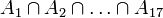 , וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא:
, וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא: 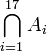 . לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
. לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
הגדרה:
יהיו 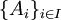 אוסף קבוצות כאשר
אוסף קבוצות כאשר 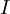 הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
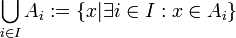
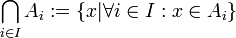 . כאן יש להניח שקבוצת האינדקסים
. כאן יש להניח שקבוצת האינדקסים 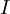 לא ריקה.
לא ריקה.
דוגמא:
נגדיר ![\forall n\in \mathbb{N} \; A_n:=[n,n+1]](/images/math/b/e/6/be669fb7637e3c1c6e6bd1431436da46.png) אזי
אזי
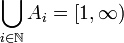
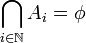
תרגיל
לכל n>1 טבעי נגדיר 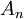 להיות קבוצת כל הראשוניים המחלקים את n.
להיות קבוצת כל הראשוניים המחלקים את n.
חשבו את
תרגיל (הכללת פילוג)
יהיו 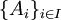 אוסף קבוצות, B קבוצה. הוכיחו כי
אוסף קבוצות, B קבוצה. הוכיחו כי
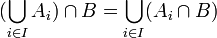
פתרון:
יהא 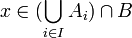 אזי
אזי 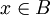 וגם
וגם 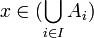 לכן
לכן 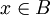 וגם
וגם 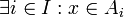 ולכן
ולכן 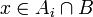 ומכאן ש
ומכאן ש 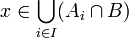
בכיוון שני: יהא 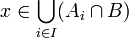 ולכן
ולכן 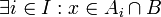 לכן
לכן 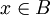 וגם
וגם 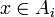 לכן
לכן 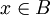 וגם
וגם 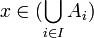 ולכן
ולכן 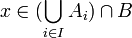
משלים
הגדרה: תהי קבוצה U, ונביט בתת קבוצה שלה A. ניתן להגדיר את המשלים של A כאוסף האיברים בU שאינם בA (כלומר ההפרש 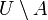 ), מסומן
), מסומן 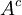 . לא ניתן לדבר על משלים אוניברסאלי ללא U מכיוון שאין קבוצה המכילה את כל הדברים בעולם (אחרת נגיע לסתירות כמו פרדוקס ראסל).
. לא ניתן לדבר על משלים אוניברסאלי ללא U מכיוון שאין קבוצה המכילה את כל הדברים בעולם (אחרת נגיע לסתירות כמו פרדוקס ראסל).
תכונות בסיסיות:
על המשלימים מתקיימים חוקי דה מורגן (הנובעים ישירות מחוקי דה מורגן בלוגיקה):
הערה: באופן כללי מתקיים
תרגיל
הוכיחו כי 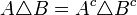 .
.
פתרון:
נשתמש בהצגת ההפרש הסימטרי כאיחוד ההפרשים:
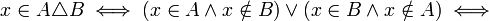
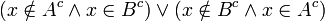 ומחילופיות "וגם" ו"או":
ומחילופיות "וגם" ו"או":
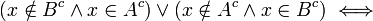
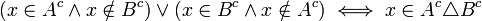
תרגיל
יהיו A,B ת"ק של U אזי 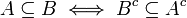
פתרון: בכיוון אחד- יהא 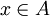 אזי
אזי 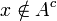 לכן לפי נתון
לכן לפי נתון 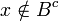 לכן
לכן 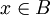 .
.
בכיוון שני: יהא 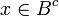 אזי
אזי 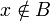 לכן לפי נתון
לכן לפי נתון 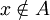 לכן
לכן 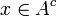 .
.
תרגיל
נגדיר 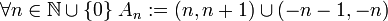 אזי
אזי
א. 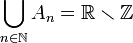
ב. 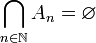
ג. נגדיר 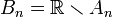 . חשבו את
. חשבו את 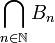
הוכחה:
א. ע"י הכלה דו כיוונית.
ב. מספיק להראות 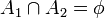 .
.
ג. נתייחס ל-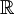 כקבוצה האוניברסלית לדיוננו. לפי דה-מורגן נקבל:
כקבוצה האוניברסלית לדיוננו. לפי דה-מורגן נקבל: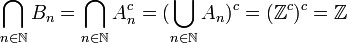 .
.
קבוצת החזקה
הגדרה: תהי קבוצה A. נגדיר את קבוצת החזקה של A בתור אוסף כל תתי הקבוצות של A. מסומן 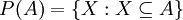
דוגמא:
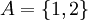 אזי
אזי 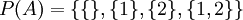 .
.
האם אתם יכולים למנות כמה איברים יש בקבוצת החזקה?
תרגיל ממבחן
יהיו A,B,C קבוצות. הוכיחו/הפריכו:
א. אם 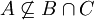 אזי
אזי 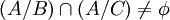
ב. אם 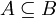 אזי
אזי 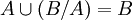
ג. אם 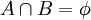 אזי
אזי 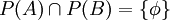
פתרון
א. הפרכה: 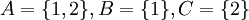 . אזי ברור שA איננה מוכלת בחיתוך של B וC אבל
. אזי ברור שA איננה מוכלת בחיתוך של B וC אבל 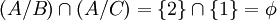
ב. נתון שלכל  מתקיים
מתקיים 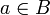 . אזי
. אזי ![x\in [A\cup(B/A)] \iff (x\in A) \or [(x\in B)\and (x\notin A)] \iff [(x\in A) \or (x\in B)] \and [(x \in A)\or (x\notin A)]](/images/math/f/8/a/f8a74cc645180bad23b7a6f990e383e0.png)
כעת, הצד הימני הוא טאוטולוגיה וניתן להסיר אותו. מכיוון שנתון  ניתן להסיק בקלות ש
ניתן להסיק בקלות ש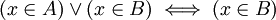 כפי שרצינו.
כפי שרצינו.
דרך נוספת: נגדיר את B להיות הקבוצה האוניברסאלית 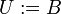 ואז צריך להוכיח כי
ואז צריך להוכיח כי
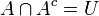 וזה אכן נכון!
וזה אכן נכון!
ג. נניח בשלילה ש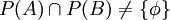 . מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה
. מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה 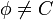 השייכת לחיתוך
השייכת לחיתוך 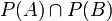 . קבוצות החזקה הן אוסף תתי הקבוצות, ולכן
. קבוצות החזקה הן אוסף תתי הקבוצות, ולכן 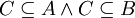 . מכיוון שC אינה ריקה קיים בה איבר
. מכיוון שC אינה ריקה קיים בה איבר 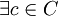 וקל מאד לראות ש
וקל מאד לראות ש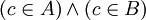 ולכן c מוכל בחיתוך בסתירה לכך שהחיתוך ריק.
ולכן c מוכל בחיתוך בסתירה לכך שהחיתוך ריק.