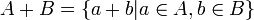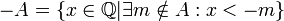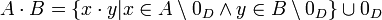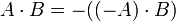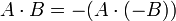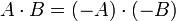הבדלים בין גרסאות בדף "חתכי דדקינד"
מתוך Math-Wiki
(←כפל חתכי דדקינד) |
(←כפל חתכי דדקינד) |
||
| שורה 122: | שורה 122: | ||
**<math>A\cdot B = (-A)\cdot (-B)</math> | **<math>A\cdot B = (-A)\cdot (-B)</math> | ||
| + | ===הוכחה שהמכפלה נותנת חתך דדקינד=== | ||
| + | *יהיו שני חתכי דדקינד '''אי שליליים''' <math>0_D\leq A,B</math> | ||
| + | |||
| + | |||
| + | *ברור שהמכפלה לא ריקה כיוון ש <math>0_D\subseteq A\cdot B</math> | ||
| + | |||
| + | |||
| + | *כיוון שA,B חתכי דדקינד מדובר בקבוצות חסומות, אז קיימים חסמי מלעיל <math>m_A,m_B</math> בהתאמה. | ||
| + | *לכל <math>xy\in AB</math> מתקיים כי <math>x<m_A,y<m_B</math> ולכן <math>xy<m_A\cdot m_B</math>. זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים. | ||
| + | |||
| + | |||
| + | *אם <math>t\in AB</math> צ"ל כי <math>t</math> אינו חסם מלעיל של <math>AB</math>. | ||
| + | *אם <math>t\leq 0</math> ברור שאינו חסם מלעיל של <math>AB</math> כיוון שיש בקבוצה מספרים חיוביים. | ||
| + | *לכן <math>t=xy\in AB</math>. | ||
| + | *כיוון ש<math>x</math> אינו חסם מלעיל של <math>A</math> קיים <math>x<z\in A</math> ולכן <math>xy<zy\in A</math> בסתירה. | ||
| + | |||
| + | *אם <math>t\not\in AB</math> צ"ל כי <math>t</math> חסם מלעיל. | ||
===חתך היחידה=== | ===חתך היחידה=== | ||
גרסה מ־15:39, 26 במרץ 2022
תוכן עניינים
הקדמה
- אנחנו מעוניינים שבמערכת המספרים שלנו יהיה פתרון למשוואה
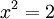 (שורש שתיים).
(שורש שתיים).
- הרי אחרת, מה המרחק מהנקודה
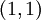 לראשית הצירים
לראשית הצירים 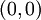 ?
?
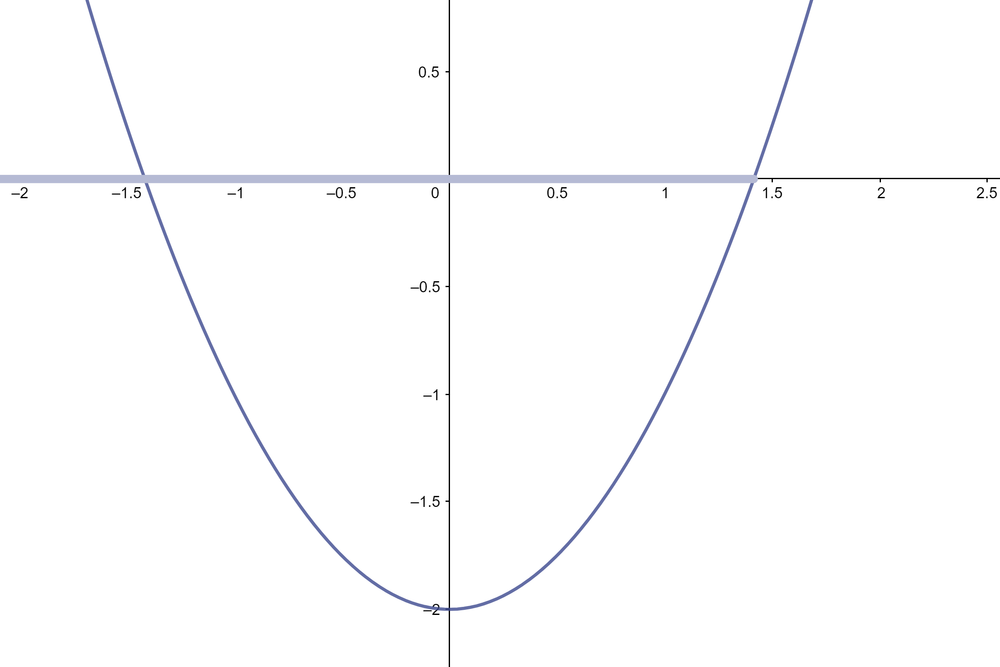
- האם ייתכן שהפרבולה
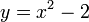 עולה מהנקודה
עולה מהנקודה 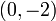 אל הנקודה
אל הנקודה 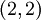 בלי לחתוך את ציר האיקס?
בלי לחתוך את ציר האיקס?
- כיוון שאין פתרון למשוואה זו בשדה הרציונאליים, אנחנו רוצים לבנות את שדה הממשיים.
- כיצד ניתן לתאר את נקודת החיתוך החיובית של הפרבולה
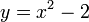 עם ציר האיקס באמצעות המספרים הרציונאליים אם כך?
עם ציר האיקס באמצעות המספרים הרציונאליים אם כך?
(נבנה באמצעות גאוגברה.)
- ובכן, ניתן לומר שציר המספרים מתחלק לשניים - לפני שורש שתיים ואחרי שורש שתיים.
- כלומר, אולי אנחנו יכולים לייצג את נקודת החיתוך על ידי אוסף הנקודות שקטנות ממנה
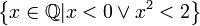 , זו הקרן באיור.
, זו הקרן באיור.
- הרעיון הזה של חיתוך ציר הרציונאליים סביב נקודה בלתי קיימת הוליד את חתכי דדקינד.
חתכי דדקינד
- הגדרה: חתך דדקינד הוא קבוצה
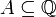 המקיימת:
המקיימת:
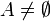
 חסומה מלעיל.
חסומה מלעיל.- לכל
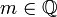 מתקיים כי
מתקיים כי 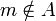 אם ורק אם
אם ורק אם 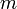 חסם מלעיל של
חסם מלעיל של 
- הערות ותזכורות:
- חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה.
- בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה. זה משול לחצי האבוקדו ללא הגרעין.
- בחתך המייצג מספר שאינו רציונאלי, כמו שורש שתיים, גם במשלים של החתך אין מספר קטן ביותר, זה משול לשני חצאי אבוקדו ללא גרעין כלל.
- אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל.
- הקרן באיור לעיל היא חתך דדקינד שתפקידו להגדיר את שורש שתיים.
- כיצד ניתן להתייחס לקבוצות כאלה בתור מספרים?
- עלינו להגיד פעולות בין חתכי דדקינד ולהוכיח שמדובר בשדה.
- כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר.
חיבור חתכי דדקינד
- יהיו שתי חתכים
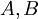 , נגדיר את החיבור:
, נגדיר את החיבור:
- החיבור הוא חתך דדקינד בעצמו:
- כיוון שA,B אינן ריקות גם A+B אינה ריקה.
- סכום חסמי מלעיל של A וB חוסם את A+B.
- יהי
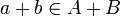 , כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים
, כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים 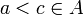 וכן
וכן 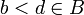 ולכן
ולכן 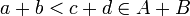 ו
ו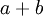 אינו חסם מלעיל של
אינו חסם מלעיל של 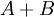
- יהי
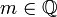 שאינו חסם מלעיל של
שאינו חסם מלעיל של 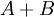 , לכן קיימים
, לכן קיימים 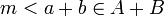 . כעת
. כעת 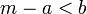 כלומר
כלומר 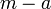 אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ
אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ 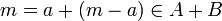 .
.
חתך האפס
- נגדיר את חתך האפס, בהמשך נוכיח שהוא נייטרלי לחיבור.
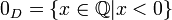
נגדי
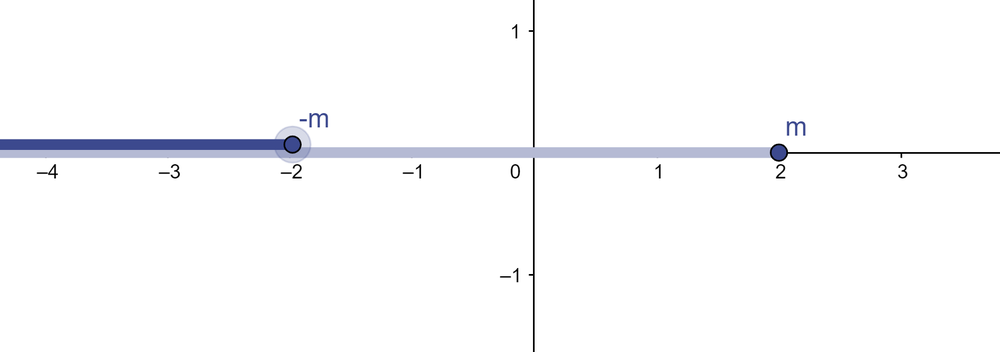
- יהי חתך A, נגדיר את הנגדי:
- לדוגמא
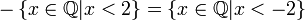
- הנגדי הוא חתך דדקינד בעצמו:
- הנגדי לא ריק:
- כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן
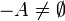
- כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן
- הנגדי חסום מלעיל:
- יהי
 לכן לכל
לכן לכל 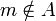 מתקיים כי
מתקיים כי 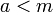 ולכן
ולכן 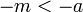
- לכל
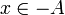 קיים
קיים 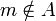 כך ש
כך ש 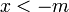 ולכן
ולכן 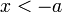
- בעצם הנגדי של כל איבר בA הוא חסם מלעיל של
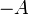 .
.
- יהי
- כל איבר בנגדי אינו חסם מלעיל:
- לכל איבר בנגדי
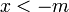 לכן אמצע הקטע בין
לכן אמצע הקטע בין 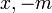 גדול מ
גדול מ וקטן מ
וקטן מ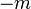 ולכן שייך לנגדי
ולכן שייך לנגדי 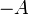 ולכן
ולכן  אינו חסם מלעיל.
אינו חסם מלעיל.
- לכל איבר בנגדי
- אם איבר אינו חסם מלעיל, הוא שייך לנגדי:
- נניח
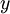 אינו חסם מלעיל של
אינו חסם מלעיל של 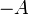 לכן קיים
לכן קיים 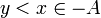 ולכן קיים
ולכן קיים 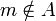 כך ש
כך ש 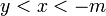 ולכן
ולכן 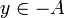
- נניח
- הנגדי לא ריק:
יחס סדר
- יחס ההכלה הוא יחס סדר לינארי (מלא) על קבוצת חתכי דדקינד
- הוכחה:
- יהיו שני חתכים A,B.
- אם קיים
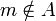 חסם מלעיל של A כך ש
חסם מלעיל של A כך ש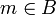 אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר
אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר 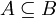
- אחרת, לכל
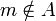 מתקיים כי
מתקיים כי 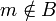 . כלומר
. כלומר 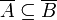 ולכן
ולכן 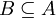
- נגדיר את החתכים החיוביים להיות כל החתכים A כך ש
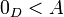 ונגדיר את החתכים השליליים על ידי
ונגדיר את החתכים השליליים על ידי 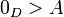
- טענה:
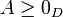 אם ורק אם
אם ורק אם 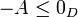
- הוכחה:
- ראשית נניח כי
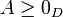
- כלומר בעצם
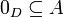 ולכן לכל חסם מלעיל
ולכן לכל חסם מלעיל 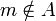 מתקיים כי
מתקיים כי 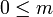 .
. - לכן לכל
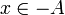 מתקיים כי
מתקיים כי 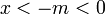
- כלומר כל האיברים ב
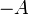 שליליים, ולכן
שליליים, ולכן 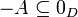 כלומר
כלומר 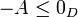
- כלומר בעצם
- בכיוון ההפוך, נניח כי
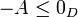
- לכן כל האיברים ב
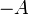 שליליים.
שליליים. - אם קיים
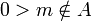 אזי
אזי 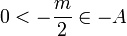 בסתירה.
בסתירה.
- לכן כל האיברים ב
- לכן כל המספרים השליליים שייכים לA, כלומר
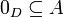 ולכן
ולכן 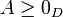
- ראשית נניח כי
כפל חתכי דדקינד
- יהיו שני חתכי דדקינד אי שליליים
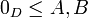 , נגדיר את הכפל:
, נגדיר את הכפל:
- אם A שלילי, וB אי שלילי, נגדיר:
- אם A אי שלילי, וB שלילי, נגדיר:
- אם A,B שליליים נגדיר:
הוכחה שהמכפלה נותנת חתך דדקינד
- יהיו שני חתכי דדקינד אי שליליים
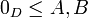
- ברור שהמכפלה לא ריקה כיוון ש
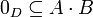
- כיוון שA,B חתכי דדקינד מדובר בקבוצות חסומות, אז קיימים חסמי מלעיל
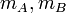 בהתאמה.
בהתאמה. - לכל
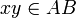 מתקיים כי
מתקיים כי 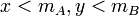 ולכן
ולכן 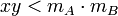 . זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים.
. זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים.
- אם
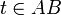 צ"ל כי
צ"ל כי 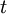 אינו חסם מלעיל של
אינו חסם מלעיל של 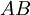 .
. - אם
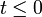 ברור שאינו חסם מלעיל של
ברור שאינו חסם מלעיל של 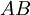 כיוון שיש בקבוצה מספרים חיוביים.
כיוון שיש בקבוצה מספרים חיוביים. - לכן
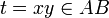 .
. - כיוון ש
 אינו חסם מלעיל של
אינו חסם מלעיל של  קיים
קיים 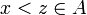 ולכן
ולכן 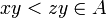 בסתירה.
בסתירה.
- אם
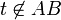 צ"ל כי
צ"ל כי 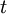 חסם מלעיל.
חסם מלעיל.
חתך היחידה
- נגדיר את חתך היחידה, בהמשך נוכיח שהוא נייטרלי לכפל.
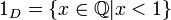
הופכי
- אם A חיובי נגדיר את ההופכי שלו להיות
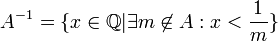
- אם A שלילי נגדיר את ההופכי שלו להיות
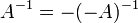
שדה הממשיים
הגדרת המספרים הממשיים
- הגדרה:
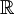 הוא קבוצת כל חתכי דדקינד.
הוא קבוצת כל חתכי דדקינד.
- נוכיח שמדובר בשדה סדור ביחס לפעולות החיבור והכפל ויחס הסדר שהגדרנו לעיל, ולאחר מכן נתאר את הייצוג העשרוני של המספרים הממשיים.
שלמות הממשיים
- תהי
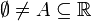 קבוצה לא ריקה של מספרים ממשיים, וחסומה מלעיל (כלומר קיים
קבוצה לא ריקה של מספרים ממשיים, וחסומה מלעיל (כלומר קיים 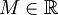 כך ש
כך ש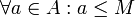 . אזי קיים ל
. אזי קיים ל חסם עליון ממשי.
חסם עליון ממשי.
הוכחה
- נסמן ב
 את האיחוד הכללי של כל חתכי הדדקינד ששייכים ל
את האיחוד הכללי של כל חתכי הדדקינד ששייכים ל , כלומר
, כלומר 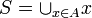
- נוכיח כי האיחוד הכללי של כל חתכי הדדקינד הוא גם חתך דדקינד.
 אינה ריקה
אינה ריקה
 אינה ריקה, ולכן קיים
אינה ריקה, ולכן קיים 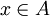 .
. - כיוון ש
 חתך דדקינד הוא אינו ריק.
חתך דדקינד הוא אינו ריק. 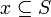 ולכן
ולכן  אינה ריקה
אינה ריקה
 חסומה:
חסומה:
- כיוון ש
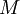 חסם מלעיל של
חסם מלעיל של  לכל
לכל 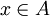 מתקיים כי
מתקיים כי 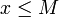
- לפי יחס הסדר מתקיים כי
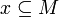 .
. - כיוון שלכל
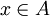 מתקיים כי
מתקיים כי 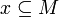 נובע כי גם
נובע כי גם 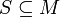 .
. - לכן
 חסומה מלעיל.
חסומה מלעיל.
- כיוון ש
- נוכיח כי
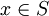 אם ורק אם
אם ורק אם  אינו חסם מלעיל של
אינו חסם מלעיל של 
- אם
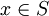 אזי
אזי 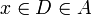
- אם
 חסם מלעיל של
חסם מלעיל של  אזי הוא בפרט חסם מלעיל של
אזי הוא בפרט חסם מלעיל של 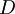 בסתירה.
בסתירה. - מצד שני, אם
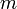 חסם מלעיל של
חסם מלעיל של  הוא בפרט חסם מלעיל של כל איברי
הוא בפרט חסם מלעיל של כל איברי  ולכן אינו שייך לאף אחד מאיברי
ולכן אינו שייך לאף אחד מאיברי  ולכן אינו שייך ל
ולכן אינו שייך ל
- אם
- ברור כי לכל
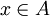 מתקיים כי
מתקיים כי 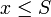 כיוון ש
כיוון ש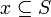 (כל קבוצה מוכלת באיחוד).
(כל קבוצה מוכלת באיחוד).
- נוכיח כי
 הוא החסם העליון של
הוא החסם העליון של  .
. - נב"ש כי קיים
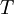 חסם מלעיל של
חסם מלעיל של  כך ש
כך ש 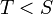 .
. - לכן קיים
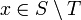 .
. - לכן קיים
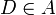 כך ש
כך ש 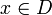 .
. - לכן
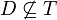 בסתירה לכך ש
בסתירה לכך ש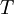 חסם מלעיל של
חסם מלעיל של