משתמש:אור שחף/133 - תרגול/6.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - תרגול
תוכן עניינים
שיטות פרמיטיביות לחישוב שטחים
המטרה: לחשב שטח מתחת לכל עקומה (כמעט).
דוגמה 1
חשב את השטח הכלוא בין ציר ה-x לעקומה במקרים הבאים:
-
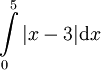
פתרון: נשים לב להגדרת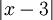 לפיה האינטגרל שווה ל-
לפיה האינטגרל שווה ל-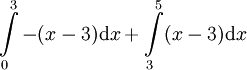 . גרף (1) מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I -
. גרף (1) מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I - 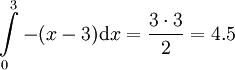 ועבור II -
ועבור II - 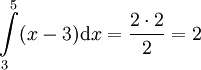 ולכן השטח הכולל הוא 6.5.
ולכן השטח הכולל הוא 6.5. 
הערה: אם התחום היה, למשל,![[4,5]](/images/math/3/0/e/30eeb203d66f0c29522e851b605d8a9e.png) היינו יכולים לחשב לפי שטח טרפז.
היינו יכולים לחשב לפי שטח טרפז. -
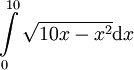 . פתרון: נבדוק מהו גרף הפונקציה. נסמן
. פתרון: נבדוק מהו גרף הפונקציה. נסמן 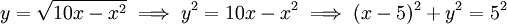 . קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל.
. קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל. 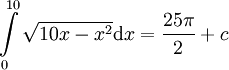

-
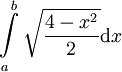 , כאשר a,b הם גבולות העקומה. פתרון: נסמן
, כאשר a,b הם גבולות העקומה. פתרון: נסמן  . זוהי אליפסה שמרכזה ב-
. זוהי אליפסה שמרכזה ב-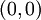 . נסמן
. נסמן 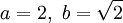 ולפי נוסחה לשטח אליפסה (
ולפי נוסחה לשטח אליפסה (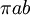 ) נקבל
) נקבל 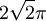 . האינטגרל הוא מחצית השטח, כלומר
. האינטגרל הוא מחצית השטח, כלומר 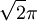 .
. 
האינטגרל הלא מסויים
המטרה: להגדיר אינטגרל דרך פונקציה קדומה: 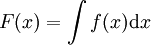 ולכן אפשר להשתמש בכיוון השני של טבלת הגזירה. למשל,
ולכן אפשר להשתמש בכיוון השני של טבלת הגזירה. למשל, 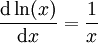 ולכן
ולכן 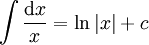
דוגמה 1 (שיטת פירוק)
חשב 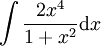 .
.
פתרון
זה שווה ל-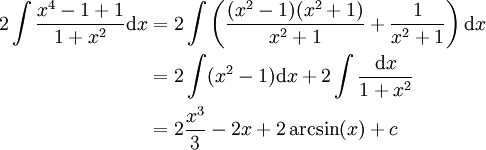

באופן כללי: נבדוק מה מאפס את המונה ומה מאפס את המכנה (במקרה הזה לא מתאפס ב- ). אם מצטמצם ננסה חילוק פולינומים, אחרת נחפס להציג כקבוע ועוד שארית. דוגמה נוספת:
). אם מצטמצם ננסה חילוק פולינומים, אחרת נחפס להציג כקבוע ועוד שארית. דוגמה נוספת: 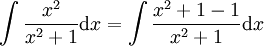 .
.
דוגמה 2
חשב 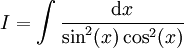 .
.
פתרון
דרך א: מתקיים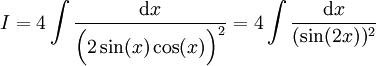 . זהו אינטגרל לא פשוט ולכן ננסה את דרך ב:
. זהו אינטגרל לא פשוט ולכן ננסה את דרך ב: 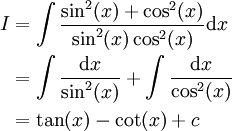

ניתן לבדוק זאת ע"י גזירת הפונקציה הקדומה, אבל כמובן שההוכחה הזו מספיקה.
שיטת ההצבה: 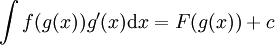
דוגמה 3
חשב 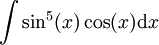 .
.
פתרון
נציב 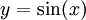 ולכן
ולכן 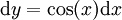 . אזי האינטגרל הוא:
. אזי האינטגרל הוא: 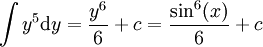 .
. 
אינטגרציה בחלקים: 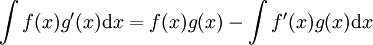 .
.
דוגמה 4
חשב את האינטגרלים הבאים:
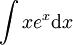
פתרון
לפי אינטגרציה בחלקים, נגדיר
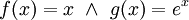 . לכן האינטגרל שווה ל-
. לכן האינטגרל שווה ל-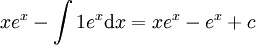 .
. 
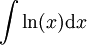
פתרון
נסמן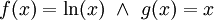 ואז
ואז 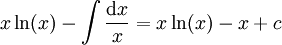 .
. 
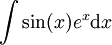
פתרון
מסקנה: במקרה של-f,g יש מספר סופי של נגזרות שונות, נשתמש בשיטה זו.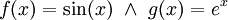 ואז
ואז 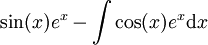 . ולפי אינטגרציה שנייה:
. ולפי אינטגרציה שנייה: 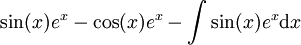 ולכן
ולכן 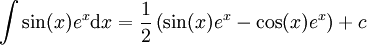 .
. 
דוגמה 5
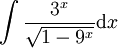 .
.
פתרון
בשיטת ההצבה, 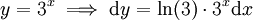 והאינטגרל הנ"ל שווה ל-
והאינטגרל הנ"ל שווה ל-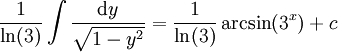 .
. 