משתמש:אור שחף/133 - הרצאה/15.5.11
תוכן עניינים
התכנסות במידה שווה (המשך)
תרגיל ברוח מבחן
נניח ש-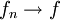 במ"ש על I וש-
במ"ש על I וש-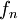 חסומה ב-I לכל n. הוכיחו כי גם f חסומה ב-I והראו ע"י דוגמה שהתוצאה אינה נכונה אם
חסומה ב-I לכל n. הוכיחו כי גם f חסומה ב-I והראו ע"י דוגמה שהתוצאה אינה נכונה אם 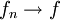 נקודתית ב-I.
נקודתית ב-I.
פתרון
אם 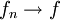 במ"ש ב-I אז נוכל לקחת
במ"ש ב-I אז נוכל לקחת 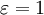 ולכן קיים n מסויים כך שלכל
ולכן קיים n מסויים כך שלכל 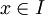 מתקיים
מתקיים 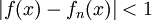 ונובע מאי-שיוויון המשולש כי לכל
ונובע מאי-שיוויון המשולש כי לכל 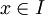 מתקיים
מתקיים 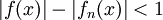 . לכן
. לכן 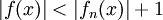 . נתון ש-
. נתון ש-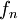 חסומה, נניח
חסומה, נניח 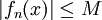 אזי
אזי 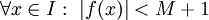 .
. 
לגבי הדוגמה הנגדית, נגדיר 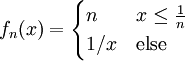 ב-
ב-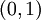 . אזי
. אזי 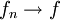 נקודתית וכל
נקודתית וכל 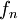 חסומה ע"י n, אלא ש-
חסומה ע"י n, אלא ש-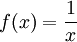 , שבוודאי לא חסומה.
, שבוודאי לא חסומה. 
הגדרה: נתונה סדרת פונקציות 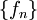 בקטע I. נאמר שהסדרה מקיימת את תנאי קושי במ"ש ב-I אם לכל
בקטע I. נאמר שהסדרה מקיימת את תנאי קושי במ"ש ב-I אם לכל  קיים
קיים 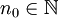 כך שאם
כך שאם 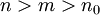 אז
אז 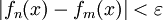 ב-I.
ב-I.
משפט 5
סדרת פונקציות 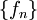 בקטע I מתכנסת במ"ש ב-I אם"ם היא מקיימת תנאי קושי במידה שווה.
בקטע I מתכנסת במ"ש ב-I אם"ם היא מקיימת תנאי קושי במידה שווה.
הוכחה
תחילה נניח שקיים 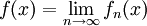 במ"ש ונראה שתנאי קושי מתקיים. לצורך זה יהי
במ"ש ונראה שתנאי קושי מתקיים. לצורך זה יהי  נתון. לפי הנתון ש-
נתון. לפי הנתון ש-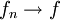 במ"ש ב-I, קיים
במ"ש ב-I, קיים 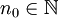 כך שאם
כך שאם 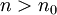 אז
אז 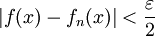 לכל
לכל 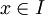 .
.
כעת אם 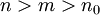 אז לכל
אז לכל 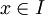 מתקיים
מתקיים 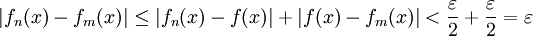 .
.
לצד השני, נניח ש-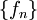 מקיימת תנאי קושי במ"ש ב-I. ניקח
מקיימת תנאי קושי במ"ש ב-I. ניקח 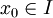 כלשהו ונעיר שסדרת המספרים
כלשהו ונעיר שסדרת המספרים 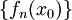 היא סדרת קושי (כי עפ"י הנתון לכל
היא סדרת קושי (כי עפ"י הנתון לכל  קיים
קיים 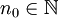 כך שאם
כך שאם 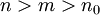 אז
אז 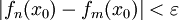 ) ולפי משפט קושי מאינפי 1 קיים גבול
) ולפי משפט קושי מאינפי 1 קיים גבול 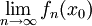 . הדבר נכון לכל
. הדבר נכון לכל 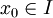 וכך נוצרת פונקציה גבולית
וכך נוצרת פונקציה גבולית 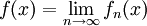 . נותר להוכיח שההתכנסות במ"ש. יהי
. נותר להוכיח שההתכנסות במ"ש. יהי  נתון. עפ"י תנאי קושי יש
נתון. עפ"י תנאי קושי יש 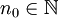 כך שלכל
כך שלכל 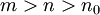 מתקיים
מתקיים 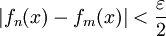 לכל
לכל 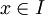 . כעת נבחר
. כעת נבחר 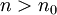 מסויים ולכל
מסויים ולכל 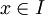 נשאיף
נשאיף 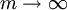 כלומר
כלומר 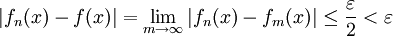 . לכן הוכחנו ש-
. לכן הוכחנו ש-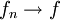 במ"ש ב-I.
במ"ש ב-I. 
טורי פונקציות
נאמר שהטור 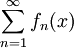 מתכנס ל-
מתכנס ל-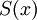 במ"ש על I אם
במ"ש על I אם 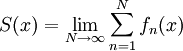 במ"ש על I.
במ"ש על I.
הגדרה: הטור 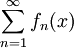 מקיים תנאי קושי במ"ש ב-I אם לכל
מקיים תנאי קושי במ"ש ב-I אם לכל  קיים
קיים 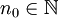 כך שאם
כך שאם 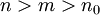 אז
אז 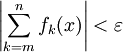 לכל
לכל 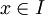 .
.
משפט 6
הטור 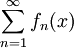 מתכנס במ"ש על I אם"ם הוא מקיים את תנאי קושי במ"ש ב-I.
מתכנס במ"ש על I אם"ם הוא מקיים את תנאי קושי במ"ש ב-I.
הוכחה
לפי הגדרה 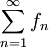 מתכנס במ"ש על I אם"ם סדרת הסכומים החלקיים
מתכנס במ"ש על I אם"ם סדרת הסכומים החלקיים 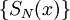 מתכנסת במ"ש על I. לפי משפט 5 זה קורה אם"ם
מתכנסת במ"ש על I. לפי משפט 5 זה קורה אם"ם 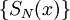 קושי במ"ש על I, כלומר אם"ם לכל
קושי במ"ש על I, כלומר אם"ם לכל  קיים
קיים 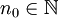 כך שאם
כך שאם 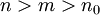 אזי
אזי 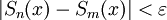 לכל
לכל 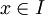 , שמתקיים אם"ם
, שמתקיים אם"ם 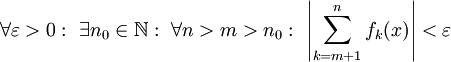 לכל
לכל 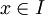 וזה שקול לתנאי קושי להתכנסות הטור במ"ש על I.
וזה שקול לתנאי קושי להתכנסות הטור במ"ש על I. 
משפט 7 (מבחן ה-M של ויירשטראס, Weierstrass M-test)
נניח שלכל n הפונקציה 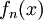 מוגדרת ב-I וחסומה שם:
מוגדרת ב-I וחסומה שם: 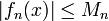 לכל
לכל 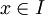 . עוד נניח שהסכום
. עוד נניח שהסכום 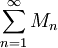 מתכנס במובן הצר. אזי
מתכנס במובן הצר. אזי 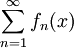 מתכנס במ"ש על I.
מתכנס במ"ש על I.
הוכחה
נסתמך על משפט 6 לומר שמספיק להוכיח שהטור 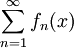 מקיים תנאי קושי ב-I. לצורך זה יהי
מקיים תנאי קושי ב-I. לצורך זה יהי  נתון. כיוון ש-
נתון. כיוון ש-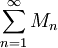 מתכנס הוא טור קושי של מספרים. לכן קיים
מתכנס הוא טור קושי של מספרים. לכן קיים 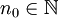 כך שאם
כך שאם 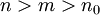 אזי
אזי 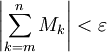 , כלומר
, כלומר 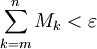 (כי
(כי 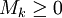 ). כעת אם
). כעת אם 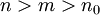 אז לכל
אז לכל 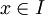 מתקיים
מתקיים 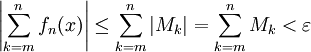 ובזה קיימנו את תנאי קושי להתכנסות הטור
ובזה קיימנו את תנאי קושי להתכנסות הטור 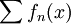 במ"ש על I.
במ"ש על I. 
מסקנה
בתנאים של מבחן ויירשראס, אם 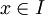 אזי
אזי 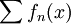 מתכנס בהחלט.
מתכנס בהחלט.
הוכחה
נקח 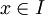 כלשהו. לפי הנתון
כלשהו. לפי הנתון 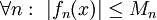 וכן
וכן 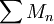 מתכנס בהחלט. ע"פ מבחן ההשוואה
מתכנס בהחלט. ע"פ מבחן ההשוואה 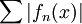 מתכנס.
מתכנס. 
דוגמה
נוכיח שהטור ההנדסי 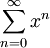 מתכנס נקודתית בקטע
מתכנס נקודתית בקטע 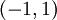 אבל לא במ"ש ונוכיח שאם
אבל לא במ"ש ונוכיח שאם 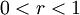 הטור מתכנס ב-
הטור מתכנס ב-![[-r,r]](/images/math/4/1/b/41b4ab49507fdfa895adf70e230ce557.png) : כבר הוכחנו שאם
: כבר הוכחנו שאם 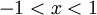 אז
אז 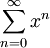 מתכנס ל-
מתכנס ל-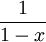 .
.
נראה כי ההתכנסות אינה במ"ש. כל סכום חלקי 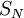 חסום בקטע
חסום בקטע 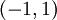 :
: 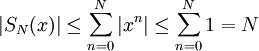 . אם היה נכון ש-
. אם היה נכון ש-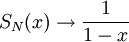 במ"ש ב-
במ"ש ב-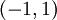 היינו מסיקים מהתרגיל בתחילת ההרצאה שהפונקציה
היינו מסיקים מהתרגיל בתחילת ההרצאה שהפונקציה 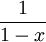 חסומה וזה אינו נכון. לכן ההתכנסות לא במ"ש.
חסומה וזה אינו נכון. לכן ההתכנסות לא במ"ש.
נותר להוכיח שאם 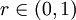 אז
אז 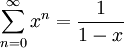 במ"ש על
במ"ש על ![[-r,r]](/images/math/4/1/b/41b4ab49507fdfa895adf70e230ce557.png) . ובכן בקטע
. ובכן בקטע ![[-r,r]](/images/math/4/1/b/41b4ab49507fdfa895adf70e230ce557.png) מתקייים
מתקייים 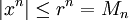 כאן
כאן 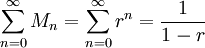 . כיוון שסכום החסמים מתכנס מבחן ויירשראס אומר ש-
. כיוון שסכום החסמים מתכנס מבחן ויירשראס אומר ש-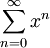 מתכנס במ"ש ב-
מתכנס במ"ש ב-![[-r,r]](/images/math/4/1/b/41b4ab49507fdfa895adf70e230ce557.png) .
. 
משפט 8
נניח ש-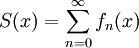 עם התכנסות במ"ש על I. אם עבור איזה
עם התכנסות במ"ש על I. אם עבור איזה 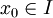 כל
כל 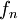 רציפה ב-
רציפה ב- אז גם S רציפה ב-
אז גם S רציפה ב- .
.
הוכחה
לכל N הסכום החלקי 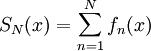 סכום סופי של פונקציות רציפות ב-
סכום סופי של פונקציות רציפות ב- .
.
מאינפי 1 ידוע ש-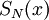 רציפה ב-
רציפה ב- עבור כל N. נתון
עבור כל N. נתון 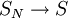 במ"ש על I.
במ"ש על I.
לכן נובע ממשפט 2 ש-f רציפה ב- .
. 
מסקנה
בתנאים של משפט 8, אם כל 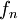 רציפה ב-I כולו אז גם S רציפה ב-I כולו.
רציפה ב-I כולו אז גם S רציפה ב-I כולו.
משפט 9
נניח 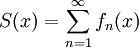 במ"ש על
במ"ש על ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . עוד נניח שכל
. עוד נניח שכל 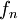 אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי S אינטגרבילית ב-
. אזי S אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-
ו-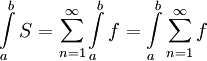 .
.
הוכחה
כרגיל נגדיר סכומים חלקיים 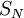 ונתון
ונתון 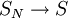 במ"ש על
במ"ש על ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
לפי משפט 3
.
לפי משפט 3 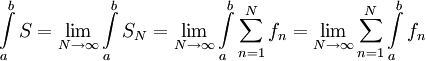 כי לסכום סופי ידוע שהאינטגרל של הסכום הוא סכום האינטגרלים. מצאנו שקיים גבול
כי לסכום סופי ידוע שהאינטגרל של הסכום הוא סכום האינטגרלים. מצאנו שקיים גבול 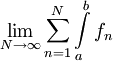 ולפי הגדרת סכום אינסופי הגבול הוא
ולפי הגדרת סכום אינסופי הגבול הוא 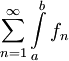 , והוא שווה ל-
, והוא שווה ל-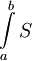 .
. 
משפט 10
יהי 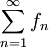 טור של פונקציות בעלות נגזרות רציפות ב-I. נניח:
טור של פונקציות בעלות נגזרות רציפות ב-I. נניח:
- עבור נקודה
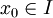 אחת לפחות הטור
אחת לפחות הטור 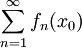 מתכנס.
מתכנס. - טור הנגזרות
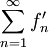 מתכנס במ"ש לפונקציה s על I.
מתכנס במ"ש לפונקציה s על I.
אזי 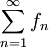 מתכנס במ"ש על I לפונקציה גזירה S ומתקיים
מתכנס במ"ש על I לפונקציה גזירה S ומתקיים 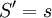 . בפרט, בתנאים אלה
. בפרט, בתנאים אלה 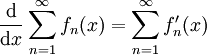 .
.
את ההמשך עשינו בהרצאה שאחריה:
הוכחה
נגדיר סכומים חלקיים 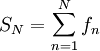 . הנתון הראשון אומר שלפחות בנקודה
. הנתון הראשון אומר שלפחות בנקודה 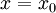 קיים
קיים 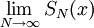 . הנתון השני אומר שקיים
. הנתון השני אומר שקיים 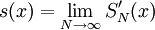 במ"ש ב-I. ז"א הסדרה
במ"ש ב-I. ז"א הסדרה 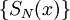 מקיימת את התנאים של משפט 4 ולכן קיים
מקיימת את התנאים של משפט 4 ולכן קיים 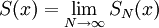 ב-I כך ש-S גזירה ב-I ו-
ב-I כך ש-S גזירה ב-I ו-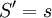 . עתה
. עתה 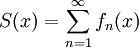 וכן
וכן 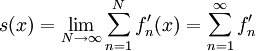 . מכיוון ש-
. מכיוון ש-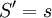 נסיק
נסיק 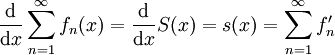 .
. 
דוגמה ממבחן
לכל 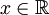 נגדיר
נגדיר 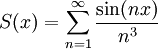 . הוכיחו ש-S מוגדרת היטב (ז"א הטור מתכנס לכל
. הוכיחו ש-S מוגדרת היטב (ז"א הטור מתכנס לכל 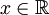 ) ו-S בעלת נגזרת רציפה לכל
) ו-S בעלת נגזרת רציפה לכל 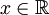 .
.
פתרון
לפי מבחן ה-M של ויירשראס, נמצא חסם עליון לערך המוחלט איברי הטור: 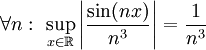 . כעת
. כעת 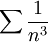 מתכנס, לכן
מתכנס, לכן 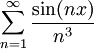 מתכנס במ"ש על
מתכנס במ"ש על 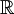 , כלומר S מוגדרת היטב. נותר להוכיח ש-
, כלומר S מוגדרת היטב. נותר להוכיח ש-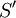 קיימת ורציפה. נעזר במשפט 10: הטור
קיימת ורציפה. נעזר במשפט 10: הטור 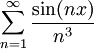 מתכנס בכל נקודה ב-
מתכנס בכל נקודה ב-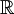 וכן הטור הגזור איבר-איבר הוא
וכן הטור הגזור איבר-איבר הוא 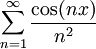 . לכל n מתקיים
. לכל n מתקיים 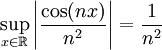 ו-
ו-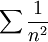 מתכנס. ע"י מבחן ה-M של ויירשראס נסיק שהטור הגזור מתכנס במ"ש על
מתכנס. ע"י מבחן ה-M של ויירשראס נסיק שהטור הגזור מתכנס במ"ש על 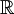 ולכן
ולכן 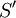 קיימת ובפרט
קיימת ובפרט 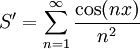 . ברור כי
. ברור כי 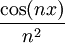 רציפה ב-
רציפה ב-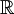 ולכן, מכיוון שההתכנסות ל-
ולכן, מכיוון שההתכנסות ל-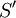 במ"ש, גם
במ"ש, גם 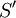 רציפה (לפי משפט 8).
רציפה (לפי משפט 8). 