לינארית 2 לתיכוניסטים תש"ע

$\begin{bmatrix} \lambda & 0 & 0 \\ 0 &\lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix}$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחתית הדף את השורה הבאה:

== כותרת שאלה ==

לכתוב מתחתיה את השאלה שלכם, וללחוץ על 'שמירה'.

(אין צורך להרשם לאתר. רק לעקוב אחרי ההוראות הפשוטות...)

ארכיון

ארכיון 1 - שאלות על תרגילים 1-4

ארכיון 2 - שאלות על תרגילים 5-8

ארכיון 3 - שאלות על תרגילים 10-11

ארכיון 4 - שאלות על תרגיל 12 והמבחן

שאלות

שאלה

איך מוכיחים שאם שתי מטריצות דומות אז לכל עע שלהן יש אותו ריבוי גיאומטרי. חשבנו אולי להשתמש בצורת ג'ורדן אבל לא נתון שהפולינום שלהן מתפרק לגורמים לינארים.

ועוד שאלה

בהוכחה של המשפט, שלV מ"ו מעל R יש ת"מ אינווריאנטי ממימד 1 או 2 סימנו את הע"ע המרוכב והו"ע המרוכב לפי ממשי + i מדומה ואז קיבלנו ש: שתי משוואות שמקשרות בין המטריצה, החלקים המדומים\ממשיים של הו"ע והע"ע. איך ממשיכים הלאה? איך זה עוזר?

תשובה

מעל המרוכבים קיים ל$A$ וקטור עצמי אחד לפחות עם ע"ע אחד לפחות תמיד. [תרגיל: האם יכול להיות שקיים רק אחד?]

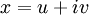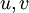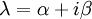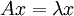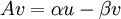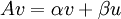נסמן $x=u+iv$ ו"ע כאשר $u,v$ וקטורים ממשיים, ונסמן $\lambda = \alpha + i\beta$ הע"ע המתאים. לכן $Ax=\lambda x$ נפתח את הביטוי, נשווה את הצד הדמיוני והממשי ונקבל 2 משוואות $Av=\alpha u - \beta v$ ו $Av=\alpha v + \beta u$. אז רואים בקלות שלכל וקטור 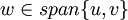$w \in span\{u,v\}$ מתקיים 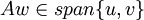$Aw \in span\{u,v\}$ ולכן האופרטור אינווריאנטי תחת התת מרחב $span\{u,v\}$.

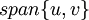תודה! (:

שאלה

למה לכל פונ' ריבועית כללית יש את הצורה q(x)=(x^t)Ax ?

תשובה

ראינו בתרגיל שכל תבנית ריבועית 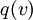$q(v)$ מתאימה לתבנית בי לינארית סימטרית 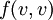$f(v,v)$, ולמדנו שלכל תבנית בי לנארית יש מטריצה $[f]$ כך ש$f(v,u)=v^t[f]u$ ולמדנו שהמטריצה של תבנית בי לינארית היא סמטרית אם"ם התבנית סמטרית.

שאלה

מישהו אמר לי ששאלו את מרצה הקבוצה השנייה האם יהיה פירוק פולרי במבחן והוא אמר שלא...יש מישהו שיכול לאמת את זה כדי שאהיה בטוח?

שאלה

האם ידועה החלוקה בין ציון הבוחן, המבחן ושיעורי הבית? האם יש אפשרות ליידע את כולנו בממוצע הציונים בשיעורי הבית, כולל שיעורי הבית האחרונים? תודה רבה!!

שאלה

כתבנו בהרצאה על שניוניות ש אפשר לסדר את הע"ע של T האופרטור הצל"ע בסדר כזה, כך שהראשונים יהיו שונים מ0, ובסוף יהיו שווים ל0, ושהRANK של T שקול למס' הע"ע השונים. למה זה?

טוב הבנתי לבד חח, זה בגלל שהראנק של אופרטור שקול לראנק של ההצגה שלו לפי בסיס כלשהו ללא תלות בבסיס...