אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
ארכיון
ארכיון 1 - תרגיל 1 ו2
ארכיון 2 - תרגיל 3
שאלה
מבקשים ממני נקודות קיצון - האם אני יכול להסיק על סמך עליות וירידות של הפונקצייה את נק' הקיצון שלה? כלומר, יש לי פונקצייה שבדיעבד אני מגלה שהנגזרת בנקודה לא קיימת, אבל אני רואה את ההתנהגות של הנגזרת בשני צידיה. למה, בעצם, הייתי צריך לחשב את הנגזרת בנקודה שלה (גם אם היא כן הייתה קיימת)?
שאלות
שאלות
א)ב1 להחשיב משולש עם שטח 0 כמשולש? ב)הקבוצה של תומר בסוף לא מגישה את תר' 4 נכון? תודה
תשובה
א. כבר שאלו את זה. צריך משולש ישר זוית שהצלעות שלו הם הצירים וקו ישר דרך נקודה מסוימת. נקודה בודדת פשוט לא עונה על התנאים האלה.
ב. לא יודע, ה תלוי בתומר תשובה - תומר : לגבי שאלה 4 - עם קבוצת יום ראשון "שלי" פתרנו מספר אינטגרלים בעזרת אינטגרציה בחלקים , ולכן ניתן לפתור את שאלה 4 . הקבוצה של המרצה רוני מיום שלישי לא ראתה תרגילים כנ"ל איתי ולכן לא צריכה לפתור את שאלת האינטגרלים .
תומר
שאלה
ב-1א אין מס' שהוא השטח המקסימלי.....זה אינסוף..... אם כן,מה עליי לכתוב?אין מס' שהוא שטח מקסימלי? תשובה - תומר : אם קיים שטח מקסימלי (מספרי ! ) יש לרשום מהו , אך אם אין מספר ממשי שהוא השטח המקסימלי (מסיבה שיש לנמק... ) - יש לרשום זאת .
תומר .
שאלה
מתי מגישים את תרגיל 3?
תשובה
מיד אחרי החופש
תרגיל 3 - 2
לגבי נקודות פיתול. ההגדרה בכלל לא מתייחסת לקיום של משיק בנקודת פיתול, אז אני לא מבין מדוע מתייחסים לכך.סה"כ צריכה להיות סביבה מימין/שמאל שבה הפונקציה קמורה/קעורה וסביבה מהצד השני בה מתקיים ההפך,כך שאין בדיוק התייחסות למשיק בנקודה הזאת. אם אפשר הבהרה לגבי זאת.
תשובה
סביבה מסביב לנקודה, בה הפונקציה קעורה או קמורה ביחס לנקודה, כלומר ביחס למשיק בנקודה. עדיין,למה צריך שיהיה משיק בנקודה הזאת (כלומר קיום נגזרת ראשונה בנקודה). ואם השיפוע של המשיק הוא אינסוף (משהו מהצורה a/0) או מינוס אינסוף אז זאת בהכרח לא נקודת פיתול?
שאלה- זוגיות ואי זוגיות
אם אני רוצה להראות שפונקציה מסוימת אינה זוגית ואינה אי זוגית, האם עלי להראות זאת ממש ע"י הצבת נקודות וסתירת הזוגיות והאי זוגיות, או שאני יכול פשוט להציב 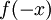 ולהראות שאני לא מקבל לא את
ולהראות שאני לא מקבל לא את  ולא את
ולא את 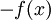 ?
?
=תשובה
לא מבין את ההבדל. פונקציה היא אינה זוגית אם קיימת נקודה אחת a בה 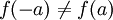 .
.
כמו כן, היא אינה אי זוגית אם קיימת נקודה b כך ש 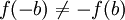 .
.
זו שלילה לוגית פשוטה להגדרה.
- לא הבנת את השאלה שלי. הכוונה שלי הייתה האם עלי להצביע על נקודה שאינה מקיימת את הזוגיות/אי זוגיות ולהראות שהיא אינה מקיימת את זה, או להציב בפונקציה -X ולהראות שאני לא מקבל את הדרוש. כי בעצם יכול להיות שאחרי שאני מציב מינוס X יש דרך שאני לא רואה לפתח את הביטוי שהתקבל ולקבל שהפונקציה זוגית/אי זוגית. אז האם עלי להצביע על נקודה שסותרת את הזוגיות/אי זוגיות, או שאני יכול באופן כללי להציב מינוס X ולהראות שאני מקבל ביטוי שאינו
 או
או 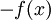 ?
?
- אתה חייב להבין שאין הבדל בין 2 השיטות. אני אסביר שיטתית:
- הצבת מינוס x וקיבלת ביטוי
- פיתחת את הביטוי הנ"ל והראת שהוא אינו
 או
או 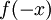
- לפי הגדרה, אם הביטוי שקיבלת הוא אינו
 כלומר קיימת נקודה בה הביטוי שהגעת אליו ו
כלומר קיימת נקודה בה הביטוי שהגעת אליו ו שונים. מכיוון שפונקציות שוות אם"ם הן שוות בכל נקודה.
שונים. מכיוון שפונקציות שוות אם"ם הן שוות בכל נקודה.
לסיכום, הניסוח לא משנה. קל יותר להראות סתירה על ידי מציאת נקודות a,b כפי שתארתי למעלה.
לדוגמא:
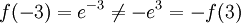 ולכן הפונקציה
ולכן הפונקציה 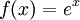 אינה אי זוגית
אינה אי זוגית
- הנקודה שלי הייתה שאחרי שהצבת
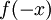 אין דרך לדעת שזה לא שווה ל
אין דרך לדעת שזה לא שווה ל  עד שלא הצבת איזשהו X וראית שמתקבלים ערכים שונים. השאלה שלי היא אם צריך להראות את ההצבה הזאת, או שמספיק לאמר שהגענו לשני ביטויים שונים, שבטוח קיים איזשהו X שאם מציבים אותו בשני הביטויים מקבלים ערכים שונים.
עד שלא הצבת איזשהו X וראית שמתקבלים ערכים שונים. השאלה שלי היא אם צריך להראות את ההצבה הזאת, או שמספיק לאמר שהגענו לשני ביטויים שונים, שבטוח קיים איזשהו X שאם מציבים אותו בשני הביטויים מקבלים ערכים שונים.
- הנקודה שלי הייתה שאחרי שהצבת
- שום דבר לא בטוח עד שלא בודקים אותו. אם הגעת נגיד לביטויים סינוס וקוסינוס ניתן לאמר שהם שונים כי זה ידוע שיש נקודות שתציב שיתנו תוצאות שונות. אם הגעת לביטויים לא מוכרים אתה חייב להציב.
שאלה
אם פונקציה מוגדרת לכל X, אז בוודאות אין לה אסימפטוטה אנכית?
(זה לא ארז) לא בהכרח. למשל הפונקציה f(x)=1/x כאשר x>0 ו f(x)=0 כאשר x<=0, מוגדרת לכל x ממשי אבל יש לה אסימפטוטה אנכית X=0, כי הגבול ב-0 מימין הוא אינסוף. לעומת זאת- אם פונקציה רציפה אז בוודאות אין לה אסימפטוטה אנכית, כי אם למשל x=a אסימפטוטה אנכית אז לפי רציפות הגבול ב x=a שווה לערך הפונקציה בנקודה זו, שלא יכול להיות אינסופי(כי הפונקציה רציפה ובפרט מוגדרת).
שאלה
בשאלה 3, מה הכוונה לחשב בכל נק'? לחקור?
תשובה
להגיד מה הערך בכל נקודה, בלי מחשבון (כלומר בלי להפעיל את הפונקציה arctan). תנסה להבין קצת את הפונקציה ותראה שזה לא מסובך
שאלה
היי ארז, בתרגול הזכרת איזה משפט שאומר שאם פונקציה גזירה פעמיים בקטע כלשהו, והיא מחליפה סימן כשהיא עוברת בנקודה מסוימת, אז זה אומר שזאת נקודת פיתול. אנחנו (בקבוצה של ד"ר שיין) לא הזכרנו את המשפט הזה בהרצאה.אשמח אם תכתוב פה את נוסח מדויק פחות או יותר של המשפט, עם כיוון פחות או יותר להוכחה שלו.
תשובה
נסתכל על פיתוח טיילור 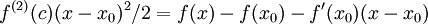 . משמאל זו השארית, ומימין זה ההפרש בין הפונקציה לבין המשיק בנקודה
. משמאל זו השארית, ומימין זה ההפרש בין הפונקציה לבין המשיק בנקודה  . ברור שהסימן של הצד השמאלי נקבע אך ורק על פי סימן הנגזרת השנייה, כאשר
. ברור שהסימן של הצד השמאלי נקבע אך ורק על פי סימן הנגזרת השנייה, כאשר 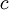 נמצא בין
נמצא בין  ו
ו  .
.
לכן אם הנגזרת השנייה מקבלת סימן אחד בסביבה ימנית של  וסימן הפוך בסביבה שמאלית, אז בצד עם הסימן השלילי הפונקציה מתחת למשיק, ובצד עם הסימן הימני הפונקציה מעל המשיק. ולכן זו נקודת פיתול.
וסימן הפוך בסביבה שמאלית, אז בצד עם הסימן השלילי הפונקציה מתחת למשיק, ובצד עם הסימן הימני הפונקציה מעל המשיק. ולכן זו נקודת פיתול.
זו אגב גם ההוכחה למה שרשמתי כשקורה שמתאפסות כל הנגזרות עד שלב n.
- היי ארז, אנא קרא זאת בעיון: מה שאתה רשמת, מוכיח שאם הנגזרת השנייה בנקודה כלשהי היא חיובית אז הפונקציה קעורה בה כלפי מעלה, ולהפך. נקודת פיתול לפי ההגדרה היא נקודה אשר אם מעבירים בה משיק אז מצד אחד המשי הוא מעל הפונקציה ומהצד השני הוא מתחת לפונקציה. ההגדרה של נקודת פיתול כלל לא מדברת על שינוי קעירות. אם אנחנו יוצאים מנקודת הנחה שנקודת פיתול היא נקודה בה הפונקציה משנה קעירות אז מה שרשמת אכן מוכיח זאת, אבל אני לא רואה איך מההוכחה שלך נובע שזאת נקודת פיתול לפי ההגדרה שלה. ההוכחה צריכה להתמד במשיק אך ורק בנקודה x0 עצמה. אגב, פיתוח הטיילור שלך לא נכון.
(זה לא ארז) בפיתוח הטיילור צריך להיות באגף ימין מינוס f(x0) , אבל זה לא משנה את ההוכחה... וארז דווקא כן הוכיח לפי הגדרה- הוא הראה שההפרש בין הפונקציה לבין המשיק בנקודה x0 הוא חיובי,כלומר שהפונקציה מעל המשיק בנקודה x0, לכל x>x0 ולהפך בצד השני...כלומר הוכחה של נקודת פיתול לפי ההגדרה. בהוכחה מתייחסים למשיק בנקודה קבועה x0 ולא בנקודה משתנה x...
- תודה על התיקון יש שם עוד כמה טעויות, תקנתי את הנוסחא. מה שאמרת נכון. פשוט צריך לשים לב שהמשיק בנקודה x_0 הינו
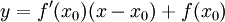 .
.
- אני חושב שהבנתי, תודה. :)
- ואיך מוכיחים שבנקודת פיתול פונקציה משנה את הקעירות שלה?
- כי אם יש נגזרת שניה רציפה בסביבה של נקודה, ואם היא חיובית בנקודה, אז הפונקציה קמורה כלפי מעלה בנקודה. זו בדיוק אותה הוכחה כמו למעלה, כי אם הנגזרת השנייה חיובית בנקודה היא חיובית בסביבה שלה (רציפות) ולכן בכל נקודה פרט לנקודת הפיתול הנגזרת השנייה היא בעלת סימן חיובי או שלילי בצד החיובי הפונקציה קמורה כלפי מעלה, ובצד השלילי כלפי מטה.
שאלה 2 - חקירת פונקציות של ערך מוחלט
כיצד ניתן לחשב נגזרת שנייה של ערך מוחלט? הצלחתי לחשב נגזרת ראשונה ע"י זה שנעזרתי ב-sign כנגזרת של ערך מוחלט כשהיא מוגדרת בפונקצייה, אבל איך אפשר להמשיך? גם כשניסיתי לחשב לפי הגדרת הגבול של הנגזרת (השנייה) קבלתי ביטוי באורך של שורה שכולל sign של לא מעט ביטויים (ארבעה, ליתר דיוק)... איך אפשר לפשט את זה?