אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 3.1 שאלה - תרגיל 5
- 3.2 שאלה - קבוצת ההרצאה של רוני ביתן
- 3.3 שאלה - תרגיל 5
- 3.4 שאלה - תרגיל 4
- 3.5 שאלה
- 3.6 שאלה - צמצום בחישוב אינטגרלים
- 3.7 שאלה
- 3.8 שאלה
- 3.9 שאלה
- 3.10 שאלה
- 3.11 שאלה תרגיל 5
- 3.12 שאלה על תרגיל מספר 4
- 3.13 שאלה תרגיל 4
- 3.14 שאלה
- 3.15 שאלה
- 3.16 שאלה
- 3.17 שאלה בקשר למשפט בתחילת תרגיל 6
- 3.18 שאלה
- 3.19 שאלה
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
ארכיון
ארכיון 1 - תרגיל 1 ו2
ארכיון 2 - תרגיל 3
ארכיון 3 - תרגיל 3
ארכיון 4 - תרגיל 4
שאלות
שאלה - תרגיל 5
לקבוצת התרגול של יום שלישי עדיין אין מושג איך לפתור את התרגילים האלה, ונראה שנצטרך לעשות אותם בשבוע הקרוב. האם מישהו מקבוצת יום ראשון, או אולי אפילו ארז, יכול להעלות לאתר את התרגילים שפתרתם אתמול בכיתה?
תשובה
כמו שאמרתי, אנחנו נעלה דפי עזר בקרוב (ברגע שאקרובט יחזור לעבוד לי ואני יוכל לייצא את המסמך).
- אין שום סיבה להשתמש באקרובט. למה שלא תנסה את PDFCreator?
אם מישהו יעלה גם את סיכום השיעור שלו זה גם יכול להיות נחמד.
תודה רבה!!
שאלה - קבוצת ההרצאה של רוני ביתן
מועד ההגשה שנקבע לתרגיל 6 מאוד בעייתי - בהנחה שמישהו הצליח לסיים את תרגיל 5 כולו היום (בדקתי בכיתה, בערך משהו כמו 3 מתוך 20 הצליחו לפתור ממנו משהו עד אתמול בתרגול), ומחר (חמישי) יש תרגול נוסף כדי לעבור על חומר לתרגיל 6 - הזמן היחידי שיהיה בימים הקרובים לפתור אותו (לדוגמא עבור אלה מאתנו ששומרים שבת) - שישי לפני כניסת שבת, מוצאי שבת, ויום שני.
כל זאת בהנחה שתרגיל 5 כבר פתור ומושלם, ובהתעלמות מוחלטת מהתרגיל הרצחני וההזוי בשימושי מחשב שקבלנו אתמול (שלישי) בלילה שגם הוא לשלישי הקרוב. אני לא רוצה להתלונן יתר על המידה, אבל באמת שזה בלתי אפשרי, ובוודאי שלא כשכולנו כתיכוניסטים צריכים גם ללמוד למבחני מתכונת בביה"ס ומ-8 בבוקר ועד 3-4 נמצאים בבי"ס.
מה אפשר לעשות בנוגע לדבר? תודה, ושבוע טוב!
- הבנתי שתומר דיבר איתכם בשיעור, אז אני לא בטוח מה השאלה.
שאלה - תרגיל 5
האם הקבוצה של ארז למדה את נוסחאות הרדוקצייה לחישוב אינטגרלים של חזקות של סינוסים וקוסינוסים (הגדרה רקורסיבית למציאת אינטגרל של סינוס/קוסינוס בחזקה שלמה כלשהי)? האם מותר להשתמש בה?
תשובה
לא יודע על איזה נוסחאות מדובר, אבל יש התייחסות למקרה הזה בדף על הצבות שהעלאתי לאתר. בעזרת הרשום שם ניתן לפתור את התרגיל.
- החזקות זוגיות, לכן השתמשתי בזהות טריג' והגעתי לאינטגרל שתלוי בסינוס בלבד, אבל בחזקות גבוהות. איך אני יכול לפתור את זה?
- וד"א, בדף ההצבות - למה הכוונה ב: R(sinx,cosx), למשל? לא הבנתי כ"כ את הרעיון.
- הנוסחא שהתכוונתי אליה היא נוסחא למציאת האינטגרל של כל סינוס בחזקה ה-n-ית, בעזרת רקורסייה (עד n=1).
- זו פונקציה רציונאלית שהצבת בה sinx וcosx. למשל
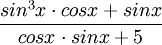
- זו פונקציה רציונאלית שהצבת בה sinx וcosx. למשל
- אפשר להשתמש בנוסחא כזו...
- אוקיי, ונניח שלא הייתי נתקל בנוסחא הזו. איך אחרת הייתי יכול לפתור את הבעייה הזו?
- אז אולי אני לא מבין על איזה נוסחא מדובר. אתה יכול לפתור את הבעייה עם הנוסחאות שבדף ההצבות בלבד.
- ארז - אני מקבוצת התרגול של יום שלישי. אמרת שכדאי לפתור את תרגיל 5 כבר מעכשיו, כי בעוד שבועיים נצטרך להגיש שני תרגילים. יש סיכוי שאתה מעלה חלק מהדפים של התרגול, או מישהו אחר? או לדחות את הגשת תרגיל 6, כשיגיע, לקבוצה של תומר לשבוע שאח"כ? ישבתי היום משהו כמו שעתיים על תרגיל 5, וכמה שניסיתי - הצלחתי לפתור רק את שאלה 1. בשבוע הבא לא יהיה לי זמן בכלל כתוצאה משתי מתכונות ומבחן בבי"ס, והבוחן בשימושי מחשב.
- אז אולי אני לא מבין על איזה נוסחא מדובר. אתה יכול לפתור את הבעייה עם הנוסחאות שבדף ההצבות בלבד.
- אוקיי, ונניח שלא הייתי נתקל בנוסחא הזו. איך אחרת הייתי יכול לפתור את הבעייה הזו?
- דף הסבר ההצבות נותן את כל ההצבות הדרושות על מנת לפתור את התרגיל. שאלות כמו 2, 3 ו4 לא ראינו בכיתה כלל והשאר בעזרת ההצבות שרשומות בדף ההסבר (ואף ברמזים!). אנחנו (המתרגלים) לא נעלה את דפי הסיכום שלנו, אתם מוזמנים לצלם את החומר מתלמידים אחרים. כדאי גם לקרוא בארכיון את מה שכתבתי על הצבה מהסוג
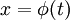
- דף הסבר ההצבות נותן את כל ההצבות הדרושות על מנת לפתור את התרגיל. שאלות כמו 2, 3 ו4 לא ראינו בכיתה כלל והשאר בעזרת ההצבות שרשומות בדף ההסבר (ואף ברמזים!). אנחנו (המתרגלים) לא נעלה את דפי הסיכום שלנו, אתם מוזמנים לצלם את החומר מתלמידים אחרים. כדאי גם לקרוא בארכיון את מה שכתבתי על הצבה מהסוג
שאלה 4 - רמזת בשאלה על הצבה טריגונומטרית היפרבולית. בדף הנוסחאות של הנגזרות יש נוסחא (הנוסחא התחתונה בצד ימין), טריגונומטרית היפרבולית, שהיא כמעט ישירות האינטגרל בשאלה. האם לזה התכוונת?
- אתה מוזמן להשתמש באיזה הצבה שתפתור את התרגיל. שימו לב שהנוסחאות להיפרבוליות הן טיפה שונות. למשל
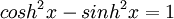 וכדומה...
וכדומה...
שאלה - תרגיל 4
בשאלה מס' 4, סעיף ד' - כשאתם אומרים ש"מספיק להגיע לאינטגרל פונקצייה רציונלית, ללא פתרון שלא" - האם הכוונה היא שמותר שהפונקצייה באינטגרל הזה תהיה תלוייה ב-t (כלומר מבלי להציב אח"כ את המשתנה המקורי)?
תשובה
צריך להגיע לאינטגרל של פונקציה רציונלית של t
- מצוין, תודה!
שאלה
היי ארז, זה בנוגע לשאלה 2 בתרגיל 4. רציתי לדעת אם הבנתי נכון.. (ככה תומר עשה בתרגול, בערך, אבל אני לא בטוחה שהבנתי את זה ב100%): בשאלות מסוג שאלה 2 בש.ב שלנו (כלומר, לחשב אינטגרל של פונקציה שמחולקת למקרים.. x>=o וx>=1 או x שייך ל(0,1)), האם סדר העבודה הוא הבא: ראשית מוצאים את הקדומה בקטעים הפתוחים. (כאן, למשל, הנק' הבעייתיות הן 0 ו1) לאחר מכן, משתמשים במשפט: אם קיימת F רציפה בסביבת x0 וגזירה בסביבה זו (פרט אולי לx0) וקיימת limF'x=l כשx->x0, אז F גזירה בxo וגם F'x0=l? כלומר, מחשבים את הגבולות מימין ומשמאל של הנגזרת בנק' הבעייתיות, מראים שהגבולות שווים ולכן יש גבול בנק' עצמה, ומכך נובע שF'x0=l (כלומר F גזירה בx0) - וכך מוצאים לאן לשייך בעצם את הנק' הבעייתיות, ע"י הגזירה? השלב הבא לאחר מכן, הוא לטעון שהפונקציה הקדומה F גזירה בנק' הבעייתיות (לפי מה שהראינו מקודם) ולכן גם רציפה בנק' אלה, ולכן הגבולות החד צדדיים קיימים ושווים, וכך למצוא את הקבועים (להביע את כל הקבועים באמצעות קבוע אחד)..?
תשובה
שימי לב שבציטוט המשפט הראשון אמרת שf רציפה, ואז את מסיקה שהיא גזירה ואז את מסיקה מהגזירות שוב את הרציפות, זה אסור. את צריכה לבנות את הפונקציה כך שהיא תהיה רציפה, ואחרי זה למצוא את הגבולות של הנגזרת שלה בנקודות הבעייתיות.
התהליך הוא הפוך, בקטעים הפתוחים את יכולה לבחור את הקבוע C שנוסף לקדומה. הקבוע הזה מאשפר לך ליצור פונקציה קדומה רציפה, ואז את יכולה להוכיח את מה שאת רוצה לגבי נגזרתה... שימי לב ששינוי הקבוע בקטעים הפתוחים לא ישנה את הערך באף נקודה של הנגזרת (פרט לנקודות הבעייתיות כמובן, שם הנגזרת תהיה מוגדרת תחת בחירת הקבועים המתאימים).
תחשבי על הדוגמא של קו ישר, שחתכת אותו באמצע והרמת חצי ממנו למעלה. השיפוע של הקו הישר הוא אותו דבר בכל מקום, אבל בנקודת החיתוך פתאום אין לו נגזרת כי הוא לא רציף שם כלל. אם תתקני את הקו ותחזירי אותו למקומו הוא יחזור להיות גזיר.
המצב פה דומה. הפונקציה הקדומה מורכבת מכמה "חתיכות" שנובעות מהקטעים הפתוחים. יש להדביק חתיכות אלה יחד על מנת ליצור פונקציה גזירה בנקודות החיבור. ההדבקה מתבצעת ע"י הזזה למעלה או למטה (תוספת קבוע C)
שאלה - צמצום בחישוב אינטגרלים
נניח שיש לי פונקצייה, ואני מעוניין לחשב את הקדומה שלה. האם מותר לי לצמצם את הפונקצייה המקורית איך שאני רוצה? (למשל, בתרגיל 4 בשאלה 4 ג' מתבקש לצמצם בשורש של e ב-x)
תשובה
מה הכוונה בלצמצם? אם אתה לא משנה את הפונקציה או את תחום הגדרתה זה בסדר. אם אתה כן משנה את הפונקציה או את תחום הגדרתה זה לא בסדר.
שאלה
1.באינטגרל מספר 5, להניח ש-a אינו 0?
2. מותר לבצע הצבות שונות מאלו שכתובות בתרגיל?
תשובה
תטפלו גם במקרה a=0
אפשר לעשות איזה הצבה שרוצים.
שאלה
היי ארז. אתה יכול בבקשה להעלות דף עם הנוסחה הרקורסיבית לאינטגרלים של sin ו-cos בחזקות גבוהות? וגם את העניין של הצבה טריג' היפרבולית..אנחנו לא יודעים מה זה בכלל. תודה!
תשובה
אתם צריכים להיות מסוגלים לפתור את זה לבד (בעזרת נוסחאות זוית כפולה כפי שרשום בדף ההסבר לגבי הצבות). ולגבי הצבות היפרבוליות, העלאתי דף עם כל הנגזרות וההגדרה של הפונקציות ההיפרבוליות (sinh,cosh,tanh...) אין שום דבר נוסף שאני יכול לחדש בעניין.
שאלה
מותר להשאיר אינטגרל של cos(x)^3 או שצריך להמשיך לפשט?
תשובה
יש להמשיך לפתור, כמו שרשום בכותרת התרגיל (יש לפשט דברים לצורתם הבסיסית ביותר)
תומר - חברים , נסו למצוא נוסחת רקורסיה לחישוב אינטגרלים של חזקות זוגיות של SIN ... ואז לנסות להגיע בתרגיל עם מכפלת חזקות זוגיות של COS ן SIN שיש לכם , לצורה של חזקה זוגית של SIN . בהצלחה !
שאלה
מה קורה אם בחישוב אינטגרל של פונקציה המוגדרת רק בתחום מסוים, מקבלים פונקציה קדומה שמוגדרת רק עבור תחום אחר.. הפונקציה לא אינטגרבילית?
תשובה
תלוי איך מקבלים את הקדומה. אולי ביצעת הצבה שעובדת רק בתחום מסוים?
שאלה תרגיל 5
מתי הקבוצה של תומר צריכה להגיש את תרגיל מספר 5?
שאלה על תרגיל מספר 4
בתרגול של תומר עשינו תזכורת כי אם f גזירה בקטע [a,b] ואם c ערך בין (f'+(a לבין (f'_(b אז קיים[ x0E[a,bכך ש:c =(f'(x0 ..... (שעות לקח לי לרשום את זה) קיצר אז הוא6 עשה דוגמא לשימוש במשפט כמו בתרגיל מספר 1 ג הוא נתן פונקציה שבx גדול שווה ל0 זה e בחזקת אחד חלקי X וב-0 ערכה 0... אך כאשר השתמש במשפט אמר שהערך שבינו לבין הערך נגיד 1 צריך להיות x0 הוא 0 למרות ש(f'+(0=אינסוף... מה פשר הטעות?
תומר - משהו התומר הזה ...:) לעניינינו - שים לב לאיזו פונקציה נתונה לך ? אני מציג לך פונקציה , ושואל , האם פונקציה זו יכולה להיות נגזרת של איזושהיא פונקציה אחרת . אנחנו ראינו/הזכרנו , שאם פונקציה f היא נגזרת של פונקציה אחרת , אז לפונקציה f (שהיא הנגזרת ! ) , יש את תכונת "ערך הביניים " הזו . בנוגע לשאלה בתרגיל - האם הפונקציה הנתונה יכולה להיות נגזרת של איזושהיא פונקציה אחרת ? ...
תומר .
שאלה תרגיל 4
יש לי שאלה אם אני מגיע לפולינום עם 1+sqrtx נקרא לזה t לשם הנוחיות שלי.. אני צריך לפתוח את( t בשלישית חלקי שלוש) פלוס t בריבוע פלוס t? כאילו עם הנסחאות כפל מקוצר של הבשלישית ושל הבריבוע או שלא צריך לפתוח ולשהשאיר את התשובה כך פשוט זה סתם ארוך...
שאלה
בשאלה 2 בתרגיל 4, אם בדקתי את הנגזרות החד צדדיות בכל אחת מהנק' הבעייתיות והראתי שמתקיימת הנגזרת בנקודות האלו (וממילא יצא שהפונ' רציפה), האם אני עדיין צריך להראות בנפרד בדיקה שזה (הרציפות של הפונ') מתקיים?
תשובה
העובדה שהנגזרות החד צדדיות שוות לא גוררת שהפונקציה גזירה בנקודה, לדוגמא 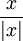 . ולכן זו שגיאה חמורה להגיד שכתוצאה מכך הפונקציה רציפה.
. ולכן זו שגיאה חמורה להגיד שכתוצאה מכך הפונקציה רציפה.
להפך, אם הפונקציה רציפה והנגזרות החד צדדיות שוות אז ניתן לומר שהפונקציה גזירה בנקודה.
שאלה
שלום, שוחחתי עם רוני,והוא אמר לי לשאול את המתרגלים עד איזו הרצאה הבוחן יהיה. לכן,החלטתי להעלות זאת כאן.אנו מבקשים שתקלו מעט בבקשה,כי אנו נמצאים בתקופת בגרויות,ובנוסף הבוחן כמעט בסוף הסמסטר כך שנלמד עד אז כבר הרבה נושאים,שמן הסתם הכנסתם של כולם תכביד על כולנו ללא הועיל. בנוסף רציתי לדעת האם יהיו הוכחות מהכיתה בבוחן?רוני אמר שבמבחן לא יהיו,ולכן תהיתי האם לבוחן יש טעם ללמוד אותם? תודה למתרגלים!
תשובה
שאלה טובה.
אנחנו נחליט את ההחלטות בהקשר לבוחן כבר השבוע, ונודיע ביום ראשון על התאריך ועל החומר לבוחן.
הוכחות מההרצאה בוודאי לא יהיו בבוחן, אם יהיה הוכחות בכלל ואיזה סוג של הוכחות נודיע ביום ראשון.
אני רק אומר, שמשתמע מדבריך שכדאי לא ללמוד את ההוכחות מהכיתה כלל כי הם לא יהיו במבחן. זו שגיאה חמורה, תמיד צריך ללמוד את ההוכחות, רק ככה באמת מבינים את החומר. בנוסף, תרגילים בבוחן ו/או מבחן, גם אם לא חוזרים בדיוק על הוכחות שראיתם בכיתה, לעיתים קרובות חוזרים על רעיונות של הוכחות מהכיתה.
שאלה
זה רק אני או שבתרגיל 6 שאלה 4 הפונקציה לא מוגדרת על כל הקטע [0,1]... אז איך היא יכולה בכלל להיות אנטגרבילית?
גם אני חושב שיש בעיה... אבל זה משהו די שולי- בהגדרת הפונקציה, במקום גדול שווה צריך להיות גדול ממש, כי אחרת הפונקציה אינה חד ערכית עבור נקודות מהצורה n/n+1
תשובה
הכותב השני צודק, האי שיוויון הימני צריך להיות חלש. אני אפרסם תיקון לתרגיל.
שאלה בקשר למשפט בתחילת תרגיל 6
היי ארז, הנוסח של המשפט שכתבת בתחילת התרגיל דומה למשפט שהוכחנו בהרצאה, אך ממש לא אומר אותו דבר.
בהרצאה הוכחנו שפונקציה f(x) היא אינטגרבילית בקטע [a,b] אם ורק אם היא חסומה שם, ולכל e>0 קיים d>0 כך שלכל חלוקה T של [a,b] שהפרמטר שלה קטן מ- d מתקיים ש 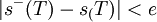 . המשפט שאתה כתבת כלל אינו מדבר על חסם של הפרמטר, אלא הוא דורש שפשוט תהיה קיימת חלוקה.
האם אתה בטוח שהמשפט נכון?
אם כן, זה אומר שפשוט מותר לי באופן אנליטי להסביר איך אני בונה את החלוקה שלי שלב אחרי שלב?
. המשפט שאתה כתבת כלל אינו מדבר על חסם של הפרמטר, אלא הוא דורש שפשוט תהיה קיימת חלוקה.
האם אתה בטוח שהמשפט נכון?
אם כן, זה אומר שפשוט מותר לי באופן אנליטי להסביר איך אני בונה את החלוקה שלי שלב אחרי שלב?
תשובה
אני מסכים שמשפט זה מבלבל, אבל ההוכחה דיי פשוטה.
נסמן ב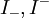 את האינטרגל העליון והתחתון. ברור שלכל חלוקה T מתקיים
את האינטרגל העליון והתחתון. ברור שלכל חלוקה T מתקיים
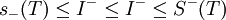
לכן, אם לכל אפסילון קיימת חלוקה כלשהי כך ש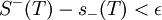 אזי מתקיים גם ש
אזי מתקיים גם ש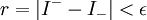 . אבל אם
. אבל אם 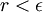 לכל אפסילון אזיי בהכרח
לכל אפסילון אזיי בהכרח 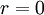
- הבנתי, תודה. :) אז בעצם אני יכול להסביר באופן אנליטי כיצד אני בונה את החלוקה שלי, שלב אחרי שלב?
- לא יודע מה זה להסביר באופן אנליטי :) אם תראה שלכל אפסילון קיימת חלוקה כך שההפרש בין סכום דרבו עליון לתחתון קטן מאפסילון אזי הפונקציה אינטגרבילית.
שאלה
בשאלה 1a בתרגיל 6- אני לא יודע איזה נקודות אי רציפות יש- יכול להיות משלושת הסוגים?
תשובה
יכול להיות מה שאתה רוצה. הנתון הוא שהפונקציה רציפה פרט למספר סופי של נקודות.
שאלה
בשאלה 1b- אפשר להבין את השאלה בשתי דרכים. האם הכוונה שהפונקציה הקדומה חייבת להיות גם היא מוגדרת בקטע [a,b] שבה מוגדרת f, או שאני יכול לתת f שמוגדרת בקטע מסוים אבל הקדומה שלה לא מוגדרת בכל נקודות הקטע הזה?
תשובה
אין שתי דרכים להבין את זה. F הינה קדומה של f בקטע [a,b] כלומר, f הינה הנגזרת של F בקטע הנ"ל. נובע שF בוודאי מוגדרת ואף רציפה וגזירה בקטע. f הינה הנגזרת שלה (בקטע זה). האם f אינטגרבילית.