אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות

$\lim_{n\rightarrow\infty}f_n$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - תרגיל 1 ו2

ארכיון 2 - תרגיל 3

ארכיון 3 - תרגיל 3

ארכיון 4 - תרגיל 4

ארכיון 5 - תרגיל 4,5

ארכיון 6 - תרגיל 6

ארכיון 7 - (מי עוקב)

ארכיון 8

ארכיון 9 - לקראת הבוחן

שאלות

תומר - לפני הבוחן , אתן לכם מעט מידע שניתן לחשוף : החומר לבוחן הוא כאמור כל החומר מתחילת הסמסטר , עד ולא כולל , אינטגרלים לא אמיתיים . אין צורך בנוסחאות - הכל תקבלו בכתב , ולא מותר שום חומר עזר ! יש בחירה שנראית לנו הוגנת ומי שלמד כמו שצריך עד עכשיו רק ייצא נשכר .מי שנזכר רק עכשיו - לא צריך להילחץ , יש עוד זמן וזו תהיה נקודת זמן לקחת תצמו בידיים ! - ורק תזכרו - מדובר רק בבוחן ! יש עוד דרך ארוכה עד סוף הסמסטר והמבחן הסופי . שיהיה בהצלחה לכולם !

שאלה - פונקציות טריגונומטריות ממעלה גבוהה

נניח שאני רוצה לחשב את האינטגרל של סינוס בחמישית של x. האם "חוקי", בהנחה שהצבתי 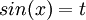$sin(x)=t$, להסיק ש: 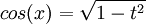$cos(x)=\sqrt{1-t^2}$ להמשך ההצבה? אם לא, באילו דרכים נוספות (מלבד ההצבה האוניברסאלית שלא נראית יעילה במיוחד והנוסחא לחישוב סינוס ממעלה גבוהה) ניתן לחשב את האינטגרל?

הערה : שמתי לב שמאחר וחזקת הסינוס היא אי-זוגית, נוח יותר להציב t=cosx. אני ממשיך לשאול את אותה שאלה באופן כללי.

תשובה

מוצאים את פיתרון האינטגרל על ידי הנוסחא הרקורסיבית: [[1]]

אם אתה צריך לחשב את האינטגרל של cos(x( ממעלה מסויימת אתה יכול להמיר אותו לאינטגרלים של sin(x) או שאתה יכול להשתמש בנוסחא: [[2]]

שאלה בקשר לבוחן

מה יהיו הנושאים בבוחן? איזה סוג של שאלות הוא יכלול? עברתי על כל התרגילים שנתנו עד כה (1-8), החל ממשפטי לגראנז' והערך הממוצע, דרך כלל לופיטל, חקירת פונקציות, טורי טיילור, עד לאינטגרלים הלא מסויימים, הצבות שונות, ולבסוף את כל הנושא של האינטגרביליות ועד לחישובים השונים של אינטגרלים מסויימים. אני די מתוסכל כי זה המון חומר ואשמח אם תוכלו לספק מידע, אפילו מועט, בנוגע לסוג השאלות שיופיעו בבוחן : האם תהיה בחירה? האם יהיו שאלות מסוג אמריקאי / נכון לא נכון? הוכח או הפרך? האם נצטרך לחקור פונקציות? תודה!

תשובה

ציינת יפה את רשימת החומר לבוחן.

יהיו שאלות הוכחה כלומר שאלות תאורטיות, ויהיו שאלות קצרות יותר בסגנון של הוכח הפרך (עם תשובה קצרה). צריך לדעת חקירת פונקציות, אבל לא נתן לכם לחקור פונקציה מלאה.

ותהרגו אותי אם אני מבין איך עוזר לכם לדעת אם תהיה בחירה או לא. אם המטרה היא לדלג על חומר מסוים מתוך ההנחה שתוכל לבחור לא לענות על שאלות בנושא, אני ממליץ לא לעשות את זה (כנראה שלא תהיה בחירה, וגם אם כן לא נאפשר לבחור בין נושאים שונים)

הסיבה היא בעיקר להרגיע אותנו - יהיה לך קשה למצוא סטודנטים רציניים שלא לחוצים מהבוחן הקרוב. אח"כ, המטרה שלשמה שאלתי את השאלה היא כדי לנסות ולמקד את תהליך הלמידה - בבחנים משנים קודמות קשה מאוד למצוא שאלות 'תאורטיות' או שאלות מסוג 'הוכח או הפרך', כך שמלבד חישוב אינטגרלים, חקירת פונקציות וחזרה עמוקה על החומר והתרגילים אין יותר מדי דרכים להתכונן לבוחן...

אם תדע לפתור תרגילים כמו בתרגילי הבית מצבך יהיה טוב.

שאלה

בתרגיל 8 שאלה 2, האם מותר להשתמש במשפט הערך הממוצע, ואז להראות שזה פשוט לא יכול להיות a או b?

תשובה

לא כי זה פשוט לא נכון. קח את הפונקציה הקבועה. קח פונקציה אחרת שבמקרה מקבלת את הממוצע בקצוות...

(מישהו אחר) אני השתמשתי במשפט הערך הממוצע, ואז אמרתי שאם הנקודה מתקבלת בקצוות אז יש עוד נקודה, באמצע, בעלת אותו ערך...

איך זה נובע מכך שזה הערך באחד הקצוות, שזה גם הערך בנקודה באמצע?

הוכחתי את זה... בגדול הרעיון הוא שאם כל הנקודות באמצע היו מעל/מתחת לערך המבוקש אז מגיעים לסתירה, ומכאן ממשיכים עם ערך הביניים

אין לי מה להוסיף, אם הוכחת אז בסדר, אם טעית לא בסדר. זה בדיוק התרגיל... אני לא רואה שום שימוש במשפט ערך הממוצע.

שאלונת

האם אינטגרביליות של פונקציה בקטע [a,b] גוררת קיום של פונקציה קדומה בקטע זה? (ברור לי שההפך לא נכון, אבל בקשר לכיוון הזה אני לא בטוחה..)

תשובה

בוודאי שלא, כי יכול להיות שהאינטגרבילית מכילה אי רציפות סליקה או ממין ראשון ולכן אין לה קדומה. למשל פונקציה קבועה עם קפיצה בנקודה אחת, אין לה קדומה.

שאלה

ראיתי שבפתרון לתרגיל 6 שאלה 2 התשובה מבוססת על סכום דרבו עליון. האם זה בסדר שההוכחה שלי מבוססת על הטענה שאי-שוויון ברמת הפונקציות גורר אי-שוויון ברמת האינטגרל, (כמובן תוך שימוש באותה הנחה בפתרון שנתתם, ובכך שהיא מובילה לקיומה של סביבה בה הפונקצייה חיובית), כך שפרקתי את האינטגרל ל-3 אינטגרלים (שניים מחוץ לסביבה החדשה שבה הפונקצייה חיובית, ואחד בתוכה), ואם האינטגרל המקורי שווה לאפס, ושני האינטגרלים מחות לסביבה אי-שליליים, והאינטגרל בסביבה חיובי ממש, אז קבלנו ש- 0<0.

תשובה

נשמע תקין

שאלה

פונקציה לה יש מס' סופי של נקודות אי רציפות ממין ראשון היא אינטגרבילית. האם זה נכון לכל פונקציה שיש לה מס' סופי של נק' אי רציפות? (למשל סליקה או ממין שני)

== אם f(x)>=m>0 אז ברור שהאינטגרל של f(x) גדול מ0. אבל אם סתם ידוע שf(x)>0 בכל הקטע [a,b] אפשר לומר שהאינטגרל גדול ממש מ0 בקטע הזה?

תשובה

לפי משפט לבג פונקציה שקבוצת נקודות אי הרציפות שלה הן ממידה 0 (כלומר עוצמת א_0 או סופי) הינה אינטגרבילית, ללא קשר לסוג אי הרציפות.

עשינו את זה בכיתה. אם f>0 ואינטגרבילית, לפי לבג יש לה לפחות נקודת רציפות אחת. נניח שבנקודה הזו הערך של הפונקציה הינו m>0. לכן בסביבת דלתא הפונקציה גדולה מm/2 ולכן האינטרגל שם גדול מm/2 כפול דלתא וזה בוודאי גדול ממש מאפס.

אבל.. מספיק שתהיה לי נק' אי רציפות אחת ממין שני כדי שהפונקציה לא תהיה חסומה ולכן לא אינטגרבילית.

משפט לבג אכן מניח שהפונקציה תהיה חסומה. כעת, מי אמר שאי רציפות ממין שני גוררת אי חסימות? בוודאי זה לא נכון.

שאלה על הבוחן

האם יש בבוחן דף נוסחאות של האינטגרלים? תודה

תקרא את מה שתומר רשם למעלה

שאלה נוספת - האם מותר להשתמש במשפטים שהוכחנו בתרגיל? (למשל בתרגיל 7, שאלה 1 a)

אם אתה יודע לצטט נכון את המשפט, וברור שהוא לא עיקר התרגיל אז כן. אפשר גם לצטט דברים שעשינו בכיתה.

שאלה-תרגיל 7 שאלה 1 b

בתשובות כתוב ש-f לא בהכרח רציפה על כל הממשיים, אבל הדוגמה לא טובה. ה-f ששמתם לא רציפה עם מחזור 2 כמו שכתבתם: 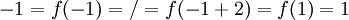$-1=f(-1)=/=f(-1+2)=f(1)=1$.

תשובה

צודק, טעות שלי, אני אפרסם תיקון לפתרון. הפונקציה כן רציפה בכל הממשיים כי בנקודות הבעיתיות מהצורה 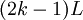$(2k-1)L$ הגבול מימין שווה לגבול משמאל שווה לערך הפונקציה בנקודה L.

שאלה - תרגיל 6, שאלה 4

מהו n? האם לכל x בוחרים n מתאים? בכל מקרה, איך אפשר בכלל להוכיח שהפונקצייה הזו מונוטונית עולה?

תשובה

לכל n טבעי אם x נמצא בתחום הרשום אזי ערך הפונקציה הוא כפי שרשום. זוהי כמובן פונקצית מדרגות.

תרגיל 8 שאלה 7

בסעיף 7b זו לא טעות? כי הגבול שם הוא שאפסילון שואף לאינסוף, ובתרגיל הם רוצים ל-0+..התשובה נכונה רק הגבול לא..

כן, סתם שגיאת דפוס.

שאלה - אינטגרביליות

תהי f אינטגרבילית בקטע I, ו-g רציפה בקטע I. האם הרכבה של g על f אינטגרבילית?

(לא ארז/תומר). כן.. לדוגמה, פונקצית הערך המוחלט

ברור, פשוט שאלתי את זה כי ראיתי שלפי מה שרוני לימד אותנו בהרצאה g צריכה להיות רציפה על הקטע (חשבתי שיכול להיות שלמילה על יש משמעות במובן של כיסוי)

לא מקשיבים בתרגיל? הרי פתרנו את זה בשיעור. כן ההרכבה אינטגרבילית

תרגיל שלא הבנתי

האם יש קדומה לפונקציה הבאה ב (אינסוף,0]?- כש X גדול מ0 זה אי בחזקת חצי וכש X=0 זה 0

(לא ארז/תומר) לא, כי הפונקציה אינה מקיימת את תכונת ערך הביניים. למשל, בקטע [0,1] מתקיים f(0)=0, f(1)=e^1/2 אבל אין x בקטע עבורו f(x)=1.

תודה=] ואם הפונקציה הייתה רק כש X גדול מ0 זה אי בחזקת חצי, אז כן הייתה קדומה?

שאלה

האם יהיה מותר מחשבון בבוחן? אנחנו מאוד נודה לכם אם כן. לעיתים יש חישובים קטנים שלעיתים נשכחים מהראש שלנו, למשל tan של ביטוי פשוט המכיל פאי וכו'.. בבוחן באינפי 1 למשל היה מחדל בעניין הזה.

יש לי הצעה (במקום מחשבון) - אולי יש אפשרות שאם מישהו במקרה שכח מה זה 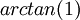$arctan(1)$, למשל, אז תהיה אפשרות שהמתרגלים בסביבה יוכלו לעזור לו?

תשובה

תראו, אתם בשלב הזה כבר צריכים לדעת את הדברים האלה לבד. אני לא בטוח אם יהיה מחשבון או לא, נחליט את זה בהמשך, אבל בכל מקרה אתם צריכים בהחלט לדעת לבד מה זה arctang(1). אתם צריכים לדעת מתי הסינוס עולה, מתי הוא יורד, מתי הוא שווה לקוסינוס, מתי הוא שווה 1 מינוס 1 וכו'.

אבל ארז, בשיא הכנות.. בזמן הבוחן אנחנו נורא לחוצים - הרוב המוחלט שלנו. לעיתים אנחנו שוכחים דברים קטנים מסוימים.. בתיכון היינו מורגלים לעבוד עם מחשבון וגם במהלך הסמסטר. זה לא דברים שקשורים לקורסים - אלו סתם דברים חישוביים.. זה נורא יקל עלינו אם תרשו לנו להשתמש במחשבון.. באמת שאני לא מבין איפה הבעיה. (לא מחשבונים משוכללים.. המחשבון הרגיל והפשוט..). מלבד העניין של הסינוסים - גם בפתירת אינטגרלים מסוימים מחשבון עשוי להקל. (בכל מיני חישובים מספריים שהאינטגרל המסוים דורש מאיתנו.. בשלב הסופי)

אני מבין שאתם לחוצים ושוכחים דברים, מתי לא שוכחים? כשמתרגלים מספיק. הרעיון הוא שאתם צריכים לדעת לחשב מספיק טוב מבלי לבדוק במחשבון. הנטייה באוניברסיטה (בניגוד לתיכון) היא לא להשתמש במחשבונים וכדי שתתרגלו לזה. יחד עם זאת, אני לא בטוח אם נאפשר או לא נאפשר מחר את השימוש במחשבון.

אפשר לפחות בבוחן הזה להתיר לנו להשתמש במחשבון? מאחרי הבוחן הזה אנחנו נתחיל לנסות להתרגל לשימוש בלי מחשבון אבל עד עכשיו התרגלנו לשימוש עם מחשבון ויום לפני הבוחן אנחנו לא יכולים לשנות שום דבר וזה סתם מביא לנו יותר לחץ.. אז אם אפשר, תתנו לנו בבוחן הזה שימוש במחשבון ואח"כ כבר נתחיל לנסות תרגיל בלי מחשבון.. תודה מראש!!

תומר - ארז היה מאוד סבלני איתכם אז אני אקח את תפקיד "הרע" כאן (טוב , אני לא ממש רע - זה הכל לטובתכם בסופו של דבר ...) - בכל אופן , האינטואיציה שאתם אמורים לפתח אמורה להיות זאת שבזכותה לא תזדקקו לשימוש במחשבון . ברור שמחשבון גרפי - שזה משהו שאם מישהו מכם ישתמש בו - יהיה יתרון על פני אחרים , אבל חיסרון גדול במבחן למי שהתרגל לעבוד איתו ... בקיצור - לדעת שסינוס של פאי / 6 זה חצי , למשל , זה משהו שאתם צריכים לדעת , ואל תשכחו - אתם לומדים מ ת מ ט י ק ה ! ויש דברים שטבועים בכם/מצופים מכם , בלי להזדקק למחשבון !

אבל ממש לא דיברנו על מחשבון גרפי. דיברנו על מחשבון פשוט ורגיל.. כדי שבמקום שנתעסק בחישובים פשוטים שהם כביכול מובנים מאליהם אבל לפעמים יכולים לגרום לטעויות שטויות שלא קשורות בכלל להבנתו של התלמיד בקורס הנלמד - נוכל להיעזר במחשבון לדברים, באמת, פשוטים.

תומר - בואו נהיה כנים עם עצמנו ונשאל - כמה כבר יצא לנו לעשות חישובים פשוטים בקורס ? כמה פעמים כפלתם שני מספרים בני יותר מ 5 ספרות כל אחד או נדרשתם לחשב בדיוק של 4 ספרות אחרי הנקודה ? - כמעט ולא היו ! אם הייתם צריכים לחשב חישובים כאלו - היינו מאפשרים שימוש במחשבון וכשאני כותב שאסור שימוש בכל חומר עזר , אפשר להסיק האם מצפים שתחשבו חישובים דוגמת זה בבוחן :) ב ה צ ל ח ה !

תומר- הנה דוגמא קלאסית: במבחן באינפי 1 היו כמה שאלות עם טריגונומטריה, והיו הרבה ילדים- והרבה זה לפחות 5-6, ששכחו את הזהויות(כלומר סינוסים, קוסינוסים וטנגטסים של פאי וכו'...) ואז שאלנו את המתרגל אם מה שחשבנו שזה זה נכון- והוא טעה- והטעה אותנו... אני באמת חושב שהוויכוח הזה על עם מחשבון או בלי פשוט מיותר- אם זה לא יכול לעזור מה אכפת לכם שנכניס?? זה הרי לא מה שאתם באים לבחון אותנו- באנו להיבחן באינפי..... תודה...

חבל שהמתרגל ענה לכם אם כך. מי ששוכח זהות טריגונומטרית - דינו לאבד נקודות. זה בהחלט חלק מהחומר שאתם צריכים לדעת, כמו שאני לא אעזור בציטוט משפטים מההרצאה. זה לא שמחשבון לא יכול לעזור - אנחנו לא מעוניינים שהוא יעזור לכם. גם פתרון מלא של הבוחן יעזור. אינפי כולל לדעת סינוסים.

שאלה - חילוף משתנה לאינטגרל

בעצם נוסחאת חילוף המשתנה באינטגרל מסוים היא בדיוק כמו שיטת ההצבה, רק שצריך להקפיד על כמה תנאים? (גזירות ברציפות של הפונקצייה שמציגה את x לפי t (שנסמנה ב-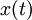$x(t)$), חסימות של 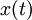$x(t)$ בין גבולות האינטגרצייה, ומוגדרות הפונקצייה 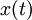$x(t)$ ב-a וב-b)

אני אוסיף שאלה נוספת - רק כדי להיות בטוח - באינטגרצייה בחלקים באינטגרל מסוים הדרישה היחידה היא גזירות ברציפות של f,g, נכון?

תשובה

לדעתי חילוף משתנה ושיטת ההצבה אלה שמות שונים של אותה שיטה (אני לא בטוח איך למדתם בהרצאה). התנאים שאמרת מספיקים אך לא הכרחיים. העיקר הוא שהפונקציה 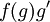$f(g)g'$ תהיה אינטגרבילית (אם מדובר על האינטגרל המסוים).

אם f וg גזירות ברציפות זה תנאי מספיק על מנת לשתמש באינטגרציה בחלקים.

בדף הנוסחאות שיהיה- תוכלו לשים את פולינום טיילור? הוא גם נוסחה.... ואילו עוד נוסחאות יהיו בו? ושל אילו אינטגרלים?תודה..

הכל במתמטיקה נוסחא. כמובן כמובן שאת פולינום טיילור אתם חייבים לתת לבד, זה לא יופיע בתור נוסחא. יהיו נוסחאות רלוונטיות שחשבנו שיעזרו לכן. אתם צריכים לזכור לבד גם נוסחאות טריגונומטריות.

שאלה

אני לא בטוח לגבי ההבנה שלי במשמעות של נק' קיצון ונק' פיתול, אשמח לבירור. נניח שאני מגדיר F להיות ב0 אפס, ובכל נק' אחרת x^2*sin 1/x. האם יש לF נק' קיצון? ופיתול?

תשובה

תבדוק אל מול ההגדרות:

• האם בסביבה (מנוקבת) של 0 כל הנקודות גבוהות מערך הפונקציה באפס? האם כולן נמוכות ממנו? (קיצון)

• האם הפונקציה גבוה מהמשיק בסביבה בצד אחד, ונמוכה מהמשיק בסביבה בצד השני? (פיתול)

איך אני כותב מתמטית שלא משנה כמה אני מתקרב ל0 תמיד יהיו יותר "פולסים" של הפונקציה ולכן זה לא קיצון\פיתול?

תנסה לחשוב לבד. מה השלילה של ההגדרות שרשמתי למעלה? תנסח את השלילה, ותדע איך מוכיחים מתמטית.

שאלה

צריך לזכור נגזרות של כל מיני פונקציות? כלומר, נגזרת של פולינום ופונקציה רציונלית כמובן שכן, אבל כל הפונקציות הטריגונומטריות וההיפרבוליות וההפוכות שלהן - הנגזרות שלהם נורא דומות ומאוד מבלבלות. עדיין נצטרך לזכור אותן?

מצטרף! אלו פונקציות שלא ראינו בתיכון, ותאמינו לי, שאת כל הנגזרות של הפונקציות הרציונליות אני יודע רק מהתיכון..... והצבות טיילור והצבות שפיתחנו.. (נגיד כשמציבים tg(x/2) אז הגענו למשהו שצריך להציב במקום הsin והcos..) נצטרך לזכור או שזה יהיה בדף נוסחאות?

תשובה

אתם צריכים לזכור (כי אתם תלמידי מתמטיקה ונשמח מאד אם נוסיף לכם ידע מעבר לתיכון). חוצמזה, כנראה שרוב הדברים הרלוונטיים יהיו בדף הנוסחאות. בלי קשר (או עם) חשוב לזכור נוסחאות טריגונומטריות שלא יהיו בדף הנוסחאות.

שאלה

בהצבות מסוג t=g(x) או x=g(t). באינטגרל הלא מסוים כאשר אני רוצה למצוא את הגבולות החדשים. אז בכל אחת מההצבות אני פשוט מחפשת את הt שעבורו t=g(a) וt=g(b) או במקרה השני a=g(t) או b=g(t)? כלומר.. אני תמיד מציבה את הגבולות המקוריים במקום הX ומחפשת את הt כדי להגיע לגבולות החדשים?

תשובה

כן משהו כזה. הגבולות החדשים הינם 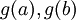$g(a), g(b)$ או $g^{-1}(a), g^{-1}(b)$

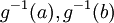
שאלה

מה הקטע שלכם?אתם מנסים להלחיץ בתקווה שככה נלמד יותר???????יש מאיתנו אנשים שרגישים ללחץ,לחץ סובב כבר את כל החיים שלנו,ואתם רק מוסיפים....מה יקרה אם תגידו מה מבנה הבוחן???אתם באמת חושבים שמישהו ילמד פחות טוב רק בגלל זה כשמדובר בפחות מיום לפני??? ומה יעזור אם נהיה בלי מחשבון?? אח"כ אתם טוענים שהבוחן לא דופק אותנו.... אני מצטער על הניסוח,ואני מעריך אתכם המתרגלים,אבל חאלאס עם השטויות!

תשובה

אנחנו יכולים לא להלחיץ אתכם בכך שנפסיק לענות, אל תגזימו.

נתנו מספיק מידע, מעכשיו כל אחד תלוי ביכולות האישיות שלו. מבחן הוא דבר מלחיץ במהותו, הדרך להתמודד איתו היא אישית. לנסות לקבל מידע עליו והקלות זה לא דרך להתמודד עם הלחץ. אנחנו עונים על שאלות על מנת שתוכלו ללמוד בצורה הטובה ביותר, ולא על מנת שתקבלו את הציון הגבוה ביותר.

לדעת את מבנה המבחן זה דבר בסיסי ביותר, גם לדעת מהם התנאים שיעמדו לרשותנו, אם זה מחשבון ואילו נוסאות לדעת ואילו לא.

יותר ברור: שום דבר לא בסיסי, בסיסי שתגיעו למבחן תעשו אותו ותקבלו ציון תוך שבועיים, השאר זה מותרות. מה לדעת? כל החומר עד ולא כולל אינטרגלים לא אמיתיים. בהצלחה.

אני דווקא חושבת שהמתרגלים עושים פה עבודה מצוינת. זה ממש לא מובן מאליו שיהיה פורום כזה, שנקבל בו מענה על כל שאלה קטנה שלנו (במהירות). אני גם חושבת שכדי להימנע מטעויות די מיותרות של חישובים פשוטים שלא קשורים בכלל לקורס, כדאי לתת להשתמש במחשבון אבל זו ההחלטה שלכם לגמרי.

שאלה

הבנתי שיהיו בבוחן תרגילים תיאורטיים. זה לא יהיה ברמה של להוכיח משפטים-משפטים מההרצאה נכון?..

תשובה

חיובי, כמו שאמרנו זה יהיה ברמת התרגיל - בית וכיתה (וגם בו היו שאלות תאורטיות)

אינטגרלים לא אמיתיים

היי. איך אפשר להוכיח שהאינטגרל הלא אמיתי (מa עד אינסוף) של sin^2 מתכנס? ניסיתי להראות בעזרת הגבול ופיתוח האינטגרל (ע"י זווית כפולה - cos2x=1-2sin(x)^2) אך יצא לי בכלל בדרך שכזו שהאינטגרל מתבדר...

(לא ארז/תומר) הטור אכן מתבדר... sin(x)^2 שווה למינוס חצי כפול cos(2x)-1. זוהי פונקציה מחזורית ולכן בוודאי מתבדרת. אולי התכוונת לאינטגרל sin(x^2) , שהוא מתכנס

תודה! רגע, אם יש לי משהו ששואף לאינסוף פחות משהו מתבדר, בוודאי אין גבול נכון? (כי זה למעשה 0.5x פחות sin(2x)/4, כאשר x שואף לאינסוף.. x הוא b לצורך העניין)

לא תמיד(רק כשהמתבדר לא שואף למינוס אינסוף אפשר להיות בטוחים). יותר נכון לומר שמשהו שואף לאינסוף פחות משהו חסום- מתבדר. אפשרות נוספת היא פשוט לומר שהאינטגרל מתבדר כי הפונקציה cos(2x)-1 מחזורית. אני לא יודע אם הנימוק הזה מתקבל, אבל אפשר להוכיח את זה בקלות.

שאלה 5

בבוחן בשאלה 5 לכולם יצא שישית או מינוס שישית אבל לי יצא אינסוף בדקתי במייפל ויצא לי אינסוף מישהו יכול לבדוק גם בשבילי ולהגיד לי אם צדקתי<?

בדקתי, יוצא מינוס שישית.

בטוח? גם אני ניסיתי עוד פעם זה מה שרשמתי והתשובה יוצאת אינסוף...limit((sin(sin(x))+sin(x))/x^3, x = 0) בעיקרון במבחן עשיתי לפי טיילור וגם יצא לי אינסוף

אחי במונה זה sin(sin(x))-sin(x)