אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות
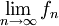
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
ארכיון
ארכיון 1 - תרגיל 1 ו2
ארכיון 2 - תרגיל 3
ארכיון 3 - תרגיל 3
ארכיון 4 - תרגיל 4
ארכיון 5 - תרגיל 4,5
ארכיון 6 - תרגיל 6
ארכיון 7 - (מי עוקב)
ארכיון 9 - לקראת הבוחן
שאלות
אינטגרלים לא אמיתיים
היי. איך אפשר להוכיח שהאינטגרל הלא אמיתי (מa עד אינסוף) של sin^2 מתכנס? ניסיתי להראות בעזרת הגבול ופיתוח האינטגרל (ע"י זווית כפולה - cos2x=1-2sin(x)^2) אך יצא לי בכלל בדרך שכזו שהאינטגרל מתבדר...
(לא ארז/תומר) הטור אכן מתבדר... sin(x)^2 שווה למינוס חצי כפול cos(2x)-1. זוהי פונקציה מחזורית ולכן בוודאי מתבדרת. אולי התכוונת לאינטגרל sin(x^2) , שהוא מתכנס
- תודה! רגע, אם יש לי משהו ששואף לאינסוף פחות משהו מתבדר, בוודאי אין גבול נכון? (כי זה למעשה 0.5x פחות sin(2x)/4, כאשר x שואף לאינסוף.. x הוא b לצורך העניין)
- לא תמיד(רק כשהמתבדר לא שואף למינוס אינסוף אפשר להיות בטוחים). יותר נכון לומר שמשהו שואף לאינסוף פחות משהו חסום- מתבדר. אפשרות נוספת היא פשוט לומר שהאינטגרל מתבדר כי הפונקציה cos(2x)-1 מחזורית. אני לא יודע אם הנימוק הזה מתקבל, אבל אפשר להוכיח את זה בקלות.
שאלה 5
בבוחן בשאלה 5 לכולם יצא שישית או מינוס שישית אבל לי יצא אינסוף בדקתי במייפל ויצא לי אינסוף מישהו יכול לבדוק גם בשבילי ולהגיד לי אם צדקתי<?
- בדקתי, יוצא מינוס שישית.
בטוח? גם אני ניסיתי עוד פעם זה מה שרשמתי והתשובה יוצאת אינסוף...limit((sin(sin(x))+sin(x))/x^3, x = 0) בעיקרון במבחן עשיתי לפי טיילור וגם יצא לי אינסוף
- אחי במונה זה sin(sin(x))-sin(x)
אפשר להעלות פתרונות לבוחן<?
כן נעלה אותם בקרוב. בינתיים בקצרה:
1. הפונקציה חיובית או שלילית בשני צדדי האינסוף, והיא חיובית וגם שלילית באיזור C כי היא לא קיצון
2. לנגזרת לא יכולים להיות יותר מ2 פתרונות, אבל צריכים היו להיות לפי רול אם היו יותר מ3 שורשים
4. משיעורי הבית (שני הסעיפים)
3. א. הצבה אוניברסלית. ב. הצבת x=sint ג. הצבה 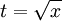
5. לופיטל - שישית או מינוס שישית (לא בדקתי עדיין)
6. הפרכה: פונקצית דיריכליי חסומה בין הקבועות אפס ואחד אך אינה אינטגרבילית
7. א. הוכחה (פשוט משפט ערך הממוצע)
7. ב. הוכחה (הקדומה תמיד רציפה, שווה לאפס באחד וגדולה מאחד ב2 ולפי ערך הביניים עוברת באחד)
8. נגדיר את הפונקציה 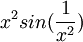 ונגדיר את הערך באפס להיות אפס. הפונקציה גזירה באפס וגם שלילית וגם חיובית בכל סביבה צדדית של אפס, לכן אין מינימום ואין מקסימום. המשיק הינו ציר x והפונקציה כאמור שלילית וחיובית ולכן לא רק מעל או רק מתחת ולכן אין גם פיתול. (מישהו שאל בדיוק את זה בפורום יום לפני הבוחן או משהו)
ונגדיר את הערך באפס להיות אפס. הפונקציה גזירה באפס וגם שלילית וגם חיובית בכל סביבה צדדית של אפס, לכן אין מינימום ואין מקסימום. המשיק הינו ציר x והפונקציה כאמור שלילית וחיובית ולכן לא רק מעל או רק מתחת ולכן אין גם פיתול. (מישהו שאל בדיוק את זה בפורום יום לפני הבוחן או משהו)
שאלה
אם רשמתי שיש לדירכלה אינסוף נקודות אי רציפות ולכן היא אינה אינטגרבילית כמה יורידו לי?
- 3 נקודות
בקשר לשאלה 1 בבוחן
כתבתם שp רציפה לחלוטין לכן בנק' קיצון מקומיות הנגזרת שלה מתאפסת. הנימוק לכך שהנגזרת שלה מתאפסת הוא לא העובדה שהיא גזירה בקטע הזה? (לפי פרמה) ולא רק רציפה.. (ברור שאם היא גזירה היא גם רציפה)
וגם בפיתרון לשאלה אחת. הוצאתם איקס בחזקת שני אן ואז נשאר לכם איכשהו איקס בתוך הביטוי,זה אמור להיות אחת חלקי איקס,לא?
תשובה
האמת שמספיק שהיא גזירה בנקודה...
כן.
אני אתקן
שאלה
בשאלה 4 ב', הוכחתי שפונקציית הערך המוחלט היא אינטגרבילית, אבל לא בדרך הפיתרון שרשומה באתר. (ראיתי את הפיתרון הזה, אבל רוני הוכיח בכיתה בדרך אחרת שהייתה יותר מובנת לי ולכן השתמשתי בה) הרעיון שהשתמשתי בו הוא זה שפונקציית הערך המוחלט חסומה (כי המקורית חסומה) ושבכל תת קטע, הסופרימום פחות האינפימום של פונקציית הערך המוחלט תמיד קטן מהסופרימום פחות האינפימום של הפונקציה הרגילה. אם ידוע שהסכום העליון פחות הסכום התחתון בפונקציה הרגילה קטן מאפסילון, אז כמובן שזה נכון גם לפונקציית הערך המוחלט מהסיבה הנ"ל.
האם הפיתרון נכון?
דרך אגב - אני חושב שבמקום לכתוב שהסופרימום של הערך המוחלט פחות האינפימום של הערך המוחלט, כתבתי הפוך: כלומר, הערך המוחלט של הסופרימום פחות הערך המוחלט של האינפימום. לכאורה זה משנה את ההוכחה ב-180 מעלות אבל זוהי טעות כתיבה ולא טעות של הוכחה.
מקווה שלא תורידו לי יותר מידי :)
- וואו סחטין על הפירוט, אבל בשביל זה יש את דף המבחן, תדע אחרי הבדיקה איך הלך :)
שאלה
היי, זה בקשר לאינטגרציה בחלקים. אם אני רוצה לעשות אינטגרציה בחלקים לאינטגרל של f כפול g (שימו לב: לא f כפול g' או f' כפול g, אלא רק f*g) מהם התנאים? שg תהיה רציפה (על מנת שתהיה לה קדומה) ומה עוד? האם נדרש משהו לגבי f?
תשובה
אתה יכול לענות על שאלות כאלה בעצמך. בואו נראה מה הנוסחא הסופית, ולכן מה התנאים שנגזרים ממנה. אתה רוצה לומר 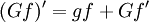 ואז לעשות אינטגרציה בשני הצדדים, ולכן האינטגרל צריך להיות מוגדר על כל הביטויים.
ואז לעשות אינטגרציה בשני הצדדים, ולכן האינטגרל צריך להיות מוגדר על כל הביטויים.
צריך שלg תהיה קדומה ושf תהיה גזירה, ושתהיה קדומה ל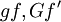 . להניח שכל הפונקציה בביטוי רציפות יעשה את הטריק למשל (כולל הנגזרת של f).
. להניח שכל הפונקציה בביטוי רציפות יעשה את הטריק למשל (כולל הנגזרת של f).