שיחה:88-222 תשעד סמסטר ב נוביק
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
המרחב 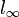
בתרגול האחרון הגדרנו את: 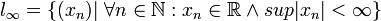
(דמיינו שיש מסביב להגדרה סוגריים מסולסלים, משום מה זה לא מצייר לי אותם. גם בכל ה-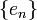 אמורים להיות סוגריים מסולסלים...)
אמורים להיות סוגריים מסולסלים...)
כלומר, 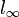 הוא מרחב של סדרות ממשיות חסומות.
הוא מרחב של סדרות ממשיות חסומות.
אחר כך הגדרנו סדרה 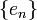 על ידי:
על ידי:
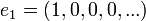
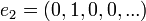
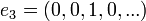 וכן הלאה.
וכן הלאה.
ואז התבקשנו להראות ש-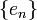 לא מתכנסת ב-
לא מתכנסת ב-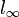 (למרות שהיא כן מתכנסת רכיב-רכיב).
(למרות שהיא כן מתכנסת רכיב-רכיב).
אבל, למיטב הבנתי, 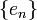 בכלל לא שייכת למרחב
בכלל לא שייכת למרחב 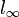 , כי איבריה לא ממשיים (לכל
, כי איבריה לא ממשיים (לכל 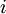 סדרת הרכיבים ה-
סדרת הרכיבים ה-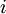 -ים היא ממשית, אבל
-ים היא ממשית, אבל 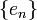 היא סדרה וקטורית). לא?...
היא סדרה וקטורית). לא?...
הערה לגבי הכתיבה המתמטית:
- שימו לב שהסינטקס של סימן השייכות הוא "in\"
- על מנת לעשות סוגריים מסולסלים בתוך הפורמט המתמטי, יש לשים לפניהם את הלוכסן: "{\"
--לואי (שיחה) 07:47, 9 במרץ 2014 (EDT)
אוקיי, הבנתי ואתה צודק. הסדרה לא צריכה להיות שייכת למרחב, אלא האיברים שלה.
אבל עכשיו יש לי שאלה נוספת...כל איבר (במרחב וכן בסדרה 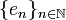 ) הוא סדרה או וקטור אינסופי. אז איך מוגדרת המטריקה במרחב? מה המרחק, נניח, בין
) הוא סדרה או וקטור אינסופי. אז איך מוגדרת המטריקה במרחב? מה המרחק, נניח, בין 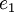 לבין
לבין 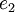 ?
?
- למעשה
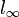 זו הקבוצה של הסדרות הממשיות החסומות עם נורמה ספציפית שהיא הסורפמום של הערכים המוחלטים של איברי הסדרה. תמיד כשנדבר על מטריקה בסיטואציה של מרחב נורמי נתכוון למטריקה המושרית מהנורמה. המרחק בין שני איברים הוא הנורמה של ההפרש. בוקטור
זו הקבוצה של הסדרות הממשיות החסומות עם נורמה ספציפית שהיא הסורפמום של הערכים המוחלטים של איברי הסדרה. תמיד כשנדבר על מטריקה בסיטואציה של מרחב נורמי נתכוון למטריקה המושרית מהנורמה. המרחק בין שני איברים הוא הנורמה של ההפרש. בוקטור 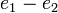 יש 1 ברכיב הראשון, מינוס 1 בשני ואפס בכל השאר. לכן הסופרמום של הערכים המוחלטים הוא 1. אם ממש רוצים לכתוב פורמלית כנראה שצריך לעבוד עם אינדקסציה כפולה-
יש 1 ברכיב הראשון, מינוס 1 בשני ואפס בכל השאר. לכן הסופרמום של הערכים המוחלטים הוא 1. אם ממש רוצים לכתוב פורמלית כנראה שצריך לעבוד עם אינדקסציה כפולה-
- למעשה
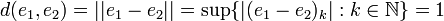 . באופן כללי לכל
. באופן כללי לכל  טבעי הרכיב הקיי של איבר
טבעי הרכיב הקיי של איבר
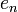 מקיים
מקיים 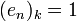 אם
אם 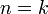 ואפס אחרת. כך גם אפשר להגיע ל
ואפס אחרת. כך גם אפשר להגיע ל
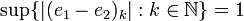 לפי מה שציינתי קודם. --מני (שיחה) 18:36, 9 במרץ 2014 (EDT)
לפי מה שציינתי קודם. --מני (שיחה) 18:36, 9 במרץ 2014 (EDT)
הבנתי. תודה!
עזרה בהוכחת כיוון במשפט מההרצאה
שלום.המרצה נתן משפט בו יש תכונות שקולות לגבי נקודות הצטברות. אחד מהכיוונים שהוא אמר להוכיח ואני לא בטוחה איך לעשות זאת זה כדלקמן:
"אם יש סדרת נקודות {x_n} שבה p לא מופיע וגם x_n->p אזי בכל סביבה של p יש אינסוף נקודות של A.
הנתונים הם:M מרחב מטרי ו-A מוכל ב-M. ובנוסף p שייכת ל-A
- כמה דברים שיכולים לעזור
- אני חושב שיש טעות בנתונים. הסדרה מוכלת בA והנקודה p שייכת ל-M ולא בהכרח ל-A.
- להשתמש בהגדרה של התכנסות דרך סביבות.
- קבוצה פתוחה פחות סגורה זה למעשה חיתוך של שתי פתוחות ולכן פתוחה.
- כל נקודון במ"מ הוא קבוצה סגורה וכנ"ל מספר סופי של נקודות.
- מחלק מהשלבים הקודמים נקבל שסביבה של נקודה p פחות קבוצה סופית של נקודות השונות מp גם היא סביבה של p. שוב אפשר להיעזר בשלב הראשון.
--מני (שיחה) 12:04, 18 במרץ 2014 (EDT)
דווקא אין טעות בנתונים.אתה יכול לראות זאת בהרצאה השנייה של ד״ר נוביק בדרופבוקס בגרסת PDF.
- קובץ שמועלה מן הסתם יכול להכיל טעויות וזה המקרה כאן. מה שטענתי הוא שלא צריך להניח שp שייכת ל-A ההוכחה עובדת בכל מקרה אם הנקודה בקבוצה או לא. לגבי מה שנאמר בהרצאה אני מניח שיש טעות כאן בקובץ עצמו. אם תסתכלי בסיכומי הרצאות מלפני שנתיים שהועלו לאתר תראי שp שייכת ל-M. ככלל נקודת הצטברות של קבוצה לא צריכה להשתייך לקבוצה.--מני (שיחה) 16:39, 18 במרץ 2014 (EDT)
תרגיל 2, שאלה 4
הסבר קצת יותר מפורט בשאלה 4 תרגיל בית 2:האם זה פשוט לקחת כל רכיב בסדרה ולמצוא לה סופרמום ואז זה הגבול? או שאולי אני מתבלבלת
תודה מראש
- תחילה שימי לב שבכל רכיב אין מדובר בסופרמום. למשל, ברכיב השלישי האיבר הראשון יהיה
 , שהוא יותר גדול מהגבול, ולכן הגבול הוא אינו הסופרמום.
, שהוא יותר גדול מהגבול, ולכן הגבול הוא אינו הסופרמום. - שימי לב שהתכנסות רכיב-רכיב אינה מספיקה להתכנסות. מצד שני, זה כן אפשרי להשתמש בגבול רכיב-רכיב על מנת לקבל אינטואיציה/לנחש את הגבול.
- הערה כללית: להבא נא להפריד שאלות שלא קשורות זו לזו. תודה :)
--לואי (שיחה) 11:41, 18 במרץ 2014 (EDT)
תרגיל 4 שאלה 2
הפרכה לשקילות א' וג':
R מ"מ, 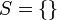
באופן ריק, כל סדרה 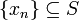 השואפת ל3 היא קבועה לבסוף.
השואפת ל3 היא קבועה לבסוף.
והרי 3 אינה שייכת לא לS ולא ל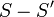
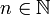 מתקיים
מתקיים 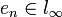 . תמיד כשמדברים על התכנסות של סדרה במרחב מטרי לנקודה אז הסדרה אמורה להיות מוכלת במרחב. אצלנו מדובר בסדרה של סדרות כי כפי שאמרת אכן כל איבר במרחב עפ"י ההגדרה הוא סדרה חסומה.--
. תמיד כשמדברים על התכנסות של סדרה במרחב מטרי לנקודה אז הסדרה אמורה להיות מוכלת במרחב. אצלנו מדובר בסדרה של סדרות כי כפי שאמרת אכן כל איבר במרחב עפ"י ההגדרה הוא סדרה חסומה.--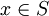 מה שאומר ש-
מה שאומר ש- אינה ריקה. --
אינה ריקה. --