89-214 סמסטר א' תשעא
מרצה (בשתי הקבוצות): פרופ' עוזי וישנה
מתרגלים (ארבע קבוצות): מיכאל פרידמן, דורון פרלמן
בחינות-עבר וחומר עזר נוסף אפשר למצוא באתר המרצה.
ראו גם:
- תמצית הקורס ותקצירי הרצאות
- דף תרגילים, כולל שאלות ותשובות
- דף משוב
דרישות קדם
דרישות הקדם הפורמליות הן קורס כלשהו באלגברה לינארית (88-112, 89-112 או 89-119), וקורס במתמטיקה בדידה (88-195 או 89-195).
אני מניח שאתם מכירים את המושגים הבאים (ואם לא, זה הזמן להשלים): קבוצה, תת-קבוצה, איחוד, חיתוך, יחס טרנזיטיבי, יחס סימטרי, יחס רפלקסיבי, יחס שקילות, יחס סדר חלש, מחלקת שקילות, פונקציה, פונקציה חד-חד-ערכית, פונקציה על, הרכבת פונקציות.
רשימת מושגים
במהלך הקורס נלמד מהם:
מחלק (ב-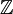
), חברות (ב-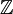), מחלק משותף מקסימלי, מנה ושארית (עדיין ב-ב-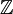), צירוף שלם, מספרים זרים, מספר ראשוני, מספר אי-פריק, פירוק לגורמים, חבורה למחצה, מונויד, איבר יחידה, איבר הפיך (במונויד), איבר הפכי (במונויד, בחבורה), מונויד עם צמצום, תת-חבורה, סדר של חבורה, חבורה ציקלית, חבורת אוילר, חבורה דיהדרלית, מכפלה ישרה חיצונית, קוסטים של תת-חבורה, החבורה הטריוויאלית, אינדקס של תת-חבורה, סדר של איבר, יוצר של חבורה ציקלית, קבוצת יוצרים של חבורה, מכפלה של תת-קבוצות בחבורה, תת-חבורות מתחלפות, היפוך של תת-קבוצה בחבורה, מכפלה של תת-חבורות, הומומורפיזם, אפימורפיזם, איזומורפיזם, אוטומורפיזם, גרעין, תמונה, תת-חבורה נורמלית, חבורת מנה, מרְכַז של חבורה, הצמדה, אוטומורפיזם פנימי, חבורת האוטומורפיזמים, מרכֵּז של איבר, מחלקת צמידות, החבורה הסימטרית מסדר n, תמורה, מחזור, חילוף, סימן, חבורת התמורות הזוגיות, חבורה פשוטה, מכפלה ישרה פנימית, נורמליזטור, קומוטטור, תת-חבורת הקומוטטורים, אקספוננט (של חבורה אבלית), צורה קנונית (של חבורה אבלית סופית); חוג, תת-חוג, חוג בלי יחידה, אידיאל שמאלי, אידיאל ימני, אידיאל (=אידיאל דו-צדדי), הומומורפיזם (של חוגים), תמונה, גרעין, חוג מנה, אידיאל ראשוני (בחוג קומוטטיבי), מחלקי אפס, תחום שלמות, חוג פשוט, אידיאל מקסימלי, חוג אוקלידי, מנה ושארית, אידיאל ראשי, חוג ראשי, איבר הפיך (בחוג), איבר ראשוני, איבר אי-פריק, תחום פריקות יחידה; פולינום אי-פריק, מימד של הרחבת שדות, שדה הרחבה ביחס לפולינום אי-פריק, מאפיין של שדה, חבורה כפלית של שדה.
