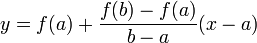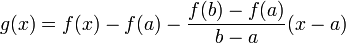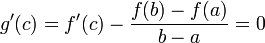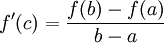משפט לגראנז' (אינפי)

משפט לגראנז'

תהי $f$ פונקציה רציפה בקטע $[a,b]$ וגזירה בקטע $(a,b)$ .

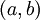אזי קיימת נקודה 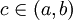$c\in (a,b)$ עבורה מתקיים $f'(c)=\dfrac{f(b)-f(a)}{b-a}$ .

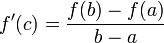הוכחה

נחשב את משוואת הישר העובר בין הנקודות 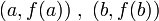$\big(a,f(a)\big)\ ,\ \big(b,f(b)\big)$ :

$y=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$

נחסיר את משוואת הישר הזה מהפונקציה המקורית, ונוכל להפעיל את משפט רול על-מנת לקבל את התוצאה הרצויה.

$g(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)$

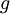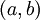$g$ רציפה ב- $[a,b]$ כהפרש פונקציות רציפות בקטע, וגזירה ב- $(a,b)$ כהפרש פונקציות גזירות בקטע.

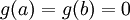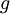קל לראות כי $g(a)=g(b)=0$ ו- $g$ . לכן לפי תנאי משפט רול קיימת נקודה 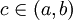$c\in(a,b)$ עבורה מתקיים $g'(c)=0$ .

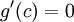אבל:

$g'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}=0$

כלומר

$f'(c)=\frac{f(b)-f(a)}{b-a}$

כפי שרצינו. $\blacksquare$

ראו גם

• משפט פרמה
• משפט רול