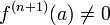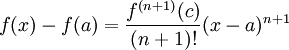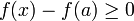סיווג נקודה חשודה
מתוך Math-Wiki
גרסה מ־12:40, 4 בנובמבר 2016 מאת יהודה שמחה (שיחה | תרומות)
הגדרת נקודה חשודה
תהי  פונקציה ממשית. נקודה
פונקציה ממשית. נקודה  בתחום ההגדרה של
בתחום ההגדרה של  נקראת חשודה אם
נקראת חשודה אם 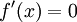 או שהנגזרת אינה מוגדרת ב-
או שהנגזרת אינה מוגדרת ב-  .
.
סיווג נקודות חשודות
משפט: תהי  פונקציה הגזירה ברציפות
פונקציה הגזירה ברציפות 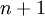 פעמים בסביבת הנקודה
פעמים בסביבת הנקודה  . עוד נניח כי
. עוד נניח כי
אזי:
- אם
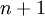 זוגי וגם
זוגי וגם 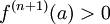 אזי
אזי  נקודת מינימום מקומי.
נקודת מינימום מקומי. - אם
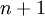 זוגי וגם
זוגי וגם 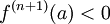 אזי
אזי  נקודת מקסימום מקומי.
נקודת מקסימום מקומי. - אם
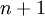 אי-זוגי אזי
אי-זוגי אזי  נקודת פיתול.
נקודת פיתול.
הוכחה:
לפי טיילור לכל  בסביבה קיימת נקודה
בסביבה קיימת נקודה 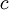 בין
בין  לבין
לבין  כך ש:
כך ש:
אבל לפי ההנחה כי  הנגזרות הראשונות מתאפסת ב-
הנגזרות הראשונות מתאפסת ב-  , מתקיים
, מתקיים
לכן, אם 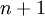 זוגי וגם
זוגי וגם 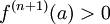 לפי רציפות הנגזרת השניה קיימת סביבה של
לפי רציפות הנגזרת השניה קיימת סביבה של  בה
בה 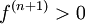 ולכן לכל
ולכן לכל  בסביבה זו מתקיים:
בסביבה זו מתקיים:
שכן 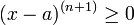 תמיד עבור
תמיד עבור 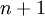 זוגי.
זוגי.
כלומר אם 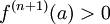 אזי
אזי  הנה נקודת מינימום.
הנה נקודת מינימום.
באופן דומה, אם 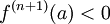 אזי
אזי  הנה נקודת מקסימום.
הנה נקודת מקסימום.
אם 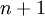 אי-זוגי, אזי הסימן של
אי-זוגי, אזי הסימן של 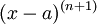 חיובי בסביבה ימנית של
חיובי בסביבה ימנית של  ושלילי משמאלה.
ושלילי משמאלה.
כיון שסימן 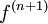 קבוע בסביבה של
קבוע בסביבה של  , סה"כ מצד אחד
, סה"כ מצד אחד 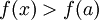 ומהצד השני
ומהצד השני 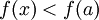 .
.
אבל הנגזרת הראשונה מתאפסת ב-  ולכן המשיק הוא
ולכן המשיק הוא 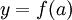 , ולכן הפונקציה קטנה ממנו בצד אחד וגדולה ממנו בצד השני ולכן
, ולכן הפונקציה קטנה ממנו בצד אחד וגדולה ממנו בצד השני ולכן  הנה נקודת פיתול.
הנה נקודת פיתול.