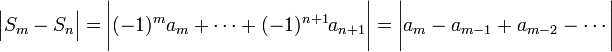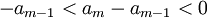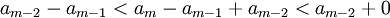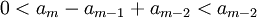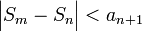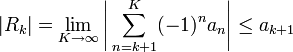משפט לייבניץ

משפט לייבניץ לטורים עם סימנים מתחלפים

תהי 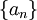$\{a_n\}$ סדרה חיובית, מונוטונית, השואפת לאפס. אזי:

• הטור 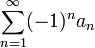$\sum\limits_{n=1}^\infty (-1)^na_n$ מתכנס
• השארית $R_k=\sum\limits_{n=1}^\infty (-1)^na_n-\sum\limits_{n=1}^k (-1)^na_n$ מקיימת $|R_k|\le a_{k+1}$

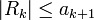
הוכחה

נוכיח כי סדרה הסכומים החלקיים של הטור הנה סדרת קושי, ועל כן הטור מתכנס.

יהי 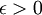$\epsilon>0$, צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני איברים קטן מ- $\epsilon$.

• $\Big|S_m-S_n\Big|=\Bigg|(-1)^ma_m+\cdots+(-1)^{n+1}a_{n+1}\Bigg|=\Bigg|a_m-a_{m-1}+a_{m-2}-\cdots\Bigg|$

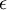נראה כי כל איבר "בולע" את קודמיו, לפי המונוטוניות של הסדרה:

$-a_{m-1}<a_m-a_{m-1}<0$

לכן

$a_{m-2}-a_{m-1}<a_m-a_{m-1}+a_{m-2}<a_{m-2}+0$

כלומר

$0<a_m-a_{m-1}+a_{m-2}<a_{m-2}$

וכן הלאה עד שנקבל

$\Big|S_m-S_n\Big|<a_{n+1}$

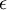וכיון ש$a_n$ שואפת לאפס, החל ממקום מסויים זה קטן מ- $\epsilon$ (ללא תלות ב- $m$).

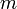לפי טיעון דומה, $\Bigg|\sum\limits_{n=k+1}^K (-1)^na_n\Bigg|=\Bigg|a_{k+1}-a_{k+2}+a_{k+3}-\cdots\Bigg|\le a_{k+1}$ ולכן

$|R_k|=\lim_{K\to\infty}\Bigg|\sum\limits_{n=k+1}^K (-1)^na_n\Bigg|\le a_{k+1}$

כפי שרצינו. $\blacksquare$