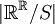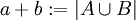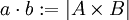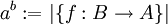88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 7
אריתמטיקה של עוצמות
תרגיל. יהיו A,B קבוצות כך ש, עוצמת B גדולה מאחד. הוכח כי העוצמה של אוסף הפונקציות מA לB גדולה מעוצמת A.
פתרון.
קל לבנות פונקציה על מאוסף הפונקציות מA לB אל A. נשלח כל פונקציה באוסף למקור של איבר b מסוים. מכיוון שכל הפונקציות מA לB נמצאות באוסף, בפרט כל הפונקציות ששולחות כל איבר מA ל-b יהיו שם.
נניח בשלילה שקיימת התאמה חח"ע ועל בין A לבין אוסף הפונקציות הנ"ל. נסמן ב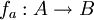 את הפונקציה המתאימה לאיבר
את הפונקציה המתאימה לאיבר  .
.
ידוע לנו שבקבוצה B יש לפחות שני איברים, לכן בהנתן אחד מהם אפשר לבחור את השני. נגדיר פונקציה באופן הבא 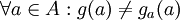 . לפי ההגדרות פונקציה זו הינה פונקציה מA לB אך אינה מתאימה לאף איבר בA בסתירה.
. לפי ההגדרות פונקציה זו הינה פונקציה מA לB אך אינה מתאימה לאף איבר בA בסתירה.
תרגיל. הוכח שעוצמת קבוצת החזקה של A תמיד גדולה מעוצמתה של A
הוכחה. קל להראות שקיימת העתקה חח"ע ועל בין אוסף הפונקציה 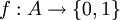 (כל קבוצה חלקית אומרת בעצם על כל איבר של A אם הוא שייך (1) או לא שייך (0). למשל הפונקציה המתאימה לקבוצה הריקה היא פונקצית האפס, והפונקציה המתאימה לקבוצה כולה היא הפונקציה 1).
(כל קבוצה חלקית אומרת בעצם על כל איבר של A אם הוא שייך (1) או לא שייך (0). למשל הפונקציה המתאימה לקבוצה הריקה היא פונקצית האפס, והפונקציה המתאימה לקבוצה כולה היא הפונקציה 1).
פונקציה זו עומדת בתנאי התרגיל לעיל ולכן עוצמתה גדולה מעוצמת A אבל זהה לעוצמה של קבוצת החזקה, כפי שרצינו.
הערה: מסיבה זו אוסף העוצמות אינו קבוצה אלא מחלקה. שכן אם הוא היה קבוצה, הייתה לו עוצמה
הגדרה:
יהיו שתי קבוצות A,B כך ש 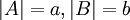 . אזי נגדיר פעולות בין עוצמות:
. אזי נגדיר פעולות בין עוצמות:
בהרצאה תוכיחו שהגדרות אלה מוגדרות היטב, כלומר העוצמה נשארת זהה ללא תלות בבחירת הקבוצות המייצגות.
שימו לב: מתוך הגדרה זו קל לראות את חוקי החזקות למקרי הקצה:
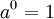 שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.
שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.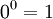 זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים
זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים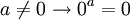 אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
תכונות האריתמטיקה
בהנחת אקסיומת הבחירה:
- אם a או b מייצגים עוצמה אינסופית אזי
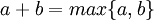
- אם a או b מייצגים עוצמה אינוספית ושניהם אינם אפס אזי
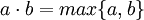
- אם
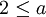 ו
ו 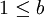 ולפחות אחת מבינהם הוא אינסופי אזי
ולפחות אחת מבינהם הוא אינסופי אזי 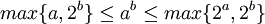
תרגיל ממבחן תשע מועד א (שי סרוסי ואפי כהן)
יהי S יחס על 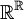 (קבוצת כל הפונקציות הממשיות), המוגדר על ידי
(קבוצת כל הפונקציות הממשיות), המוגדר על ידי 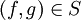 אם"ם לכל
אם"ם לכל 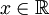 מתקיים
מתקיים 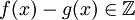
1. הוכיחו שS הינו יחס שקילות
2. תהי 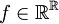 מצאו את
מצאו את ![|[f]|](/images/math/0/1/3/01364e045ffa77dc9f947de382b72c71.png)
3. מצאו את