אינפי 1 לתיכוניסטים תש"ע

אינפי 1 לתיכוניסטים

כאן יהיה המקום שלנו להיעזר אחד בשני בקורס חשבון אינפיניטסימלי 1. אתם מוזמנים לשאול שאלות ולדון בבעיות הנוגעות לקורס אינפי 1 - סטודנטים הלומדים בשתי הקבוצות מוזמנים להגיב כאן.

ארכיון

ארכיון 1

תרגילים + פתרונות

מדיה:09Infi1_Sol1.pdf: תרגיל 1

מדיה:09Infi1_Sol2.pdf: תרגיל 2

מדיה:09Infi1_Sol3.pdf: תרגיל 3

מדיה:09Infi1_Sol4.pdf: תרגיל 4

מדיה:09Infi1_Sol5.pdf: תרגיל 5

מדיה:09Infi1_Sol6.pdf: תרגיל 6

מדיה:09Infi1_Sol7.pdf: תרגיל 7

מדיה:09Infi1_Sol8.pdf: תרגיל 8

מדיה:09Infi1_Sol9.pdf: תרגיל 9

שאלות

שאלה

אני לא בטוח במשהו: במבחן ד'אלמבר , כתוב במייזלר שהטור מתבדר אם החלוקה גדולה או שווה ל 1. אני זוכר שהמתרגל פעם קיבל שהחלוקה שווה ל 1 אבל אמר שזה לא אומר כלום. אז מה נכון?

תשובה

אני אסביר. אם 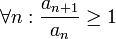$\forall n : \frac{a_{n+1}}{a_n}\geq 1$ זה אומר שהסדרה מונוטונית עולה. מכיוון שהיא חיובית, זה אומר שהיא בהכרח לא שואפת לאפס ולכן הטור מתבדר.

לעומת זאת, אם 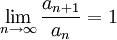$\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=1$ לא ניתן לדעת אם הטור מתכנס, משמע יש דוגמאות לשני הכיוונים. הטור ההרמוני 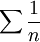$\sum \frac{1}{n}$ מקיים את התכונה הזו ומתבדר, ואילו הטור 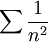$\sum \frac{1}{n^2}$ מקיים את התכונה הזו ומתכנס ($\lim_{n\rightarrow \infty}\frac{n^2}{(n+1)^2}=1$)

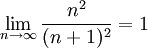שאלה

איך אני מראה שלמשוואה tg x = x יש אינסוף פתרונות ממשיים?

תשובה

$\lim_{x\rightarrow \frac{\pi}{2} +\pi k}tgx - x= \lim_{x\rightarrow \frac{\pi}{2} +\pi k}\frac{sinx}{cosx} - x = \pm \infty$

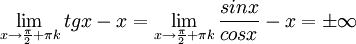
ולכן לפי משפט ערך הביניים כל ערך ממשי מתקבל בין השאיפה לאינסוף ומינוס אינסוף, וזה קורה אינסוף פעמים (לכל k). בפרט, 0 מתקבל אינסוף פעמים, ולכן 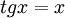$tgx=x$ אינסוף פעמים.

שאלה

האם פונ' חח"ע ועל היא מונוטונית?

תשובה

רציפה או לא? קח את x על הרציונליים, ו2x על האי רציונליים, חח"ע ועל ואינה מונוטונית.

אם היא רציפה, היא חייבת להיות מונוטונית לפי משפט ערך הביניים (תרגיל) ואפילו לא צריך את העל.

שאלה

נניח שיש לי פונקצייה שמוגדרת בתחום x>a, ובדיוק בנק' x=a יש אי-רציפות בצורה של 'אסימפטוטה' - האם זו אי רציפות מסוג ראשון, או שני?

תשובה

מה זה צורה של אסימפטוטה. ההגדרה מאד מאד פשוטה:

אי רציפות סליקה: קיים גבול סופי בנקודה

אי רציפות ממין ראשון: קיימים גבולות חד צדדיים סופיים בנקודה

אי רציפות ממין שני: כל מצב אחר

הדבר היחיד שאני לא בטוח לגביו, באמת בהקשר השאלה שלך, הוא מה קורה כאשר מדברים על פונקציה בתחום הגדרה מסוים. כלומר, מה היא האי רציפות של פונקציה 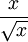$\frac{x}{\sqrt{x}}$ בנקודה אפס. מצד אחד לפי ההגדרה שרשמתי למעלה זה מין שני כי לא קיים הגבול החד צדדי משמאל. מצד שני, אם נחליף את הנקודה ב0 נקבל פונקציה רציפה ב(אינסוף,0], אז זה נשמע כמו סליקה. אז אני באמת לא בטוח מה ההגדרה במקרה כזה.