אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות
תוכן עניינים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
ארכיון
ארכיון 1 - תרגיל 1 ו2
ארכיון 2 - תרגיל 3
ארכיון 3 - תרגיל 3
שאלות
האם יש טעות בתרגיל 4ד?
בפונ' שבתרגיל 4ד' (בתרגיל שפורסם השבוע) המכנה והמונה שווים, מה שיוצא שצריך לעשות אינטגרל של 1dx פשוט. יכול להיות שיש שם טעות?
תשובה
שאלה
שאלה 5: לא פשוט מציבים במקום T את ההפוכתה לפיי על T?
- ומה עושים עם
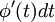 ? מחליפים בdx? למה מותר לעשות את זה? זה מה שצריך להוכיח...
? מחליפים בdx? למה מותר לעשות את זה? זה מה שצריך להוכיח...
שאלה
תומר אמר לנו בקבוצת תרגול שלו (יום ראשון) שבגלל שהתרגול היה קצר ולא הספקנו הכל-הוא ידחה לנו חלק מהתרגילים. אילו תרגילים קבוצת התרגול שלו לא צריכה לעשות השבוע?
שאלה
שלום תומר, זה רועי עסיס ועדי איקן מקבוצת התרגול שלך. רק רצינו להזכיר לך שדחית לנו את התרגיל הקרוב לשבוע הבא תודה רבה
שאלה
ב1)ב., האם יש להתייחס גם למקרה של קבוע האינטגרציה או שיש להוכיח\להפריך עד כדי קבוע?
תשובה
פונקציות קדומות יש הרבה. אם הנגזרת של F הינה f אזי F קדומה לf.
שאלה
מישהו יודע מתי מתחיל בדיוק הסמסטר קיץ??
זה ממש דחוף אז בבקשה תענו מהר...
- כמעט בטוח שהראשון לאוגוסט.
תרגיל 4 שאלה 2
הפונקציה max(x,x^2) הכוונה לפונקציה שבין 0 ל-1 שווה X ובכל השאר שווה X בריבוע? אם אני מגיע מתוך הרציפות של הפונקציה הקדומה ליחס מסוים בין קבועים בנקודה 1 ואח"כ אני גוזר בנקודות האלו ויוצא לי שהנגזרות החד צדדיות שוות אבל לא שוות ל 1 (כפי שMAX שווה בנקודה הזאת). יש דרך לתקן את הקדומה שתתאים לMAX הוא שזה גורר שלMAX אין קדומה?
תשובה
מה לגבי השליליים?
שנית, אתה בוחר פונקציה כך שהנגזרת שלה תהיי max ואז אתה מוסיף קבועים על מנת שתהיה רציפה. אבל הוספת קבועים לא משנה את הנגזרת, איך יכול להיות שהנגזרת היא לא אחד? זה קורה אם מראש בחרת אותה לא טוב, או שיש טעות חישוב.
שאלה
באחת ההרצאות מיכאל השתמתש בהצבה: 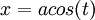 כדי לפתור את
כדי לפתור את 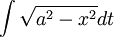 . הבעיה שבהצבה הזאת אנו מוכרחים להניח ש:
. הבעיה שבהצבה הזאת אנו מוכרחים להניח ש: 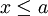 (כי
(כי 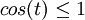 )וזה לא בהכרח נכון...
)וזה לא בהכרח נכון...
תשובה
האם הפונקציה 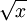 מוגדרת עבור
מוגדרת עבור 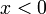 ?
?
שאלה
יש סיכוי שב2 אין בכלל קדומה? עשיתי בערך את מה שתומר עשה בכיתה, והגעתי לסתירה לגבי הקבועים - לא קיימים קבועים בכלל.
תשובה
יש 2 נקודות בעייתיות, ויש שלושה קבועים שניתן לבחור באופן חופשי. זה 2 משוואות ב3 נעלמים. איך נוצרת סתירה?
- איך שלושה קבועים?
- כמה נקודות 'בעייתיות' יש?
- לא משנה, הבנתי, תודה רבה :)
- כמה נקודות 'בעייתיות' יש?
שאלה
היי ארז, בתרגול האחרון ההספק היה ממש מועט בגלל שזה היה ערב יום השואה. ביום ראשון ההספק גם יהיה מועט כי זה ערב יום הזיכרון. האם נשלים את החומר מתישהו? יש הרבה דוגמאות שלא ראינו, שמופיעות בתרגילי הבית...
תשובה
תרגיל הבית נכתב בהתאם להספק בשיעור, אם יש דוגמא שלא ראיתם אתם אמורים להתמודד איתה לבד. כך גם יהיה בראשון הקרוב..
בנוסף יתפרסמו פתרונות לתרגילים שניתן ללמוד גם מהם.
שאלה
כשצריך למצוא נוסחא רקורסיבית, עבור איזה m לחשב את תנאי העצירה? חישבתי עבור m=0, האם זה מספיק?
תשובה
אם הנוסחא נכונה עבור m=0 ואפשר ממנה להסיק את שאר המקרים זה בסדר. אם לא אז לא. כלומר, תנסה להגיע מאפס לאחד בעזרת הנוסחא
שאלה
זה נכון להגיד שלפונ' לא רציפה אין פונ' קדומה? כי אז הנגזרת של הפונ' הקדומה לא רציפה ולכן היא בעצם לא גזירה בכל הנקודות?
תשובה
לא. אין חוק שאומר שנגזרת חייבת להיות רציפה, אחרת להגדרה גזירה ברציפות לא הייתה משמעות.
לדוגמא:
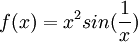 ונגדיר
ונגדיר 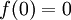 . ברור שהפונקציה גזירה בכל נקודה פרט לאפס, נבדוק מה קורה בנקודה אפס עצמה:
. ברור שהפונקציה גזירה בכל נקודה פרט לאפס, נבדוק מה קורה בנקודה אפס עצמה: 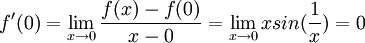
לכן הפונקציה גזירה בכל מקום. נבדוק האם הנגזרת רציפה:
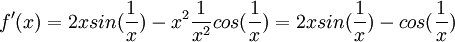
קל לראות שלא קיים הגבול 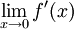 ולכן בוודאי
ולכן בוודאי 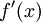 אינה רציפה באפס.
אינה רציפה באפס.
אבל יש לה קדומה, f+C.
שאלה
האם בשאלה 2 אפשר להניח קיום של פונקציה קדומה, ואז למצוא את ערכיה על כל הממשיים?
תשובה
אני לא בטוח לגמרי מה הכוונה אבל אני אענה בכלליות. מותר במתמטיקה לבצע איזה הנחות משוגעות שאתה רוצה על מנת להגיד לפתרון, כל עוד בסופו של דבר אתה מוכיח שהוא אכן הפתרון. מה הכוונה? אתה יכול להגדיר את הפונקציה הקדומה איך שאתה אבל בסוף אתה צריך להוכיח שהנגזת של הפונקציה שמצאת היא אכן הפונקציה הנתונה.
אסור להניח שיש קדומה ורק להגיד מה הערך שלה מבלי להוכיח שהיא אכן הקדומה על ידי גזירה.
שאלה
בתרגיל 5 צריך להשתמש במשפט מאינפי 1 על נגזרת של פונקציה הפוכה:
אם f גזירה והפיכה, ו 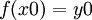 , ו
, ו 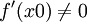 , אז
, אז
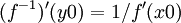 .
איך נדע בתרגיל שאכן הנגזרת שונה מאפס, כדי שנוכל לחלק בה?
.
איך נדע בתרגיל שאכן הנגזרת שונה מאפס, כדי שנוכל לחלק בה?
- מישהו?
- מצטרפת לשאלה
- אפשר לקבל איזושהי תשובה? ההגשה היום..
- מצטרפת לשאלה
תשובה
יש שתי שיטות לפתור את התרגיל. באחת מהן אין צורך לגזור את ההפוכה כלל (זו הדרך הקצרה יותר)
אם אתם כן גוזרים, תניחו שהיא שונה מאפס. תחשבו על זה שאם הנזרת שווה לאפס בכמה נקודותבודדות אז מקסימום קיבלתם קדומה בכל נקודה אחרת. והנגזרת לא יכולה להתאפס על קטע שלם כי אז 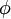 תהייה קבועה ולא חח"ע. אבל כמו שאמרתי, לא חייבים לגזור.
תהייה קבועה ולא חח"ע. אבל כמו שאמרתי, לא חייבים לגזור.
- אבל זה בעצם אומר שהטענה הזאת לא ב-100% נכונה, קיבלנו פונקציה קדומה רק בנקודה שבהן הנגזרת אינה אפס.
המשך תשובה
כפי שהראתי היום בכיתה, ידוע בתרגיל ש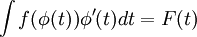 נבצע את ההצבה
נבצע את ההצבה 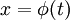 ולכן
ולכן 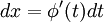 ולכן
ולכן
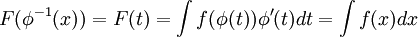
עכשיו, מדוע אסור היה לנו פשוט לגזור את 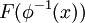 ? כי כאשר אנחנו גוזרים לפי הרכבה אנחנו מניחים ששתי הפונקציות גזירות (זו הנחה של הוכחת הנוסחא של גזירת הרכבה) ולכן כאשר הפונקציה
? כי כאשר אנחנו גוזרים לפי הרכבה אנחנו מניחים ששתי הפונקציות גזירות (זו הנחה של הוכחת הנוסחא של גזירת הרכבה) ולכן כאשר הפונקציה 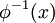 אינה גזירה, לא ניתן לדעת מה הנגזרת של
אינה גזירה, לא ניתן לדעת מה הנגזרת של 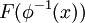 (בהחלט לא ניתן לאמר שהיא אינה גזירה).
(בהחלט לא ניתן לאמר שהיא אינה גזירה).
לדוגמא, ניקח 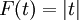 ,
, 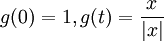 .
לכן,
.
לכן, 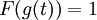 והנגזרת שלו היא בוודאי אפס. אבל לא ניתן לאמר שהנגזרת שווה ל
והנגזרת שלו היא בוודאי אפס. אבל לא ניתן לאמר שהנגזרת שווה ל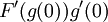 מכיוון שg איננה גזירה כלל באפס.
מכיוון שg איננה גזירה כלל באפס.