אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות

$\lim_{n\rightarrow\infty}f_n$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - תרגיל 1 ו2

ארכיון 2 - תרגיל 3

ארכיון 3 - תרגיל 3

ארכיון 4 - תרגיל 4

ארכיון 5 - תרגיל 4,5

ארכיון 6 - תרגיל 6

ארכיון 7 - (מי עוקב)

שאלות

השאלה שרוני ביתן נתן בתאריך ה2/5 ופתרונה

f רציפה, מחזורית ואי שלילית(אינה זהותית 0) ב-R =>? האינטגרל שלה מתבדר באינסוף.

פתרון: הפיתרון נעשה יחסית פשוט מאז שהועלה תרגיל 7(שאלה 1 ב' עוזרת) [[1]]

השאלה היתה להוכיח שהאינטגרל של: f(x)/x מתבדר... ההוכחה שהוכחת היא טריוויאלית: נניח שאחרי אורך מחזור האינטגרל על הפונקציה הוא I. אזי ברור שאם ניקח אינטגרל על הפונקציה לאורך M/I האינטגרל יהיה שווה M (כי הפונקציה מחזורית) וb שואף לאינסוף ולכן גם האינטגרל.

שאלה - פונקציות טריגונומטריות ממעלה גבוהה

נניח שאני רוצה לחשב את האינטגרל של סינוס בחמישית של x. האם "חוקי", בהנחה שהצבתי 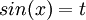$sin(x)=t$, להסיק ש: 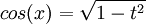$cos(x)=\sqrt{1-t^2}$ להמשך ההצבה? אם לא, באילו דרכים נוספות (מלבד ההצבה האוניברסאלית שלא נראית יעילה במיוחד והנוסחא לחישוב סינוס ממעלה גבוהה) ניתן לחשב את האינטגרל?

הערה : שמתי לב שמאחר וחזקת הסינוס היא אי-זוגית, נוח יותר להציב t=cosx. אני ממשיך לשאול את אותה שאלה באופן כללי.

תשובה

מוצאים את פיתרון האינטגרל על ידי הנוסחא הרקורסיבית: [[2]]

אם אתה צריך לחשב את האינטגרל של cos(x( ממעלה מסויימת אתה יכול להמיר אותו לאינטגרלים של sin(x) או שאתה יכול להשתמש בנוסחא: [[3]]

שאלה בקשר לבוחן

מה יהיו הנושאים בבוחן? איזה סוג של שאלות הוא יכלול? עברתי על כל התרגילים שנתנו עד כה (1-8), החל ממשפטי לגראנז' והערך הממוצע, דרך כלל לופיטל, חקירת פונקציות, טורי טיילור, עד לאינטגרלים הלא מסויימים, הצבות שונות, ולבסוף את כל הנושא של האינטגרביליות ועד לחישובים השונים של אינטגרלים מסויימים. אני די מתוסכל כי זה המון חומר ואשמח אם תוכלו לספק מידע, אפילו מועט, בנוגע לסוג השאלות שיופיעו בבוחן : האם תהיה בחירה? האם יהיו שאלות מסוג אמריקאי / נכון לא נכון? הוכח או הפרך? האם נצטרך לחקור פונקציות? תודה!

תשובה

ציינת יפה את רשימת החומר לבוחן.

יהיו שאלות הוכחה כלומר שאלות תאורטיות, ויהיו שאלות קצרות יותר בסגנון של הוכח הפרך (עם תשובה קצרה). צריך לדעת חקירת פונקציות, אבל לא נתן לכם לחקור פונקציה מלאה.

ותהרגו אותי אם אני מבין איך עוזר לכם לדעת אם תהיה בחירה או לא. אם המטרה היא לדלג על חומר מסוים מתוך ההנחה שתוכל לבחור לא לענות על שאלות בנושא, אני ממליץ לא לעשות את זה (כנראה שלא תהיה בחירה, וגם אם כן לא נאפשר לבחור בין נושאים שונים)

הסיבה היא בעיקר להרגיע אותנו - יהיה לך קשה למצוא סטודנטים רציניים שלא לחוצים מהבוחן הקרוב. אח"כ, המטרה שלשמה שאלתי את השאלה היא כדי לנסות ולמקד את תהליך הלמידה - בבחנים משנים קודמות קשה מאוד למצוא שאלות 'תאורטיות' או שאלות מסוג 'הוכח או הפרך', כך שמלבד חישוב אינטגרלים, חקירת פונקציות וחזרה עמוקה על החומר והתרגילים אין יותר מדי דרכים להתכונן לבוחן...

אם תדע לפתור תרגילים כמו בתרגילי הבית מצבך יהיה טוב.

לקראת הבוחן

יש מצב שיועלו לאתר בחנים לדוגמא / שאלות לתרגול?

תשובה

אולי יעלו שאלות לדוגמא, בינתיים תרגילי הבית הם הדוגמאות (והתרגילים שביצענו בכיתה)

תרגיל 8 שאלה 6

אם אני אקח f(x)= 1/delta כאשר X=0 ואחרת f(x)= x/sin(x*delda אז f גזירה ברציפות ועונה על נתוני השאלה אך הגבול שמופיע בשאלה אינו שווה ל-0 כאשר ניקח למשל גבולות אינטגרציה מ-2 ל-1. אז איך מוכיחים דבר שניתן להפרכה?

תשובה

מה זאת אומרת 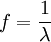$f=\frac{1}{\lambda}$? זה אומר למעשה שאתה משנה את f יחד עם הגבול. אבל f הינה פונקציה של x בלבד, היא לא אמורה להשתנות לפי $\lambda$.

שאלה

$\lambda$ זה לא סקלאר?

זה לא לינארית, מה זה אומר סקאלר? הוא משתנה גם כן, ועליו אנחנו לוקחים את הגבול. f הינה פונקציה של המשתנה x ואילו האינטגרל המסויים הינו פונקציה של המשתנה $\lambda$. לכן אפשר לקחת את הגבול של הפונקציה הזו באינסוף

תרגיל 9

גם השבוע לקבוצה שמתרגלת בימי ראשון יהיה תרגיל נוסף, ולקבוצה השנייה לא, כתוצאה מחג שבועות. למתרגלים של הקבוצה הראשונה - ארז, למה שלא תתן שבוע חופש לקבוצה שלך מהגשת תרגילים (הכוונה לתרגיל 9 שעדיין לא פורסם), לקראת הבוחן שקרב ובא, וכך גם לא יווצר פער נוסף בהגשת התרגילים לקבוצה השנייה?

תשובה

זה אכן התכנון, תנו לנו קצת קרדיט.

שאלה

יכול להיות שבשאלה 5 (תרגיל 8) בהגדרה של rn, בסיגמה k צריך לרוץ רק עד n-1? תומר טקסט מודגש - נכון , זה מה שצריך להיות . יתוקן !

שאלות

1. בתרגיל 8, שאלה 3 - נניח שיש לי פונקצייה רציפה f, אזי יש לה קדומה F. אפשר להסיק שגם ל-F יש קדומה (כי היא גזירה, ולכן רציפה), נכון?

2. בשאלה 4 - האם הגיוני שהתשובה שלי תכלול 2-3 שורות? (כשאני מנמק)

תשובה

יותר מזה, האינטגרל מאפס עד x של כל פונקציה אינטגרבילית הוא פונקציה רציפה ולכן יש לו קדומה.

לא יודע, התשובה הנכונה אכן לא ארוכה מידי, צריך לוודא שאתה מציין את כל הפרטים החשובים.

תרגיל 8

בשאלה 6, יכול להיות שהנתון גזירה ברציפות מיותר? לא מספיק להניח שהיא רק רציפה ב- [a,b]? (זאת מסקנה ישירה מהנתון על הגזירות, אבל האם כל השאר באמת הכרחי?)

תומר - אגלה לך רמז ואל תגלה לאף אחד ! - בעיקרון מספיק להניח שהפונקציה "רק" אינטגרבילית , אבל אז ההוכחה לטענה קצת יותר מורכבת . אבל לך על זה ! :) - מה אמרת לגבי "מסקנה ישירה מהגזירות " ? - ראינו שהתנאי שפונקציה גזירה , לא אומר שנגזרתה רציפה , ובטח לא אומר שנגזרתה אינטגרבילית ...

לדעתי מספיק להניח שהיא רציפה בקע, לכן היא אינטגרבילית שם וחסומה, וההמשך ע"י הסנדוויץ'... לא? זה הפתרון המסובך?

תומר - לא מגלה ...:) יכול להגיד שלפי הנתון בשאלה , ההוכחה היא די פשוטה . בהמשך אפרסם לכם הוכחה למקרה הכללי , כשהפונקציה רק אינטגרבילית ! תומר - שוב אני . ראה , כשאתה אומר "לדעתי " - תן לדיעה הזו נימוק מתמטי או - מצא בסופו של דבר שזה לא נכון . אין הגיון כאשר אתה עוד בשלב ה"לדעתי " - שאני אפסול לך את הכיוון או אאשר אותו ,כי אתה צריך לבנות אינטואיציה ולהוכיח אותה או להפריך מתמטית . עדיף לך (!) שלא אכוון אותך בשלב זה , אלא ש"תתלכלך " קצת עם ניר ועיפרון . אמרתי לכם שעוד תודו לי יום אחד :) בהצלחה !

תרגיל 8

בשאלה 1 b כיצד אפשר לדעת משהו על התחום בין Pi/2 ל-Pi?

תשובה

צודק, יש טעות בשאלה, אני מיד מעלה תיקון

שאלה - הבוחן הקרוב

לארז ותומר - יש לי בקשה קטנה אליכם, אתם לא חייבים להיענות לה אבל בבקשה תקראו אותה: בסמסטר הקודם הבוחן בלינארית אמנם לא היה קשה בצורה רצחנית, אבל שאלת ההוכחה יחד עם כמה שאלות טריקיות הביאו למצב שהממוצע שלו היה די נמוך, ולא מעט תלמידים ששפרו משמעותית את ציוניהם במבחן הסופי נאלצו לאבד מספר לא מבוטל של נקודות. בקורס אינפי 1 הסיפור דומה, רק שכאן הציונים בבוחן היו נמוכים כ"כ, וכן התרגילים שהגשנו לא נבדקו בזמן, עד שהוחלט שהציון ייקבע באופן שונה מהצפוי. כמעט כולם בתוכנית הזו שואפים לציון כמה שיותר גבוה, והלב כואב כשאחרי שבועות של למידה למבחן הסופי מצליחים להוציא בו ציון גבוה, אך כתוצאה מהבוחן יורדות להן 4-5 נקודות.

לכולנו (יותר נכון ל-95% וקצת יותר מאתנו שלומדים בתיכון) יש עומס עצום, ובכל שלושה ימים יש בביה"ס מתכונת נוספת או בגרות כזו או אחרת. על כל חופש אפשרי שיש לנו ב"חגי ישראל" מצמידים מיד אחריו איזו מתכונת (למשל ל"ג בעומר, או שבועות), ונכון שאנחנו אמורים להתמודד עם העומס הזה, אבל אני בספק אם מישהו באמת מרגיש מוכן לבוחן, או שבאמת יהיה לו זמן (מלבד ארבעת הימים שלפני הבוחן - שישי, שבת, ראשון ושני) לחזור על כל החומר ולהבין באמת עד רמה של תרגילים לבוחן.

בתודה רבה, ואני מצפה לתגובה מכם, ומקווה שלכולנו יילך כמה שיותר טוב :)

תשובה

הציונים חשובים לכם וזה טוב מאדאבל אם כולם יקבלו 100 לציון לא תהיה משמעות רבה, נכון? בלינארית המבחן היה עם ממוצע גבוה במיוחד (אפשר לדבר על הסיבות, אני חושב שהיה שילוב של מבחן לא מסובך וסטודנטים שידעו את החומר). אין לנו מטרה לעשות בוחן מכשיל שיוריד נקודות במכוון, אך הוא כן צריך להיות ברמה מספקת.

אני אגלה סוד מקצועי, מבחן טוב הוא מבחן עם ממוצע 70. מכיוון שאתם תלמידים טובים, אפשר גם לכוון לממוצע 80. כך היה בבוחן בלינארית 1, הממוצע שלו לא היה נמוך בכלל. הבוחן הוריד לכם נקודות כי המבחן היה עם ממוצע גבוה מידי. כמובן שאנו לא נותנים שאלות קשות במיוחד על מנת להוריד אתכם ל80, אבל זה המצב באופן טבעי כאשר נותנים שאלות הוגנות (בכל זאת אתם לא גאונים בחמש רמות מעל כל שאר תלמידי המתמטיקה בעולם).

ארז, אני לא בטוח שהיה בוחן בלינארית אחד.

שאלה - תרגיל 8

בתרגיל 8, בשאלה 7 - בסעיף הראשון, האם מותר להסתמך על קיומה של פונקצייה קדומה ל-f, ורק להראות שנגזרת כזו קיימת לפי כללי נגזרת? (ולא לפי הגדרת הנגזרת שכוללת גבולות)

תשובה

כן

שאלה

כשמבקשים ממני למצוא גבול של סדרה (כמו בשאלה 5 - בתרגיל 7). נניח לקחתי את הקטע [0,1] ואני רוצה לחלק אותו לn קטעים שווים. יש רק דרך אחת לחלק אותו.. לא? כלומר אני לוקחת רק חלוקה אחת כזו?

תשובה

ההגדרה של אינטגרביליות לפי רימן אומרת שלכל חלוקה עם פרמטר חלוקה מספיק קטן, סכום הרימן קרוב לאינטגרל המסויים עד כדי אפסילון.

אני לא בטוח מה כוונת השאלה בדיוק, אבל את הקטע אפשר לחלק בהרבה דרכים. דרך אחת תוביל לפתרון התרגיל.

אם למשל n=4. יש רק דרך אחת לחלק את הקטע [0,1] לn קטעים לא? (זאת שאלתי.)

ועוד שאלה. בנוגע לאינטגרציה בהצבה - באינטגרל מסוים. למדנו את המקרה כאשר ההצבה היא x=g(t). אך מה קורה כאשר t=g(x)? מהם גבולות האינטגרציה??

בוודאי שלא, מי אמר שהחלקים צריכים להיות שווים? למשל חלק באורך חצי ושלושה חלקים באורך שישית, או ארבע חלקים באורך רבע וכו'.

סליחה - התכוונתי לn חלקים שווים :-) אז זו בעצם דרך החלוקה שאבחר בשאלה על מנת להתאים את האיבר הכללי לסכום רימן.

לא כדאי להסתבך יותר מידי עם התרגיל הספציפי הזה אבל...

דיברנו כבר על העניין הזה. ההצבה ההפוכה היא למעשה הצבה מהאינטרגל החדש בחזרה לישן, וכך אפשר גם להבין מה יהיה גבולות האינטגרציה. (בכל מקרה מסתכלים על התחום של המשנה הידוע, ורואים באיזה תחום נמצא המשתנה החדש).

פתרונות

היי תומר/ארז. תרגילים 7 ו8 כלולים בחומר של הבוחן.. אני מודע לכך שקבוצה אחת לא תגיש את תרגיל 7 עד הבוחן ואולי אף שתי הקבוצות לא יגישו את 8?.. אבל תוכל בבקשה להעלות את הפתרונות שלהם לקראת הבוחן? זה חשוב.

שאלה קטנה

ב1a (תרגיל 7). החלק הראשון של ההוכחה טריוויאלי לא? פשוט 'הראיתי' (טריוויאלי כשלעצמו - בדקתי בקצוות) שg(x)=f(y) כאשר g בתחום a-alpha, b-alpha וf בתחום a,b..

תשובה

האם בדיקה בקצוות מוכיחה שהפונקציה אינטגרבילית?

לא. אבל הראיתי שהפונקציות שוות על ידי בדיקה בקצוות.. (זה טריוויאלי.. אני לא ממש יודעת איך להראות את זה בדרך אחרת..)

הפונקציות בוודאי לא שוות. הן מקבלות את אותם הערכים בקטעים השונים. אפשר להראות את זה בעזרת הגדרת האינטגרל המסוים לפי סכומי רימן.

תרגיל 8

בשאלה 1 a, האם מספיק להצביע על טעות אחת שעשה דני? או שצריך להראות את כולן?

תשובה

צריך לעלות על הנקודה העיקרית, סעיף ב' קצת עוזר להבין את זה אני חושב.

שאלה

אני חושב שהשאלה הזו נשאלה פה כבר בעבר.. אבל לא בדיוק הבנתי. אם נתון לי שf(x)>0 (כלומר, גדול ממש) אז גם האינטגרל שלו גדול ממש? או למשל f(x)>g(x).. זה אומר שהאינטגרל גדול ממש?

ועוד שאלה.. כדי להשתמש בנוסחה של אורך עקומה של פונקציה צריך לדרוש שהפונקציה תהיה רק גזירה (כמו שכתוב בדף העזר שהועלה לאתר) או גזירה ברציפות?

ועוד שאלה קטנה :P אם פונקציה רציפה ב[a,b] וב[b,c], אפשר לומר שהיא רציפה ב[a,c]?

תשובה

הםונקציה גדולה מאפס בכל הקטע? אם כן היא רציפה (לפי לבג) בנקודה כלשהיא, ולכן בסביבת דלתא שלה היא גדולה מאיזה ערך חיובי ולכן האינטרגל שלה גדול מערך חיובי כפול דלתא ולכן גדול ממש מאפס.

נניח כרגע גזירה ברציפות, אני אבדוק אם אפשר להניח פחות

כן כי הגבול שלה משמאל ומימין בנקודה b הוא הערך של הפונקציה בנקודה b ולכן גם הגבול בנקודה

תודה רבה

הבוחן

מומלץ לעבור שוב על הוכחות המשפטים מההרצאה לקראת הבוחן, או שהדגש יהיה על יישום כפי שעשינו בתרגול? כלומר, הבוחן יכלול שאלות תיאורטיות, מעשיות, או גם וגם? הוכחות או חישובים? תודה. תומר - נכתוב את הבוחן בימים הקרובים וניידע אתכם בהקדם האפשרי. עם זאת יש שאלות "תיאורטיות" שאינן הוכחת משפט אלא למשל "הוכח או הפרך " ...

צריך לדעת חקירת פונקציות? כי לפי מה שהבנתי זה לא ממש בסילבוס הקורס..

כל מה שלומדים זה חלק מהקורס.

שאלה כללית

איך אני מוכיח שלפונ' לא קיימת קדומה? פשוט המרצה נתן דוגמא לפונ': 1 כשX>0 ו1- כשX<=0 ואמר שלא קיימת לה קדומה, ואני גם חושב שהוא אמר שאם לא היינו מגדירים אותה ב0, היה לה קדומה והיא |X|. אז יש לי 2 שאלות: 1) איך הוא ידע שאין לה קדומה? 2) אם היא אינה מוגדרת ב0, היא בכלל לא פונ'? (או שאני טועה, לדוגמא, האם y=1/x אינה בכלל מוגדרת כפונ' כי היא לא מוגדרת ל0?) בכל מקרה, אשמח אם מישהו יסביר לי את מקור הבלבול. תודה!

(לא תומר/ארז). לפונקציה שקיימת לה קדומה (כלומר, היא נגזרת של פונקציה אחרת) יש נק' אי רציפות רק מסוג שני..

אני לא מבין למה. זה משפט?

כן זה משפט. זה נובע ממשפט ערך הביניים על נגזרות

אבל אם לא היינו מגדירים את הפונקציה ב-0, עדיין הייתה לה ב-0 נקודת אי רציפות ממין ראשון, ובכל זאת הייתה לה קדומה...

תומר - חברים , אני ניסחתי לכם את המשפטים המתאימים הקשורים לתכונות הנגזרת ( תכונת ערך הביניים והעובדה שנקודות אי רציפות של נגזרת הן מסוג שני בלבד ) . כדי שתוכלו להתרשם יותר מהמשפטים עצמם - אכתוב לכם את הוכחתם ואפרסם כאן באתר - אני מקווה שקריאת הוכחתם תעשה יותר סדר בעניין . כרגע חשוב שתבינו את התכונות האלו אפילו בלי הוכחתן .

מישהו אחר: אני אחדד את השאלה הקודמת, גם אני מתקשה בזה: האם יש קריטריון שאומר איזו פונקצי היא בעלת קדומה ואיזו פונקציה אינה בעלת קדומה? כלומר, אמרנו שכל הפונקציות שיש להם קדומה אז אם יש להן אי רציפות זה ממין שני. אבל יש פונקציות שיש להן נקודות אי רציפות ממין שני ובכל זאת אין להן קדומה? ותומר- לא ראיתי שענית- אם את הפונקציה שהוא הגדיר למעלה לא היינו מגדירים באפס, אז היה לי אי רציפות ממין ראשון ובכל זאת הייתה לה קדומה....

תודה רבה!

תומר - הממ , לגבי הפונקציה עם הקפיצה - יש לה קדומות בתחומי הגדרה שונים שלה - למשל לx>0 בנפרד , ולשליליים בנפרד - אבל להגיד שיש קדומה הכוונה כל תחום הגדרתה . וזה לא לא מתקיים בגלל אי הרציפות באפס שלא משנה איך תגדיר את הפונקציה באפס - לא תוכל לגשר על הפער של הקפיצה בה ("אי רציפות מסוג ראשון " ) . לגבי אחד חלקי איקס - אם נגדיר את ערכה באפס להיות מינוס 3 למשל , עדיין היא תהיה לא חסומה עבור הקטע [0,1] , ולכן לא אינטגרבילית רימן . היום אנו מכירים אינטגרל לא אמיתי וניתן להתייחס אליה במובן זה ...

שאלה בנוגע לטורי טיילור

היי. קצת ישן אבל לא נורא.. בנוגע לטורי טיילור. אם אני רוצה למשל לפתח את הפונקציה e^(-x^2/2). האם אני צריכה להתייחס למשתנה כx? כלומר, ברור לי שהגזירה היא של e^(-x^2/2), אבל בנוסחת טיילור המשתנה עצמו הוא x והביטוי (x-x0) מופיע בחזקות שונות. אז האם במקרה הזה, זה (-x^2/2-x0) או (x-x0?) תודה מראש :)

(זה לא ארז/תומר) x-x0, כמובן...

שאלה

אני לא מבין איך עוד לא העלו את הנושא, כאילו, אני היחיד שסובל? השיעורי בית ק ש י ם. אני עשיתי חזרה על ההרצאות, עשיתי חזרה על התרגולים בכיתה, והקשר מבחינת הרמה בינם ובין השיעורי בית (תרגילים 7,8) מקריים בהחלט. אני אפילו לא יודע איך להתחיל אותם. זה לא הגיוני שאני יושב כבר 4 שעות על דף של שיעורי בית ולא מצליח אפילו תרגיל אחד בלי להתקשר למישהו. זה אומר שאני מטומטם? XD

מסכים בכל לבי.

מסכימה לגמרי.. הקשר בין התרגולים לש.ב בהחלט מקרי

מסכים בלב מיואש... ואני לא רוצה כבר לבקש עזרה מאחרים - לא כי לא נעים לי, אלא כי אני מרגיש שאני אידיוט אם אני לא מסוגל להתמודד עם זה לבד (וחרשתי על מייזלר, על כמה עשרות עמודים ועל המון דוגמאות).

תשובה

הקשר בין תרגילי השיעור לתרגילי הבית הוא שעליכם להבין מה שנעשה בשיעור וליישם אותו על תרגילים שונים בבית. אתם באמת חושבים שהייתם מסתדרים יותר טוב אם היינו פותרים את תרגילי הבית בכיתה, ואת תרגילי הכיתה משאירים הבייתה? כנראה שלא...

תרגילי הבית נלקחים בחלקם הגדול מתרגילים של קורסים מקבילים באוניברסיטת תל אביב. למעשה הם מקבלים תרגילים ארוכים יותר, ואנחנו מקצרים אותם.

מסקנה: התרגילים מאתגרים, וטוב שכך. יש לכם את הכלים להתמודד איתם.

שאלה

האם יש בבוחן דף נוסחאות של האינטגרלים? תודה

שאלה

(השאלה מדברת על תרגיל 8 בלבד) בתרגיל 1 סעיף ב', הגדרתם את F,G להיות אינטגרלים לא מסויימים, שזה קצת מוזר. זה לא טעות? ועוד שאלה: בתרגיל 2, הניסוח של משפט ערך הביניים בבן ציון מופיע כך: "תהי F רציפה ב[a,b], ויהי y0 מס' ממשי בין f(a),f(b) אז קיימת נק' a<x0<b כך שf(x0)=y0. זה לא עושה את התרגיל טריויאלי?

תשובה

בהנתן פונקציה קדומה, קל לחשב את האינטגרל המסוים (אם הוא קיים).

כמובן שלא אמורים להסתמך על משפט שאומר אותו דבר, אלא להוכיח את התרגיל מאפס (אין צורך להשתמש באף גרסא של משפט ערך הביניים)

שאלה

בקשר להצבות. כשמדובר על אינטגרל מסוים, תמיד דורשים שהפונקציה שאנו מציבים תהיה הפיכה וגזירה. אבל כשמדובר על אינטגרל לא מסוים, מהן הדרישות בדיוק? אודה מאוד אם ארז/תומר יוכלו להבהיר את הנקודה..

תשובה

קודם כל אני מציע שתקרא בתשובות קודמות כי כבר ענינו על הנקודה הזו. אין הכרח תמיד שהפונקציה תהיה הפיכה בהצבה. צריך להבין מהו מקרה ההצבה הספציפי, הכל נובע מהנוסחא 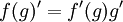$f(g)'=f'(g)g'$. צריך להבין איך להגיע לנוסחא הנ"ל במקרה הנתון, לפעמים צריך לגזור, לפעמים צריך להפוך ולגזור.

בכוונה שאלנו את השאלה עם דני על מנת שתחשבו בעצמכם מה ההצבה אומרת ולא תנסו סתם לשנן כללים.

כן, אז חשבתי שברגע שמציבים x=f(t) דורשים גזירות וגם הפיכות. אבל לפי השאלה של דני, גם במקרה השני של t=f(x), דורשים הפיכות!

תלוי במקרה הספציפי!

הסתכלתי בארכיון. אבל שם אתה מדבר רק על הצבות מהסוג u=g(x). מה עם הצבות מהסוג x=g(t)??

הכל אותו רעיון. אתה חייב להגיע לאינטגרל של נוסחא 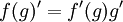$f(g)'=f'(g)g'$, יכול להיות שתצטרך להשתמש בהופכית על מנת להגיע לנוסחא הזו. תוכל לראות את הפתרון המדויק לתרגיל מחר בערב.

שאלה

כדי להוכיח רציפות לא מספיק להראות שהגבולות מימין ומשמאל לנק' שווים, צריך גם להראות שהם שווים לערך בנקודה. אבל כשאנחנו רוצים להוכיח (כמו בתרגיל 4 למשל) שלפונקציה מסוימת (שמחולקת לקטעים) יש קדומה, אנחנו רק דורשים שיוויון של הגבולות מימין ומשמאל. למה זה מספיק?

תשובה

אני לא בטוח לאיזו שאלה בתרגיל 4 אתה מתכוון. בכל אופן אם הגבולות קיימים משמאל ומימין אבל לא שווים לערך בנקודה זו אי רציפות סליקה או ממין ראשון. ולכן בוודאי אין פונקציה קדומה (כי לנגזרת יש הכי הרבה אי רציפות ממין שני).

לכן כן יש להוכיח שהגבולות החד צדדים שווים לערך בנקודה על מנת להראות שלפונקציה יש קדומה (לאינטיגרביליות הערך בנקודה מסויימת אינו קריטי).

התכוונתי לשאלה 2. בפתרונות שהעלתם.. הבדיקה היא רק של הגבולות מימין ומשמאל..

לא רשום במפורש שנעשתה הבדיקה, אבל כן רשום במפורש (ועם קו תחתון) שהפונקציה שקיבלנו רציפה. לא תמיד אנחנו רושמים את כל הפרטים, יש חלקים שצריך להשלים לבד. כמובן שבכדי שהפונקציה תהא רציפה הערך בנקודה חייב להיות שווה לגבול בנקודה.

שאלה

בתרגיל 8 שאלה 2, האם מותר להשתמש במשפט הערך הממוצע, ואז להראות שזה פשוט לא יכול להיות a או b?

תשובה

לא כי זה פשוט לא נכון. קח את הפונקציה הקבועה. קח פונקציה אחרת שבמקרה מקבלת את הממוצע בקצוות...

שאלונת

האם אינטגרביליות של פונקציה בקטע [a,b] גוררת קיום של פונקציה קדומה בקטע זה? (ברור לי שההפך לא נכון, אבל בקשר לכיוון הזה אני לא בטוחה..)

תשובה

בוודאי שלא, כי יכול להיות שהאינטגרבילית מכילה אי רציפות סליקה או ממין ראשון ולכן אין לה קדומה. למשל פונקציה קבועה עם קפיצה בנקודה אחת, אין לה קדומה.