שיחה:89-214 הדרכות והסברים
תוכן עניינים
תרגיל 5
5.3.9
הבהרה לגבי חבורת קיילי (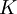 ) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של
) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של 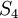 . אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך.
. אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך.
5.3.13
היכנם מתבקשים להראות מצד אחד שהליבה היא תת-חבורה נורמלית, ומצד שני שהיא מקסימלית ביחס להכלה מבין כל תתי-חבורות הנורמליות של 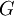 שמוכלות ב
שמוכלות ב 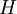 . זאת אומרת, לכל תת-חבורה
. זאת אומרת, לכל תת-חבורה 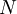 נורמלית של
נורמלית של 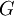 שמוכלת ב
שמוכלת ב 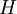 , מתקיים
, מתקיים 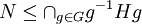
שאלה: אתם יכולים לתת דוגמא לאיך האיברים בליבה ניראים? אם יש לנו נגיד 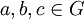 אז זה חיתוך של
קבוצה שנראית ככה:
אז זה חיתוך של
קבוצה שנראית ככה:
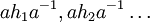 עם קבוצה שנראית ככה:
עם קבוצה שנראית ככה:
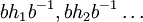 וכו'.
וכו'.
תשובה: איבר היחידה הוא בליבה. מעבר לזה - אין צורך לדעת לצורך פתרון של השאלה. בסה"כ הבנת את ההגדרה נכון.
שאלה קטנה נוספת: אז לא צריך להוכיח שהיא תת חבורה? רק נורמליות ואז להראות מקסימליות?
תשובה לשאלה הקטנה: צריך. שים לב שההוכחה לוקחת בערך שורה.
5.3.11
הכוונה היא לחבורה שנוצרת על ידי הקבוצה 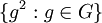 . זאת אומרת אוסך כל המכפלות הסופיות מהצורה
. זאת אומרת אוסך כל המכפלות הסופיות מהצורה 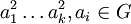 . אין צורך להוכיח זאת בתרגיל, אבל תבדקו עם עצמכם שאתם מבינים מדוע זו חבורה בכלל. עליכם להראות שחבורה זו נורמלית.
. אין צורך להוכיח זאת בתרגיל, אבל תבדקו עם עצמכם שאתם מבינים מדוע זו חבורה בכלל. עליכם להראות שחבורה זו נורמלית.
5.3.14
לשאלת התלמידים ששאלו איך לפתור את סעיף ג' - הרעיון הוא להשתמש בסעיף א. כיצד הראתם נורמליות של
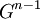 ?
?
שימו לב שמדובר ב-n נתון מראש. בנוסף - יש להראות ש 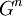 היא תת-חבורה של
היא תת-חבורה של 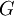 . בסעיף א' ובכל שאר הסעיפים מדובר באותו n שמופיע בנתון.
. בסעיף א' ובכל שאר הסעיפים מדובר באותו n שמופיע בנתון.